Fécondité par cohorte et période
Description de la méthode
La disponibilité de données démographiques détaillées et d’histoires génésiques recueillies dans des enquêtes démographiques (comme l’Enquête mondiale de fécondité dans les années 1970 et le programme en cours des Enquêtes démographiques et de santé organisé par ORC Macro) a conduit à préférer généralement les mesures directes d’estimation de la fécondité aux mesures indirectes. Toutefois, l’extension de méthodes indirectes à des situations où des données détaillées existent peut non seulement offrir le moyen de corroborer les résultats obtenus directement mais aussi fournir des informations importantes sur la qualité des données recueillies grâce aux histoires génésiques.
Une de ces extensions consiste à appliquer aux histoires génésiques la logique de la méthode du quotient P/F de Brass, et à conduire ainsi une étude détaillée des données de fécondité par âge, période et cohorte. La méthode permet d’obtenir des estimations de l’indice synthétique de fécondité (TF, total fertility) pour une ou deux périodes de cinq ans précédant la collecte des données. Elle permet aussi d’identifier des erreurs courantes dans les données.
Données nécessaires et hypothèses
Tableaux de données nécessaires
- Nombres de femmes par groupe d’âge à la date d’enquête
- Nombres de naissances par groupe d’âge (actuel) de la mère, par période de cinq ans avant l’enquête. L’élaboration de ce tableau nécessite, pour chaque enregistrement dans une histoire génésique,
- la date (mois et année) de l’interview ;
- la date (mois et année) de naissance de l’enfant ; et
- le groupe d’âge actuel de la mère.
Hypothèses
Il n’y a pas de différence de fécondité entre les femmes interrogées dans l’enquête et celles qui ne l’ont pas été parce qu’elles sont décédées ou ont émigré.
Travail préparatoire et recherches préliminaires
On peut appliquer la méthode en travaillant avec les procédures de traitement des dates disponibles dans la plupart des logiciels statistiques, ou (presque aussi bien) en utilisant les dates dans le format CMC des EDS (en mois à partir du début du 20ème siècle). Si les dates de naissance et d’interview n’ont pas été codées ainsi, nous recommandons de le faire pour appliquer la présente méthode. La procédure est décrite ici.
Application de la méthode
L’application de la méthode se fait selon les étapes suivantes.
Etape 1 : Déterminer le nombre (pondéré) de femmes par groupe d’âge à la date d’enquête
Le tableau est construit aisément. Avec les données des EDS, la variable v013 donne le groupe d’âge des femmes, et v005 (divisé par 106 si nécessaire) les pondérations de l’échantillon. On désigne par Ni = 5Nx le nombre de femmes dans le groupe d’âge i, avec x = 15, 20…, 45 et i=x/5-2.
Etape 2 : Déterminer les nombres de naissances par groupe d’âge et période avant l’enquête
Si on travaille avec des dates au format CMC, avec une histoire génésique complète dans un fichier avec un enregistrement par enfant, l’âge actuel de l’enfant est facilement calculé en retranchant le CMC de sa date de naissance du CMC de la date d’interview. En divisant le résultat par 60 et en prenant la partie entière du résultat on obtient un index qui permet d’allouer la date de naissance de l’enfant à l’une des périodes quinquennales antérieures à l’enquête.
Une modification minime est nécessaire dans les cas où l’enfant est né le même mois que l’interview, exactement 5ans, 10 ans, … auparavant. Selon la position respective du jour d’interview et du jour de naissance, les enfants peuvent être dans l’un ou l’autre des deux groupes d’âge adjacents. Pour résoudre ce problème et éviter de placer tous ces cas dans le même groupe, les enfants des mois-frontières doivent être alloués aux groupes d’âge en fonction de la date d’interview, si elle est connue, et en supposant que les jours de naissance sont répartis uniformément chaque mois. Quand c’est possible, nous définissons b =1 si le jour (au cours du mois calendaire) de l’interview < 16 – l’anniversaire de l’enfant étant alors plus vraisemblablement dans la seconde moitié du mois – et b =0 dans les autres cas.
Donc
(1)
où DoI est la date de l’interview et DoBc la date de naissance de l’enfant, toutes deux enregistrées en format CMC. Dans le cas des données EDS, DoI est fourni par la variable v008 et DoBc par la variable b3. Le jour d’interview est donné par la variable v016.
On construit ensuite un tableau croisé (pondéré, si nécessaire, pour tenir compte du plan d’échantillonnage) du groupe d’âge de la mère à la date d’enquête par un regroupement de la variable ‘moment de la naissance’ définie ci-dessus. La structure du tableau croisé est illustrée au tableau 1, où les Bij représentent le nombre agrégé (pondéré) d’enfants nés il y a j années de mères appartenant au groupe d’âge i à la date d’enquête :
Tableau 1 Structure des tableaux utilisés dans le calcul des taux de fécondité par cohorte et période
Groupe d’âge de la cohorte à l’enquête (i) |
Nombre de femmes | Naissances par période avant l’enquête (j) | ||||
|---|---|---|---|---|---|---|
0-4 (j=0) | 5-9 (j=1) | 10-14 (j=2) | 15-19 (j=3) | 20-24 (j=4) | ||
15-19 (i=1) | N1 | B1,0 | B1,1 |
|
|
|
20-24 (2) | N2 | B2,0 | B2,1 | B2,2 |
|
|
25-29 (3) | N3 | B3,0 | B3,1 | B3,2 | B3,3 |
|
30-34 (4) | N4 | B4,0 | B4,1 | B4,2 | B4,3 | B4,4 |
35-39 (5) | N5 | B5,0 | B5,1 | B5,2 | B5,3 | B5,4 |
40-44 (6) | N6 | B6,0 | B6,1 | B6,2 | B6,3 | B6,4 |
45-49 (7) | N7 | B7,0 | B7,1 | B7,2 | B7,3 | B7,4 |
Notez que, lorsqu’on remonte dans le temps, les taux de fécondité des femmes les plus jeunes sont nuls pour des périodes où toutes ces femmes ont moins de 10 ans. Certaines des naissances passées ne sont pas déclarées si les histoires génésiques ne sont recueillies qu’auprès des femmes âgées de moins de 50 ans.
Etape 3 : Calculer les taux de fécondité par cohorte et période fondés sur le groupe d’âge de la mère au moment de l’enquête
Si nous désignons les groupes d’âge (ou les cohortes définies par l’âge à l’enquête) par l’indice i (i = 1 correspondant au groupe 15-19 ans, etc.) et les périodes quinquennales successives antérieures à l’enquête par l’indice j (j = 0 correspondant à la période qui précède immédiatement l’enquête et se termine à la date de celle-ci), les taux de fécondité par cohorte et période sont définis par
Le rapport est divisé par cinq car les femmes sont exposées cinq ans exactement, toutes étant vivantes au long de chacune des périodes antérieures à l’enquête.
Les taux par cohorte et période mesurent la fécondité des femmes d’une même cohorte (nées au cours de la même période) en ligne, les périodes étant en colonne, et les âges atteints équivalents diminuant le long des diagonales (tableau 2).
Tableau 2 Taux de fécondité par cohorte et période, classés par âge de la cohorte à l’enquête
Groupe d’âge de la cohorte à l’enquête (i) | Taux de fécondité par période avant l’enquête (j) | |||||
|---|---|---|---|---|---|---|
0-4 (j=0) | 5-9 (j=1) | 10-14 (j=2) | 15-19 (j=3) | 20-24 (j=4) | ||
15-19 (i=1) | f1,0 | f1,1 |
|
|
| |
20-24 (2) | f2,0 | f2,1 | f2,2 |
|
| |
25-29 (3) | f3,0 | f3,1 | f3,2 | f3,3 |
| |
30-34 (4) | f4,0 | f4,1 | f4,2 | f4,3 | f4,4 | |
35-39 (5) | f5,0 | f5,1 | f5,2 | f5,3 | f5,4 | |
40-44 (6) | f6,0 | f6,1 | f6,2 | f6,3 | f6,4 | |
45-49 (7) | f7,0 | f7,1 | f7,2 | f7,3 | f7,4 | |
Etape 4 : Transposer les taux de fécondité par cohorte et période
Les taux obtenus à l’étape 3 peuvent aussi être classés par âge de la mère au terme de chacune des périodes quinquennales successives. Le terme de la période quinquennale précédant l’enquête (quand j = 0) est la date d’enquête, et le terme de la période 5-9 ans avant l’enquête (quand j = 1) est le point exactement cinq ans avant l’enquête. Ce reclassement a pour conséquence la création d’une série révisée d’indices de fécondité par cohorte :
f*k,j=fk+j,j
Avec ce reclassement, le tableau 2 ci-dessus est réorganisé en tableau 3 ci-dessous. Ainsi, la fécondité des femmes âgées de 30-34 ans à l’enquête au cours de la période 10-14 ans avant l’enquête (i.e. f4,2) est remaniée en fécondité des femmes qui étaient âgées de 20-24 ans dix ans avant l’enquête (f*2,2).
Tableau 3 Matrice des taux de fécondité par cohorte et période, après redéfinition de l’âge
Groupe d’âge de la cohorte à la fin de chaque période (k) | Taux de fécondité par période avant l’enquête (j) | |||||
|---|---|---|---|---|---|---|
0-4 (j=0) | 5-9 (j=1) | 10-14 (j=2) | 15-19 (j=3) | 20-24 (j=4) | ||
15-19 (k=1) | f*1,0 | f*1,1 | f*1,2 | f*1,3 | f*1,4 | |
20-24 (2) | f*2,0 | f*2,1 | f*2,2 | f*2,3 | f*2,4 | |
25-29 (3) | f*3,0 | f*3,1 | f*3,2 | f*3,3 | f*3,4 | |
30-34 (4) | f*4,0 | f*4,1 | f*4,2 | f*4,3 |
| |
35-39 (5) | f*5,0 | f*5,1 | f*5,2 |
|
| |
40-44 (6) | f*6,0 | f*6,1 |
|
|
| |
45-49 (7) | f*7,0 |
|
|
|
| |
A mesure qu’on remonte dans le temps, les périodes ont un nombre régulièrement croissant de valeurs manquantes pour les femmes âgées si les histoires génésiques n’ont pas été recueillies auprès des femmes de plus de 50 ans. Par exemple, f*6,3 désigne la fécondité qu’ont eue il y a 15-19 ans les femmes âgées de 40-44 ans quinze ans exactement avant la date d’enquête. A l’enquête, ces femmes seraient âgées de 55-59 ans et n’ont donc pas été concernées par la section des histoires génésiques d’une enquête EDS.
Etape 5 : Calculer des mesures de fécondité par cohorte
Soit Pk,j la fécondité cumulée par cohorte (c’est-à-dire le nombre moyen d’enfants déjà nés) de 15 ans à la fin du groupe d’âge k de la cohorte de femmes âgées de k au temps j. Donc :
Etape 6 : Calculer des mesures de la fécondité par période et deux estimations de l’indice synthétique de fécondité
Les mesures de fécondité par période sont des taux cumulés de fécondité au cours d’une période donnée. Nous désignons par Fi,j la fécondité cumulée jusqu’à l’âge i lors de la période j. Donc,
Notez que F7,0 est une mesure de l’indice synthétique de fécondité (TF) de la période cinq ans précédant immédiatement l’enquête. On peut supposer que cette estimation s’applique (approximativement) 2,5 ans avant la date d’enquête.
La plupart du temps, F7,1 ne peut pas être évalué directement, car il faudrait que les femmes aujourd’hui âgées de 50-54 aient été interrogées sur la fécondité qu’elles ont eue quand elles avaient 45-49 ans dans la période quinquennale se terminant cinq ans avant l’enquête. Mais la fécondité dans ce groupe d’âge est généralement très faible, et une estimation approchée de la fécondité dans la période 5-9 ans avant l’enquête peut être obtenue en faisant
.
En d’autres termes, nous supposons que f*7,1 = f*7,0 = f7,0. Si la fécondité décroît, l’estimation sera un peu trop basse, mais comme la fécondité est généralement très faible dans ce groupe d’âge, le biais sera sans importance.
Dans les populations où la fécondité est basse ou assez basse (moins de 3 enfants par femme), il est raisonnable de procéder de même pour la fécondité non mesurée des femmes âgées de 40-49 ans dix ans exactement avant l’enquête, car la fécondité à 40-44 ans y est suffisamment faible pour que de légères variations aient un impact négligeable sur l’indice synthétique estimé 10-14 ans avant l’enquête. Dans ce cas, nous supposons que f*7,2 = f7,0 et f*6,2 = f6,1 pour pouvoir écrire
.
Etape 7 : Calculer les quotients P/F
Nous pouvons calculer directement les quotients P/F à partir des résultats issus des étapes 5 et 6. Le quotient P/F applicable au groupe k à la période j est égal à
Par exemple, le quotient P/F pour les femmes âgées de 25-29 ans dans la période se terminant dix ans avant l’enquête est, avec k=3 et j=2 dans la formule ci-dessus,
Interprétation et diagnostics
Plusieurs interprétations importantes émergent de ces résultats.
1. Estimations de la fécondité par période
On a vu, à l’étape 6, comment deux estimations de la fécondité pouvaient être obtenues, applicables environ 2,5 et 7,5 ans avant l’enquête. On peut en déduire une évolution à court terme de la fécondité.
2. Interprétation des quotients P/F ratios et calendrier de la baisse de la fécondité
Les quotients P/F obtenus à l’étape 7 peuvent nous donner des informations sur la nature et le calendrier de la baisse de la fécondité, ainsi que sur les problèmes de qualité des données. La section de ce manuel consacrée à quotient P/F de Brass décrit les traits essentiels de la méthode.
Des quotients P/F de, ou très proches de, 1 à chaque âge dans une période donnée impliquent qu’il n’y a pas eu de variation de la fécondité, les mesures de la fécondité par période et par cohorte étant à peu près égales. Une baisse de la fécondité se traduit par une augmentation continue des quotients P/F au fil des âges une période donnée, à partir de valeurs proches de l’unité avant 25 ans. (Nous utilisons 25 ans comme limite car il est difficile pour la fécondité par cohorte et par période de différer sensiblement pour les cohortes les plus jeunes.) Ainsi, si les quotients par âge P/F sont à peu près constants dans une période avant l’enquête, j, mais qu’ils font apparaître une nette tendance en fonction de l’âge au cours de la période suivante plus proche de l’enquête, j - 1, on peut en déduire que la fécondité a commencé à baisser (à peu près) à la date séparant les deux périodes.
Une série de quotients P/F faibles au cours d’une période suivie ou précédée par une série de quotients beaucoup plus élevés indique un éventuel déplacement des naissances vers la période où les quotients sont bas et au détriment de la période où ils sont exagérément élevés. De même, une série de quotients P/F qui s’éloigne sans explication de la tendance générale le long d’une diagonale (c’est-à-dire pour une cohorte particulière) suggère une mauvaise déclaration des âges par les femmes ou des omissions de naissances si la tendance est observée aux âges avancés.
3. Evaluation de la qualité des données
L’examen des taux de fécondité par cohorte et période (les f*) calculés à l’étape 4 peut contribuer à l’évaluation de la qualité des données. Par exemple, la lecture de droite à gauche le long des lignes montre comment évolue la fécondité de chaque groupe d’âge à mesure que s’approche la date d’enquête.
En l’absence de facteurs exogènes importants, on s’attend à des variations progressives et régulières, et les écarts à ce schéma peuvent refléter des erreurs sur la période de référence ou d’autres omissions. Trois types d’erreurs sur la période de référence sont courants dans les données d’histoires génésiques rétrospectives recueillies par enquête.
Le premier type d’erreur a été signalé par Brass, selon qui les femmes âgées tendent à exagérer l’âge de leurs ainés en situant leurs dates de naissance trop loin dans le passé. Il en résulte une surestimation du niveau de la fécondité des périodes anciennes et une sous-estimation de la fécondité récente du fait du transfert des naissances de périodes relativement récentes vers des périodes plus anciennes, exagérant ainsi la baisse apparente de la fécondité. Les ‘effets de Brass’ sont caractérisés par des taux de fécondité par cohorte et période nettement plus élevés dans tous les groupes d’âge que ceux des cohortes un peu plus récentes aux mêmes âges. Ce décalage des naissances vers le passé a aussi pour conséquence une sous-estimation de la baisse de la fécondité dans les périodes récentes.
Le deuxième type d’erreur sur la période de référence a été identifié par Potter (1977). Selon lui, les femmes tendent à rapprocher les naissances anciennes de la date d’interview, mais à déclarer correctement les événements récents. Il en résulte une sous-estimation du niveau de la fécondité des périodes anciennes, des taux de fécondité récents correctement estimés et une surestimation de ceux de la période intermédiaire. Le modèle de Potter s’appuie sur deux propositions. La première : « la date d’un événement est mémorisée d’autant moins précisément qu’elle est ancienne. La seconde : si une histoire génésique est recueillie grâce à des questions sur les naissances vivantes dans l’ordre où elles sont survenues, la date qu’une femme attache à un événement autre que le premier est influencée par l’information qu’elle a déjà donnée sur l’événement précédent » (Potter 1977 : 341). Les ‘effets de Potter’ jouent davantage quand les histoires génésiques sont recueillies dans l’ordre où les naissances se sont produites plutôt que dans l’ordre inverse, de la plus récente vers la plus ancienne.
Un troisième type d’erreur résulte de l’omission systématique des enfants nés juste avant l’enquête, ou de leur décalage vers une période plus ancienne. Il s’agit généralement pour un enquêteur d’éviter de devoir poser des questions détaillées supplémentaires (par exemple dans un questionnaire anthropométrique) sur les plus jeunes enfants (le plus souvent ceux de moins de cinq ans). Ces erreurs ont été bien démontrées par Cleland (1996) et Schoumaker (2010, 2011). Du fait de ces omissions ou de ces décalages, la baisse de la fécondité juste avant l’enquête se trouve exagérée et les quotients P/F de cette période très récente font apparaître une baisse de la fécondité largement accentuée. Une partie de cette baisse peut être réelle, mais les analystes doivent être vigilants sur les effets éventuels de ce type d’omission ou de décalage.
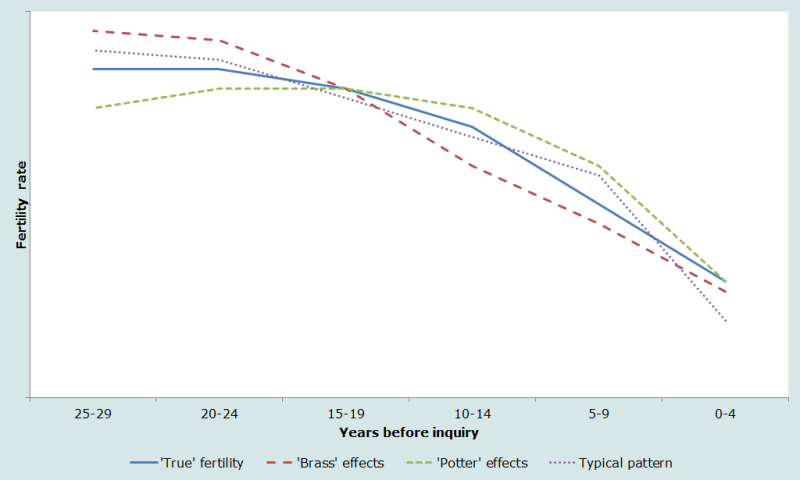
L’impact de ces trois effets sur les évolutions de la fécondité est illustré graphiquement sur la figure 1.
La courbe intitulée ‘fécondité réelle’ retrace l’évolution de la fécondité (totale ou par âge) au fil du temps dans une population hypothétique. Les effets de ‘Brass’ donnent l’impression d’une fécondité plus élevée pour le passé lointain et une baisse plus lente environ dans les 10 années précédant l’enquête. Les effets de ‘Potter’ entrainent une surestimation systématique de la fécondité au cours de 5-15 ans précédant l’enquête, donnant l’impression fausse d’une baisse récente plus rapide de la fécondité. Le ‘modèle typique’ indique la nature des distorsions fréquentes dans les données d’histoires génésiques. La fécondité de la période la plus récente est généralement trop basse, du fait de l’omission (dans les recensements) ou du décalage des naissances récentes pour éviter les modules complémentaires d’anthropométrie, etc. (dans les enquêtes), alors que la fécondité du passé très ancien est souvent surestimée (par le jeu des effets de ‘Brass’) et se marque par un excès apparent des naissances chez les très jeunes femmes dans de nombreuses histoires génésiques.
Exemple
Notre exemple s’appuie sur les données d’histoires génésiques rétrospectives recueillies lors de l’EDS du Malawi en 2004. Les tableaux ont été pondérés grâce aux poids d’échantillonnage fournis avec les données, ce qui explique les décimales dans les tableaux d’effectifs. La méthode est mise en application dans un dossier Excel joint.
Etapes 1 et 2 : Extraction des données
Les tableaux tirés des fichiers de données de l’EDS sont illustrés par le tableau 4. Les naissances déclarées par période antérieure à l’enquête ont été ajustées pour tenir compte approximativement du problème de frontière évoqué lors de l’établissement de l’équation 1.
Tableau 4 Nombre de femmes par groupe d’âge à l’enquête, et nombre de naissance de ces femmes par période de naissance, Malawi, EDS 2004
Groupe d’âge de la cohorte à l’enquête | Années de naissance approximatives de la cohorte | Nombre | Naissances par période avant l’enquête (j) | ||||||
|---|---|---|---|---|---|---|---|---|---|
0-4 (j=0) | 5-9 (j=1) | 10-14 (j=2) | 15-19 (j=3) | 20-24 (j=4) | 25-29 (j=5) | 30-34 (j=6) | |||
15-19 (i=1) | 1985-1989 | 2 392,0 | 713,7 | 5,2 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 |
20-24 (2) | 1980-1984 | 2 869,7 | 3 638,8 | 981,8 | 28,7 | 0,0 | 0,0 | 0,0 | 0,0 |
25-29 (3) | 1975-1979 | 2 157,4 | 2 952,3 | 2 693,6 | 859,1 | 13,6 | 0,0 | 0,0 | 0,0 |
30-34 (4) | 1970-1974 | 1 478,0 | 1 734,4 | 2 152,7 | 1 996,7 | 595,5 | 21,9 | 0,0 | 0,0 |
35-39 (5) | 1965-1969 | 1 116,8 | 1 139,6 | 1 462,6 | 1 815,5 | 1 386,4 | 508,4 | 18,1 | 0,0 |
40-44 (6) | 1960-1964 | 935,0 | 569,3 | 923,5 | 1 372,6 | 1 456,2 | 1 267,8 | 386,4 | 13,4 |
45-49 (7) | 1955-1959 | 749,1 | 235,1 | 558,8 | 952,6 | 1 024,9 | 1 128,3 | 953,3 | 311,6 |
Etape 3 : Calculer les taux de fécondité par cohorte et période classés par groupe d’âge de la mère au moment de l’enquête
Le tableau 5 présente les taux de fécondité par cohorte et période tirés des données du tableau 4. Par exemple, le taux de fécondité par cohorte associé aux naissances survenues 5-9 ans avant l’enquêtes chez les femmes âgées de 20-24 ans à l’enquête est égal à
(1/5).(981,8/2 869,7)=0,068.
Tableau 5 Taux de fécondité par cohorte et période, classés par groupe d’âge à l’enquête, Malawi, EDS 2004
Groupe d’âge de la cohorte à l’enquête | Période avant l’enquête (j) | ||||||
|---|---|---|---|---|---|---|---|
0-4 (j=0) | 5-9 (j=1) | 10-14 (j=2) | 15-19 (j=3) | 20-24 (j=4) | 25-29 (j=5) | 30-34 (j=6) | |
| 15-19 (i=1) | 0,060 | 0,000 |
|
|
|
|
|
20-24 (2) | 0,254 | 0,068 | 0,002 |
|
|
|
|
25-29 (3) | 0,274 | 0,250 | 0,080 | 0,001 |
|
|
|
30-34 (4) | 0,235 | 0,291 | 0,270 | 0,081 | 0,003 |
|
|
35-39 (5) | 0,204 | 0,262 | 0,325 | 0,248 | 0,091 | 0,003 |
|
40-44 (6) | 0,122 | 0,198 | 0,294 | 0,311 | 0,271 | 0,083 | 0,003 |
45-49 (7) | 0,063 | 0,149 | 0,254 | 0,274 | 0,301 | 0,255 | 0,083 |
Etape 4 : Transposer les taux de fécondité par cohorte et période
Les taux du tableau 5 sont transposés de sorte que les lignes représentent les âges atteints équivalents à la fin de chacune des périodes en colonne. Par exemple, une femme âgées de 30-34 ans à l’enquête était âgée de 25-29 ans à la fin de la période 5-9 ans avant l’enquête (et de 20-24 ans à la fin de la période 10-14 ans avant l’enquête), et ces taux de fécondité par cohorte (0,291 et 0,270 au tableau 5) sont maintenant classés à 25-29 et 20-24 ans respectivement (tableau 6).
Tableau 6 Taux de fécondité par cohorte et période, classés par âge de la mère à la fin de chaque période avant l’enquête, Malawi, EDS 2004
Groupe d’âge de la cohorte à la fin de chaque période avant l’enquête, | Période avant l’enquête (j) | ||||||
|---|---|---|---|---|---|---|---|
0-4 (j=0) | 5-9 (j=1) | 10-14 (j=2) | 15-19 (j=3) | 20-24 (j=4) | 25-29 (j=5) | 30-34 (j=6) | |
| 15-19 (k=1) | 0,060 | 0,068 | 0,080 | 0,081 | 0,091 | 0,083 | 0,083 |
20-24 (2) | 0,254 | 0,250 | 0,270 | 0,248 | 0,271 | 0,255 |
|
25-29 (3) | 0,274 | 0,291 | 0,325 | 0,311 | 0,301 |
|
|
30-34 (4) | 0,235 | 0,262 | 0,294 | 0,274 |
|
|
|
35-39 (5) | 0,204 | 0,198 | 0,254 |
|
|
|
|
40-44 (6) | 0,122 | 0,149 |
|
|
|
|
|
45-49 (7) | 0,063 |
|
|
|
|
|
|
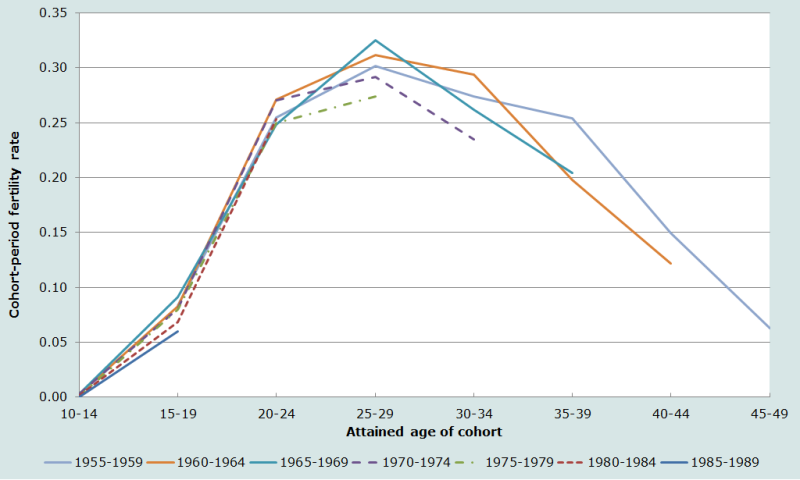
Pour faciliter l’identification des tendances de la fécondité et des problèmes ou des déficiences dans les données, on a représenté graphiquement (figure 2) les taux de fécondité par cohorte et période du tableau 6, par cohorte de naissance et âge atteint. Des omissions apparaissent systématiquement dans la fécondité des périodes les plus anciennes : les taux de fécondité par cohorte et période des femmes les plus âgées (la cohorte 1955-59) aux jeunes âges atteints (20-24 ans) sont plus faibles que ceux des cohortes un peu plus jeunes. Ces données révèlent néanmoins des signes d’un début de baisse de la fécondité au Malawi, les taux de fécondité dans les cohortes les plus jeunes (nées après 1980) étant plus faibles que ceux des cohortes plus âgées.
La dissociation de ces effets nécessiterait des recherches plus approfondies.
Etape 5 : Calculer des mesures de fécondité par cohorte
La fécondité par cohorte cumulée jusqu’à un âge donné est calculée en additionnant les taux par cohorte le long de la diagonale du tableau 6 et en multipliant par 5 (tableau 7). Par exemple, la fécondité cumulée des femmes âgées de 25-29 ans à la fin de la période 5-9 ans avant l’enquête est égale à 5.(0,291 + 0,270 + 0,081) = 3,210.
Tableau 7 Fécondité cumulée des cohortes à la fin de chaque période (P), Malawi, EDS 2004
Groupe d’âge de la cohorte à la fin de chaque période avant l’enquête, | Période avant l’enquête (j) | ||||||
|---|---|---|---|---|---|---|---|
0-4 (j=0) | 5-9 (j=1) | 10-14 (j=2) | 15-19 (j=3) | 20-24 (j=4) | 25-29 (j=5) | 30-34 (j=6) | |
| 15-19 (k=1) | 0,298 | 0,342 | 0,398 | 0,403 | 0,455 | 0,413 | 0,416 |
20-24 (2) | 1,610 | 1,647 | 1,754 | 1,697 | 1,769 | 1,689 |
|
25-29 (3) | 3,015 | 3,210 | 3,322 | 3,327 | 3,195 |
|
|
30-34 (4) | 4,384 | 4,632 | 4,795 | 4,563 |
|
|
|
35-39 (5) | 5,652 | 5,783 | 5,835 |
|
|
|
|
40-44 (6) | 6,391 | 6,581 |
|
|
|
|
|
45-49 (7) | 6,895 |
|
|
|
|
|
|
Etape 6 : Calculer des mesures de la fécondité par période et deux estimations de l’indice synthétique de fécondité
La fécondité cumulée par période jusqu’à un âge donné est calculée en additionnant les taux de fécondité par cohorte et période dans une colonne (une période) donnée du tableau 6 jusqu’à cet âge, et en multipliant par 5 (tableau 8). Par exemple, la fécondité cumulée jusqu’à l’âge de 30 ans au cours de la période 5-9 ans avant l’enquête est égale à 5.(0,068 + 0,250 + 0,291)=3,047.
Tableau 8 Fécondité cumulée par période (F), Malawi, EDS 2004
Groupe d’âge de la cohorte à la fin de chaque période avant l’enquête, | Période avant l’enquête (j) | ||||||
|---|---|---|---|---|---|---|---|
0-4 (j=0) | 5-9 (j=1) | 10-14 (j=2) | 15-19 (j=3) | 20-24 (j=4) | 25-29 (j=5) | 30-34 (j=6) | |
| 15-19 (k=1) | 0,298 | 0,342 | 0,398 | 0,403 | 0,455 | 0,413 | 0,416 |
20-24 (2) | 1,566 | 1,591 | 1,749 | 1,644 | 1,811 | 1,686 |
|
25-29 (3) | 2,935 | 3,045 | 3,375 | 3,202 | 3,317 |
|
|
30-34 (4) | 4,108 | 4,357 | 4,843 | 4,570 |
|
|
|
35-39 (5) | 5,129 | 5,345 | 6,115 |
|
|
|
|
40-44 (6) | 5,738 | 6,091 |
|
|
|
|
|
45-49 (7) | 6,051 | 6,406 |
|
|
|
|
|
On calcule deux estimations de l’indice synthétique de fécondité. La première est celle de la période 0-4 ans avant l’enquête ; elle est calculée directement à partir des données (6,1 enfants par femme). La fécondité de la période 5-9 ans avant l’enquête est obtenue en faisant 6,091 + 5.(0,063)=6,406 enfants par femme.
La date médiane des interviews de cette EDS étant en novembre 2004, on peut considérer que les deux estimations s’appliquent à mai 2002 et mai 1997 respectivement. Ces résultats suggèrent une baisse de l’indice synthétique de fécondité de 0,4 enfant par femme entre les deux périodes, mais un décalage et une omission des naissances les plus récentes peuvent donner une impression exagérée de baisse.
Etape 7 : Calculer les quotients P/F
Les quotients P/F sont calculés en divisant les cellules équivalentes dans les tableaux 7 et 8 (tableau 9).
Tableau 9 Quotients P/F, Malawi, EDS 2004
Groupe d’âge de la cohorte à la fin de chaque période avant l’enquête, | Période avant l’enquête (j) | ||||||
|---|---|---|---|---|---|---|---|
0-4 (j=0) | 5-9 (j=1) | 10-14 (j=2) | 15-19 (j=3) | 20-24 (j=4) | 25-29 (j=5) | 30-34 (j=6) | |
| 15-19 (k=1) | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 |
20-24 (2) | 1,028 | 1,035 | 1,003 | 1,032 | 0,977 | 1,002 |
|
25-29 (3) | 1,027 | 1,054 | 0,984 | 1,039 | 0,963 |
|
|
30-34 (4) | 1,067 | 1,063 | 0,990 | 0,998 |
|
|
|
35-39 (5) | 1,102 | 1,082 | 0,954 |
|
|
|
|
40-44 (6) | 1,114 | 1,080 |
|
|
|
|
|
45-49 (7) | 1,139 |
|
|
|
|
|
|
Les accroissements réguliers des quotients P/F au fil des âges au cours des deux périodes les plus récentes indiquent clairement qu’une baisse de la fécondité est en cours. Rien de semblable n’apparaît dans les quotients de la période 10-14 ans avant l’enquête. La baisse de la fécondité au Malawi doit donc avoir débuté environ dix ans avant l’enquête, vers 1994.
Les quotients P/F montrent qu’il y a eu des omissions et des décalages de naissances dans certaines cohortes et à certaines périodes. Par exemple, les données sur les naissances survenues 10-14 ans avant l’enquête donnent des quotients P/F inférieurs à l’unité. En outre, le quotient relatif aux naissances 10-14 ans avant l’enquête chez les femmes âgées de 20-24 ans (1,003) s’écarte clairement des quotients des femmes du même âge 5-9 ans et 15-19 ans avant l’enquête. Ce pourrait être la conséquence d’une hausse de la fécondité au cours de la période, mais cela semble peu vraisemblable. Plus probablement – puisque les quotients sont trop bas au cours de cette période – des naissances ont été décalées vers cette période (effets de Brass ou de Potter éventuels), gonflant donc les estimations de F et réduisant les quotients. Les femmes âgées de 45-49 ans semblent avoir omis certaines de leurs naissances dans toutes les périodes 5-25 ans avant l’enquête, les quotients P/F pour cette cohorte sont plus faibles que ceux de la cohorte des femmes âgées de 40-44 ans à l’enquête.
Autres lectures et références
Le calcul des quotients P/F à partir des données d’enquête a été exposé au début des années 1980 par Hobcraft et autres (Goldman and Hobcraft 1982 ; Hobcraft, Goldman and Chidambaram 1982). Hobcraft, Goldman and Chidambaram (1982), dans leur présentation de la méthode, analysent les taux de fécondité par cohorte et période par durée de mariage (et âge au mariage) et par durée depuis la première naissance (et âge à la première naissance).
Au-delà des sources déjà citées, la méthode a été utilisée dans un certain nombre d’analyses des données de l’Enquête mondiale de fécondité et des EDS. Il y a eu par exemple des applications au Lesotho (Timæus and Balasubramanian 1984), au Zimbabwe (Muhwava and Timæus 1996), en Afrique de l’ouest (Onuoha and Timæus 1995) et au Népal (Collumbien, Timæus and Acharya 2001). Hinde and Mturi (2000) ont appliqué la méthode aux données tanzaniennes en utilisant la durée de mariage.
Cleland J. 1996. "Demographic data collection in less developed countries", Population Studies 50(3):433-450. doi: https://dx.doi.org/10.1080/0032472031000149556
Collumbien M, IM Timæus and L Acharya. 2001. "Fertility decline in Nepal," in Sathar, ZA and JF Philips (eds). Fertility Transition in South Asia. Oxford: Oxford University Press, pp. 99-120.
Goldman N and J Hobcraft. 1982. Birth Histories. WFS Comparative Studies 17. Voorburg, Netherlands: International Statistical Institute.
Hinde A and AJ Mturi. 2000. "Recent trends in Tanzanian fertility", Population Studies 54(2):177-191. doi: https://dx.doi.org/10.1080/713779080
Hobcraft JN, N Goldman and VC Chidambaram. 1982. "Advances in the P/F ratio method for the analysis of birth histories", Population Studies 36(2):291-316. doi: https://dx.doi.org/10.2307/2174202
Muhwava W and IM Timæus. 1996. Fertility Decline in Zimbabwe. Centre for Population Studies Research Paper 96-1. London: London School of Hygiene & Tropical Medicine.
Onuoha NC and IM Timæus. 1995. "Has a fertility transition begun in West Africa?", Journal of International Development 7(1):93-116. doi: https://dx.doi.org/10.1002/jid.3380070107
Potter JE. 1977. "Problems in using birth-history analysis to estimate trends in fertility", Population Studies 31(2):335-364. doi: https://dx.doi.org/10.2307/2173921
Schoumaker B. 2010. "Reconstructing fertility trends in sub-Saharan Africa by combining multiple surveys affected by data quality problems " Paper presented at Population Association of America 2010 Annual Meeting. Dallas, TX, April 15-17, 2010.
Schoumaker B. 2011. "Omissions of births in DHS birth histories in sub-Saharan Africa: Measurement and determinants " Paper presented at Population Association of America 2011 Annual Meeting. Washington D.C., March 31 - April 2, 2011.
Timæus IM and K Balasubramanian. 1984. Evaluation of the Lesotho Fertility Survey 1977. WFS Scientific Reports, 58. Voorburg, Netherlands: International Statistical Institute.
- Printer-friendly version
- Log in to post comments
