Estimation directe de la mortalité des jeunes enfants à partir d’histoires génésiques

Contexte

Nous traitons ici de l’utilisation des données d’histoires génésiques complètes (en anglais : full birth histories, FBH) ou tronquées (en anglais : truncated birth histories, TBH) pour estimer la mortalité des jeunes enfants. La caractéristique essentielle de ces données est que pour chaque naissance incluse, la date de naissance, la survie et (en cas de décès) la date du décès sont enregistrés. L’analyse des données s’appuie sur la construction de tables de mortalité. L’estimation indirecte de la mortalité des jeunes enfants, et l’estimation de la mortalité des jeunes enfants à partir de la survie d’une naissance récente, sont traitées dans les chapitres sur l’estimation indirecte de la mortalité des jeunes enfants et la technique de la naissance précédente, respectivement.

Données nécessaires et hypothèses

Données nécessaires

Pour chaque femme d’âge fécond (dans certains contextes pour des raisons culturelles, la collecte d’information ne porte que sur les femmes déjà mariées) :

• le nom de chaque enfant né vivant ;
• le mois et l’année de naissance de chaque enfant ;
• le sexe de l’enfant (facultatif) ;
• si l’enfant est encore en vie ; et
• si l’enfant est décédé, son âge au décès (dans les EDS, l’âge au décès est recueilli en jours pour les décès dans les 28 premiers jours, en mois pour les décès entre un et 23 mois, et en années au-delà).

Hypothèses importantes

• Les enfants encore en vie et les enfants décédés sont déclarés avec la même précision.
• Les dates de naissance et de décès sont déclarées avec une précision raisonnable.
• Il n’y a pas de corrélation entre les risques de mortalité des enfants et les taux de survie des mères (que ce soit du fait de la mortalité ou de la migration) dans la population.

Précautions et mises en garde

Le travail sur des données collectées directement présente des dangers provenant de deux sources. Le premier est le risque de biais de survie, puisque seules les femmes vivantes sont interrogées sur leur histoire génésique détaillée à l’origine des données. Dans les situations où il se pourrait que les mères décédées aient eu une fécondité différente de celles des femmes survivantes, ou que leurs enfants aient fait face à des risques de décéder différents, il existe un risque de biais important dans les estimations obtenues. Divers aspects du biais de survie sont présentés dans l’introduction à l’analyse de la mortalité des jeunes enfants, dans la section traitant des effets du VIH sur l’estimation de la mortalité des jeunes enfants.

Le second danger provient du biais de troncature, si une limite d’âge supérieure s’applique aux femmes dont on recueille les histoires génésiques détaillées ; ce biais est d’autant plus significatif qu’on remonte plus loin dans le temps. Si on applique une limite d’âge de 49 ans lors de la collecte des données, l’information disponible pour la période 10 ans avant l’enquête ne porte que sur les femmes alors âgées de moins de 40 ans. La mortalité des jeunes enfants estimée à partir de telles données pour des périodes de plus en plus anciennes reposera progressivement sur les histoires génésiques de femmes de plus en plus jeunes. Il peut en résulter un biais de mesure, car cette troncature entraine une surreprésentation des premières naissances parmi les jeunes femmes ; la mortalité des jeunes enfants ainsi mesurée risque donc d’être d’autant plus surestimée que la période est ancienne. Certains résultats montrent que cette surestimation est contrebalancée par une sous-estimation due aux erreurs de mémoire (et à l’omission sélective des enfants qui sont décédés dans un passé lointain).

Evaluation de la qualité des données et analyse des données

Indépendamment de ce que l’on peut savoir sur le mode de collecte des données et sur la façon dont les enquêteurs ont été formés et supervisés, une appréciation méticuleuse de la qualité des données est une première étape essentielle de toute analyse. Toutes les séries de données contiennent des erreurs, qui peuvent provenir de nombreuses sources, telles que certains raccourcis pris par des interviewers ou un interviewé qui, simplement, ne connaît pas la réponse correcte à une question. Chaque section ci-dessous commence par une description des techniques d’évaluation de la qualité des données avant de passer aux méthodes d’analyse. Ces techniques d’évaluation examinent à la fois la cohérence interne d’une série de données et la cohérence externe par comparaison avec d’autres séries de données pour la même population. Notez en passant que la présence d’erreurs ne signifie pas nécessairement qu’une série de données ne doit pas être analysée, l’important est d’apprécier l’ampleur de ces erreurs et d’en tenir compte quand on interprète les résultats.

L’histoire génésique complète : évaluation de la qualité des données

La première étape d’une évaluation systématique de la qualité des données consiste à examiner la fréquence des valeurs manquantes. Dans une histoire génésique complète, des valeurs peuvent manquer pour diverses raisons. Par exemple, des ménages entiers inclus dans le plan de sondage original peuvent manquer. Il se peut en outre qu’au sein d’un ménage interviewé des femmes éligibles ne puissent pas être interrogées. Par ailleurs, des informations spécifiques peuvent manquer au sein d’une histoire génésique lorsque la femme interrogée ne connaît pas la date de naissance d’un enfant, ou qu’elle ignore si un enfant est encore en vie, ou (en cas de décès) l’âge au décès. Les proportions d’événements susceptibles d’être affectés par ces erreurs doivent être examinées. Les items manquants peuvent être imputés au cours du nettoyage des données, mais les valeurs imputées doivent être signalées. L’absence de valeurs manquantes ne doit pas être considérée comme un marqueur fort de la qualité des données ; cela peut même être considéré comme un avertissement : dans certaines enquêtes, les enquêteurs et les superviseurs sont formés pour éviter les valeurs manquantes et, dans ces cas, les données peuvent être plus ou moins fabriquées par l’interviewer.

La seconde étape dans l’évaluation de la qualité des données consiste à rechercher des irrégularités peu vraisemblables dans les résultats agrégés. Les irrégularités le plus souvent détectées concernent les rapports de masculinité à la naissance, dans les distributions annuelles de naissances vivantes, et les âges au décès. En l’absence d’intervention, les rapports de masculinité dans les populations humaines sont généralement compris entre 100 et 106 garçons pour 100 filles. Des rapports de masculinité à la naissance hors de cet intervalle indiquent probablement une erreur. Des rapports de masculinité qui augmentent quand on remonte vers des cohortes nées longtemps avant l’enquête sont des indicateurs particulièrement clairs d’une erreur, dans ce cas une sous-déclaration des naissances féminines anciennes.

En l’absence d’événements majeurs, les naissances évoluent normalement de manière régulière au fil des années, les variations saisonnières n’affectant pas les nombres annuels. D’éventuelles erreurs peuvent être détectées par le calcul de ‘rapports de naissances’, définis comme

$$\frac{2B_t}{B_{t-1}+B_{t+1}}$$

où B_t est le nombre de naissances déclarées l’année t. Une erreur courante dans les fichiers de données des EDS a été intitulée “transfert de naissances”. Les enquêtes EDS recueillent de nombreuses données supplémentaires sur les enfants nés depuis une date précise, en général le 1^er janvier de l’année cinq ans avant l’enquête. Il arrive souvent que les naissances survenues cette année soient déclarées comme ayant eu lieu l’année précédente, sans doute pour réduire la charge de travail. Il en résulte un déficit des naissances l’année qui suit la date marquant le début de la période concernée, et un surplus l’année qui précède. Les rapports de naissances feront apparaitre cette erreur, puisque le rapport sera bas pour l’année qui débute à la date de référence et sera élevé pour l’année qui précède. Ce transfert de naissances est très souvent plus marqué pour les enfants décédés que pour ceux encore en vie, aussi est-il bon de calculer des rapports séparés pour les enfants survivants et décédés.

Des irrégularités dans la déclaration des âges au décès peuvent être détectées de la même façon par le calcul du rapport entre les décès à l’âge x et la moyenne des décès aux âges encadrants (x – 1) et (x + 1). Dans les données des EDS, il y a généralement un excès de décès à 7 jours, dans une moindre mesure à 14 jours, et à 12 mois.

Les EDS publient ces indicateurs de qualité des données au niveau agrégé (national) dans les rapports d’enquêtes (souvent en Annexe C). Ceux qui veulent réaliser des analyses à un niveau plus fin doivent calculer ces indicateurs par eux-mêmes.

Les indicateurs ci-dessus sont des mesures de vraisemblance interne. Mais des données peuvent être vraisemblables en interne et pourtant erronées. Les données doivent être aussi évaluées par comparaison avec d’autres enquêtes pour la même population. Les comparaisons par cohorte sont particulièrement utiles, par exemple la comparaison du nombre moyen d’enfants nés vivants des femmes âgées de 30-34 ans dans une enquête au nombre moyen d’enfants nés vivants des femmes âgés de 35-39 ans dans une autre enquête menée cinq ans plus tard. Les mêmes comparaisons peuvent être faites avec les nombres moyens d’enfants décédés. Des suites de naissances par année civile peuvent aussi être comparées pour des périodes qui se chevauchent, mais en ayant à l’esprit que les naissances du passé sont tronquées de façon croissante quand les histoires génésiques ne sont obtenues qu’auprès des femmes âgées de 15-49 ans au moment de l’enquête.

L’histoire génésique complète des naissances : calcul des indicateurs de mortalité des jeunes enfants dans les cohortes de naissance

Les indicateurs de mortalité des jeunes enfants couramment utilisés sont exprimés comme des probabilités. Ainsi, le taux de mortalité infantile est la probabilité de décéder avant le premier anniversaire, ₁q₀ (ceci est une approximation car le taux de mortalité infantile est conventionnellement défini comme le rapport du nombre de décès infantiles au cours d’une année au nombre de naissances de cette même année, une valeur très voisine de ₁q₀). Le taux de mortalité avant 5 ans est la probabilité de décéder avant le 5^ème anniversaire, ₅q₀. Au sens strict, les probabilités sont des mesures relatives à des cohortes réelles, même si la plupart des tables de mortalité calculent des mesures relatives à des cohortes synthétiques, pour des périodes, à partir de taux de mortalité par âge et période. Il est très simple de calculer des probabilités pour des cohortes à partir d’histoires génésiques complètes. Par exemple, le taux de mortalité infantile par cohorte pour les enfants nés 12 à 23 mois avant l’enquête est simplement le nombre de ces enfants décédés avant l’âge d’un an divisé par le nombre de naissances. De même, le taux de mortalité avant 5 ans par cohorte pour les enfants nés 5 à 9 ans avant l’enquête est le nombre d’enfants décédés avant leur 5^ème anniversaire divisé par le nombre de naissances il y a 5-9 ans. A la figure 1, on a représenté sur un diagramme de Lexis la probabilité par âge et cohorte de décéder avant le 1^er anniversaire pour la cohorte née en juillet 2001 (en vert), et la mortalité par âge et période des enfants âgés de 5 mois au cours de l’année 2002 (le rectangle bleu, reprenant un exemple qui sera utilisé plus loin dans ce chapitre).

Image

Figure 1: Lexis diagram representation of age-cohort mortality by age 1 (green) and age-period mortality for 5-month olds (blue)

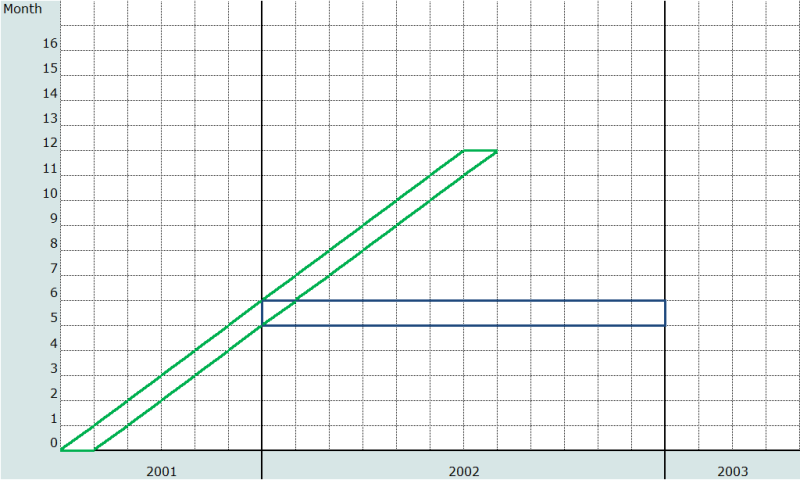
 Le tableau 1 présente les données pour le calcul de la probabilité par âge et cohorte de décéder avant l’âge d’un an pour les enfants nés 12-23 mois avant l’enquête et de la probabilité de décéder avant 5 ans pour la cohorte née 5 à 9 ans avant l’enquête, d’après l’EDS 2004 du Malawi.

Tableau 1 Calcul du taux de mortalité infantile et du taux de mortalité avant 5 ans, Malawi, EDS 2004

Notez qu’il n’y a pas d’interprétation par période (en transversal) de ces valeurs de cohortes ; dans l’exemple du taux de mortalité avant 5 ans, la probabilité par cohorte reflète des risques de mortalité dans chacune des 10 années précédant l’enquête. Notez aussi que la probabilité de décéder avant l’âge x ne peut être calculée que pour des cohortes nées au moins x années avant l’enquête. Ces deux considérations limitent la valeur des mesures de cohorte, car dans la plupart des cas les analystes et les responsables politiques sont davantage intéressés par les mesures transversales.

L’histoire génésique complète : calcul des indicateurs de mortalité des jeunes enfants par période

Les mesures par période sont estimées en utilisant le concept de cohorte synthétique. Les taux de mortalité pour des intervalles d’âge restreints et des périodes définies sont calculés sur la base d’événements et d’exposition au risque dans des rectangles du diagramme de Lexis. Les taux sont ensuite convertis en probabilités, en utilisant les relations démographiques classiques (voir, par exemple, Preston, Heuveline et Guillot (2001)) et en faisant généralement quelques hypothèses peu contraignantes sur la distribution des décès dans chaque rectangle. Enfin, les probabilités de décéder sont appliquées successivement à une cohorte hypothétique de naissances ; il en résulte une courbe de survie ℓ(x) pour chaque âge x, à partir de laquelle on tire facilement des probabilités de décéder.

Les données des histoires génésiques complètes de naissances se prêtent aisément à ces calculs de tables de mortalité. Si les données sont collectées selon la pratique des EDS – en mois et année pour les dates de naissance ; en jours, mois ou années (en fonction de l’âge) pour les âges au décès– les décès peuvent être situés sans grande ambiguïté dans des rectangles âge-période du diagramme de Lexis (il restera une légère ambiguïté, du fait de l’imprécision de l’information sur la date de naissance et l’âge au décès, mais l’impact dépendra de la taille des rectangles.) Nous décrivons ici une démarche fondée sur le calcul de taux de mortalité par âge pour une seule année civile (taux par âge et période) pour la mortalité avant 5 ans. Il est facile d’étendre ensuite à d’autres périodes de temps. On suppose que les données sont reprises dans un format EDS classique, c’est-à-dire que les dates de naissance sont enregistrées en nombre de mois depuis le 1^er janvier 1900, et les âges au décès sont en jours, mois ou années. On doit disposer de données individuelles. L’unité d’âge est le mois. Les calculs de base sont donc des taux de mortalité par âge, par mois d’âge et année civile. Ces taux sont convertis en probabilités de décéder chaque mois. Ces probabilités sont ensuite converties en probabilité de survie, et sont combinées sur tout intervalle d’âge nécessaire (en particulier, jusqu’à 5 ans). L’essentiel du calcul consiste à assigner les décès et les expositions au risque à des segments d’âge d’un mois au cours d’une année civile.

Traitement des données

Dans une série de données sur les naissances de type EDS, on utilise quatre variables :

1. b3, date de naissance en nombre de mois depuis le 1^er janvier 1900 ;
2. b5, survie de l’enfant;
3. b6, âge au décès, où le premier chiffre indique l’unité (1, jours ; 2, mois ; et 3, années) et les deuxième et troisième chiffres la valeur dans cette unité ; et
4. v005, coefficient de pondération d’échantillonnage, en millions.

Notez que la variable b7, âge au décès (en mois, par imputation), n’est pas utilisée. Cette variable ne se prête pas à la procédure de calcul des taux de mortalité décrite ici car, dans les cas ou l’âge au décès est enregistré en années, le mois ‘imputé’ est en fait égal à la limite inférieure de l’intervalle (c’est-à-dire que si l’âge au décès est enregistré comme ‘3 ans’, l’âge imputé en mois est 36 mois). Cette variable conduirait donc à une localisation systématiquement erronée des décès dans le temps.

Application de la méthode

Etape 1: Traitement de l’âge au décès et calcul de la date de naissance et de l’âge au décès estimés

Nous voulons situer les décès par mois de leur survenue. Comme nous n’avons pas une date de naissance précise (car elle est exprimée seulement en nombre de mois depuis le 1^er janvier 1900), et qu’en général nous n’avons par un âge au décès précis (sauf pour les décès néonataux), il nous faut imputer à la fois la date de naissance et l’âge au décès. Nous pouvons le faire en utilisant des nombres aléatoires.

Il n’est évidemment pas souhaitable – entre autres par manque de reproductibilité – d’utiliser pour cela un vrai générateur de nombres au hasard. En outre, une ‘vraie’ randomisation risque de produire une fausse impression de précision. A la place, nous proposons de créer des nombres pseudo-aléatoires à partir de variables couramment disponibles dans les données des EDS et qui peuvent être appliquées dans l’algorithme ci-dessus. Il est facile de créer de nouvelles variables en répartissant les enregistrements en déciles sur la base du jour d’interview (v016 dans une EDS) et du numéro de ménage (v002). (Ces variables ont été choisies parce qu’il est peu vraisemblable qu’elles soient corrélées avec la mortalité des jeunes enfants). Ces nouvelles variables prendront des valeurs dans l’intervalle (0, 1 … 9). En divisant ces valeurs par 10 et en ajoutant 0,05 on obtient deux nouvelles variables distribuées uniformément, aléa1 et aléa2, qui prennent des valeurs dans l’intervalle (0,05, 0,15, …, 0,95).

Il est ensuite facile d’imputer une date de naissance (ddn, en mois), si les naissances du mois de l’interview sont exclues de l’analyse, en ajoutant aléa1 à b3 (la date de naissance en nombre de mois depuis le 1^er janvier 1900). La méthode d’imputation de l’âge au décès (en unités mensuelles) dépend de l’’unité’. Quand ‘unité’ = 1 (c’est-à-dire que l’âge au décès est mesuré en jours), l’âge au décès (aad) peut être estimé comme (‘valeur’+ aléa2)/31 (quand l’âge au décès est en jours, ce n’est pas nécessaire, mais nous le présentons ici pour être systématique) ; quand ‘unité’ = 2, l’âge au décès est ‘valeur’ + aléa2, et quand ‘unité’ = 3, l’âge au décès est (‘valeur’ + aléa2)*12.

Etape 2: Situer les décès au cours de l’année étudiée

Pour chaque taux de mortalité par mois d’âge, les événements sont les décès à cet âge au cours de la période étudiée. L’étape 1 a imputé l’âge au décès en mois. La date de décès ddd est égale à la somme du mois de naissance imputé ddn et de l’âge au décès imputé aad. Si l’âge au décès imputé appartient à l’intervalle d’âge et si la date de décès imputée tombe dans la période étudiée, l’événement est retenu.

Etape 3: Calcul de l’exposition au risque

Le calcul de l’exposition au risque est subtil, mais relativement direct. L’intervalle d’âge se réfère aux âges (définis dans les unités appropriées) pour lesquels nous voulons mesurer la mortalité. Nous désignons la limite basse de l’intervalle d’âge comme x_l et la limite haute comme x_h.

La période étudiée est la mesure de l’intervalle de temps pour laquelle nous cherchons à estimer la mortalité ; elle est définie comme la période (t₂ – t₁), où t₂ est la date de fin de la période étudiée et t₁ la date de début, mesurées dans les mêmes unités que celle définie par l’intervalle d’âge.

Graphiquement nous cherchons ensuite à mesurer la mortalité à l’âge et dans la période définis par les lignes épaisses sur la figure 2.

Image

Figure 2: Lexis diagram showing calculation of exposure to risk

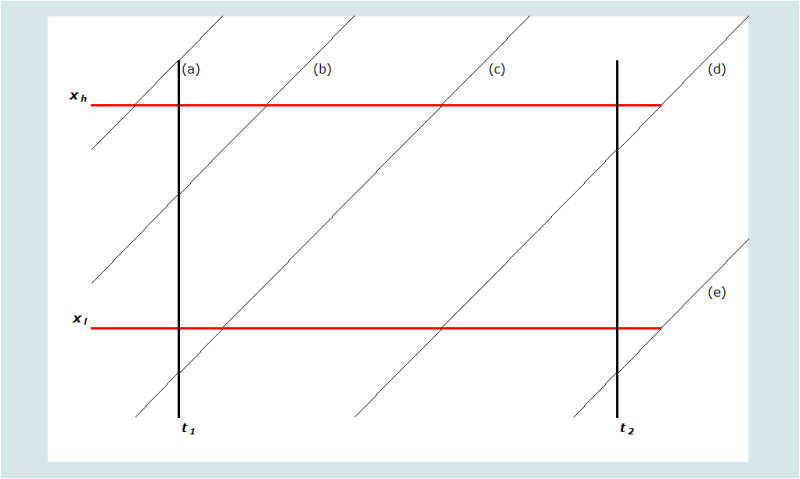
La trajectoire d’un individu par âge et période s’inscrit sur une diagonale (comme dans un diagramme de Lexis classique). Cinq scénarios possibles sont représentés, étiquetés de (a) à (e). La position d’un individu dans l’espace peut être définie par son âge à t₁, x_t1. Il s’ensuit que toute personne âgée de x à t₁, si elle ne décède pas avant t₂, doit être âgée de x_t2 = x_t1+(t₂ – t₁) à t₂. Nous définissons l’âge au décès des personnes décédées dans un intervalle d’âge donné au cours de la période étudiée comme x_d. La contribution relative de chaque scenario à l’exposition au risque est déterminée par l’algorithme du tableau 2.

Tableau 2 Algorithme pour déterminer l’exposition au risque

En appliquant ces règles à chaque individu pour définir l’exposition au risque dans l’intervalle d’âge au cours de la période étudiée et en agrégeant, on obtient l’exposition totale au risque, qui est le dénominateur du taux de mortalité. La somme des décès survenus dans l’intervalle d’âge au cours de la période étudiée fournit le numérateur.

Etape 4: Pondération et cumul des événements et de l’exposition au risque

La variable de pondération dans un fichier EDS standard est v005. Elle a une moyenne de 1 000 000. Pour éviter de donner l’impression que l’échantillon est énorme (et que les intervalles de confiance sont très étroits), nous recommandons d’abord de recalculer les pondérations et de définir une nouvelle variable wgt = v005/1 000 000. Les taux de mortalité peuvent être calculés en tenant compte des contributions de chacun des N enfants dans l’enquête au nombre des événements et au temps total d’exposition. Le taux de mortalité par âge aux âges x à x + 1 (en mois) au cours d’une période j est

$$M\left(x,j\right)=\frac{{\displaystyle \sum _{i=1}^{N}D\left(i,x,j\right).wgt\left(i\right)}}{{\displaystyle \sum _{i=1}^{N}E\left(i,x,j\right).wgt\left(i\right)}}$$

où D(i,x,j) est une variable binaire indiquant le décès de l’enfant i à l’âge x l’année j (1 si le décès survient, sinon 0), E(i,x,j) est le temps d’exposition de l’enfant i à l’âge x l’année j, et où wgt(i) est la pondération d’échantillonnage (moyenne 1,0) de l’enfant i.

Etape 5: Calcul des probabilités de décéder à partir des taux de mortalité par âge

Les taux calculés à l’étape 4 sont par mois d’âge d’exposition. Il est donc nécessaire d’en tenir compte en adaptant la formule classique de passage d’un taux à une probabilité de décéder par période. Comme nous avons fait diverses hypothèses simplificatrices et que nous travaillons avec des intervalles d’âge étroits, il convient de supposer que les décès sont distribués régulièrement entre chaque intervalle d’âge mensuel. Nous pouvons donc calculer q(x) comme

$$q\left(x,j\right)=\frac{\frac{M\left(x,j\right)}{12}}{\left(1+\frac{M\left(x,j\right)}{24}\right)}$$

Les probabilités de survie de la naissance jusqu’à n’importe quel âge peuvent être obtenues en combinant les probabilités de survie mensuelles (c’est-à-dire (1 - q(x,j))). Ainsi par exemple

$${}_{5}q{}_{{}_0}^j=1-{\displaystyle \prod _{x=0}^{59}\left(1-q\left(x,j\right)\right)}$$

Exemple

Comme on l’a dit, l’estimation directe de la mortalité des jeunes enfants à partir des historiques de naissances s’appuie sur l’utilisation des enregistrements individuels plutôt que sur des tableaux de données agrégées. C’est pourquoi l’exemple que nous prenons illustre la méthode à partir d’un nombre restreint d’enregistrements tirés d’une EDS, plus précisément la mortalité des enfants âgés de 5 mois en 2002 d’après l’EDS 2004 du Malawi. Seuls les enfants nés entre le 1^er juillet 2001 et le 31 juillet 2002 sont exposés au risque de décéder à l’âge de 5 mois au cours de l’année 2002 (les enfants nés avant le 1^er juillet 2002 seraient âgés de 6 mois ou plus au début de l’année 2002, et ceux nés après le 31 juillet 2002 n’auraient pas atteint l’âge de 5 mois au cours de l’année). Nous n’avons fait figurer que les enregistrements pertinents, c’est-à-dire ceux correspondant à des naissances entre les mois 1218 et 1230 (en nombres de mois depuis le 1^er janvier 1900, soit de juillet 2001 à juillet 2002). Dans la pratique, nous exclurions aussi les naissances ayant donné lieu à un décès avant cinq mois d’âge, mais nous les garderons dans l’exemple pour montrer que nous les excluons des calculs.

Le tableau 3 présente les variables essentielles pour 50 enregistrements tirés de l’EDS 2004 du Malawi. Ce sont des enregistrements de naissances, pas de femmes.

Tableau 3 Données de base d’histoires génésiques pour l’estimation directe de la mortalité des jeunes enfants

Etape 1: Traitement de l’âge au décès et calcul de la date de naissance et de l’âge au décès estimés

Les nombres aléatoires aléa1 et aléa2 sont établis comme il a été expliqué plus haut. Il en résulte les valeurs révisées des dates de naissance et âge au décès, ddn’ et aad’. La date de décès ddd’ est estimée comme la somme du mois de naissance imputé ddn’ et du mois de décès imputé aad’. Les ddd’ figurent à la colonne 10 du tableau 4.

Tableau 4 Calcul de la date de naissance, de l’âge au décès et de la date de décès imputés. Malawi, EDS 2004 (50 observations)

Etape 2: Situer les décès au cours de l’année étudiée

Nous retenons les décès survenus entre les mois 1224 et 1235 (dans une numérotation depuis janvier 1900). Les décès correspondant aux enregistrements 3, 6, 31 et 41 au tableau 4 sont donc exclus car ils ne se sont pas produits en 2002. Les décès des enregistrements 11 et 45 ne sont pas pris en compte ici car les enfants sont décédés respectivement à l’âge de 2 mois et 1 mois et ne sont donc pas exposés au risque de décéder à 5 mois.

Etape 3: Calcul de l’exposition au risque

Le tableau 5 présente le calcul de l’exposition au risque pour les 50 cas retenus. La règle de détermination de l’exposition figure dans la colonne ‘Scenario’. L’exposition qui en résulte figure aux deux colonnes suivantes pour ceux qui survivent au-terme de la période étudiée et pour ceux qui décèdent au cours de la période.

Pour les enfants qui survivent à l’âge de 6 mois, ceux nés les mois 1219 à 1229 comptent pour un mois entier d’exposition au cours de l’âge-période considéré (c’est-à-dire de 5 mois à 6 mois exacts). Ainsi l’enregistrement 1 (né en 1223,55) contribue pour un mois entier. Un enfant né le mois 1218 contribuera pour (ddn – 1218) mois et donc l’enregistrement 23 (né en 1218,85) contribue pour 0,85 mois. Un enfant né le mois 1230 contribuera pour (1231 – ddn) mois et donc l’enregistrement 7 contribue pour 1231 – 1230,55 = 0,45 mois. Les enfants nés les mois 1219 à 1229 qui décèdent à 5 mois d’âge contribueront pour (aad – 5) mois d’exposition ; ainsi le décès dans l’enregistrement 14 survient à 5,25 mois et contribue pour 0,25 mois d’exposition.

Tableau 5 Calcul de l’exposition au risque pour l’estimation de la mortalité des jeunes enfants. Malawi, EDS 2004 (50 observations)

Etape 4: Pondération et cumul des événements et de l’exposition au risque

L’étape finale avant le calcul du taux de mortalité consiste à tenir compte de la pondération d’échantillonnage de chaque enregistrement à la fois pour les décès et pour le temps d’exposition, puis à faire la somme des décès et des expositions. Les colonnes 6 et 7 du tableau 5 présentent l’exposition au risque des survivant et des décédés. Les colonnes 8 et 9 résultent de la multiplication des colonnes 6 et 7 respectivement par la pondération d’échantillonnage v005/ 1 000 000. Le taux de mortalité par âge M(5,2002) est ensuite calculé en divisant la somme des décès pondérés par la somme des temps d’exposition pondérés :

$M(x,j)=\frac{{\displaystyle \sum _{i=1}^{N}D(i,x,j)\times wgt(i)}}{{\displaystyle \sum _{i=1}^{N}E(i,x,j)\times wgt(i)}}=\frac{\mathrm{6,389}}{\mathrm{59,317}}=\mathrm{0,1077}.$

Etape 5: Calcul des probabilités de décéder à partir des taux de mortalité par âge

Les taux calculés à l’étape 4 sont par mois d’exposition. Il est donc nécessaire d’en tenir compte en adaptant la formule classique de passage d’un taux à une probabilité de décéder par période. Comme nous avons fait diverses hypothèses simplificatrices et que nous travaillons avec des intervalles d’âge étroits, il convient de supposer que les décès sont distribués régulièrement entre chaque intervalle d’âge mensuel, même pour le premier mois de vie. Nous pouvons donc calculer q(x) comme

$$q(5,2002)=\frac{\frac{M(5,2002)}{12}}{(1+\frac{M(5,2002)}{24})}=\frac{\frac{0,1077}{12}}{(1+\frac{0,1077}{24})}=\frac{0,008975}{1+0,004488}=0,008935.$$

Une fois tous les q(x,j) calculés, ils peuvent être transformés en leurs compléments, les probabilités de survie qui, combinées entre elles, donnent les probabilités de survivre et de décéder jusqu’aux différents âges.

Pour obtenir des taux et des probabilités couvrant des périodes de plusieurs années, les sommes pondérées obtenues à l’étape 4 le sont sur toutes ces années. L’étape 5 reste la même.

Notez que la procédure décrite ici diffère de celle utilisée par les EDS, qui consiste à calculer les probabilités directement pour des quasi-cohortes (Croft et al. 2023). Les calculs sont faits dans huit groupes d’âge : néonatal, 1-2 mois, 3-5 mois, 6-11 mois et année par année de 1 à 4 ans. Pour chaque intervalle d’âge, les décès de la période sont déterminés à partir de la date de naissance et de l’âge au décès. Le nombre d’enfants exposés au risque est obtenu par approximation du nombre d’enfants qui entrent dans un intervalle d’âge au cours de la période. Cette approximation est la somme de tous les enfants qui entrent dans l’intervalle d’âge et qui en sortent (ou qui le feraient s’ils survivaient) au cours de la période, plus la moitié de ceux qui entrent dans l’intervalle d’âge au cours de la période mais qui en sortiraient après la période, plus la moitié de ceux qui sont entrés dans l’intervalle d’âge avant le début de la période mais qui en sortiraient au cours de la période.

Quelle que soit la procédure utilisée, il est nécessaire de disposer de données individuelles tirées des histoires génésiques complètes. Les calculs peuvent être réalisés à l’aide de tableaux détaillés, mais ce serait très fastidieux. Nous recommandons fortement le recours à des outils informatiques adaptés.

Interprétation

Quand on interprète les résultats, on doit avoir présent à l’esprit le risque de biais de sélection des répondantes, dû au fait que l’information est fournie par les femmes survivantes au sein des ménages enquêtés. En particulier, la mortalité des enfants nés dans un groupe auquel leurs mères n’appartiennent plus au moment de l’enquête n’est pas incluse dans les mesures. Si ces enfants ont une mortalité plus élevée que ceux nés de mères qui appartiennent encore au groupe, la mortalité sera sous-estimée. Le biais le plus important est sans doute celui qui résulte d’une prévalence élevée du VIH dans le groupe, car une telle prévalence, en l’absence d’un recours massif à la thérapie antirétrovirale, entraine une forte corrélation positive entre la survie de l’enfant et la survie de la mère (voir la section relative aux effets du VIH/Sida sur l’estimation de la mortalité des jeunes enfants). Mais dans toute population, il est fort probable qu’il y ait une certaine corrélation positive entre la survie de la mère et celle de l’enfant. Il peut y avoir d’autres sources de biais. Par exemple, quand l’immigration est importante, des femmes déclarent des enfants nés et élevés ailleurs, alors qu’une émigration importante élimine des réponses relatives à des enfants nés et élevés dans le groupe. Il est impossible de savoir a priori le sens et l’ampleur de tels biais, mais l’analyste doit avoir leur éventuel effet présent à l’esprit. Les non-réponses peuvent aussi être un problème si des femmes absentes durablement ne peuvent pas être interviewées personnellement, et si cette absence a une influence sur la mortalité de leurs enfants ou si cette absence est en partie due aux risques différents subis par leurs enfants.

Extension de la méthode : histoires génésiques tronquées

L’histoire génésique tronquée : Evaluation de la qualité des données

L’histoire génésique tronquée offre moins de possibilités de contrôles de qualité des données que l’histoire génésique complète, du fait même que la série d’événements déclarés est tronquée. Si la troncature porte sur la période, les événements déclarés doivent être représentatifs de la période couverte, alors que si la troncature porte sur le nombre d’événements, les événements déclarés peuvent être représentatifs seulement de l’ensemble des événements sur une courte période antérieure à l’enquête, et ceci va compliquer toute évaluation de la qualité de la suite des événements au fil du temps.

Comme pour l’histoire génésique complète, la première étape doit être un examen des données en valeur manquante. La deuxième étape doit impliquer l’examen des rapports de masculinité à la naissance et de l’attraction de certains âges au décès.

Il n’est pas possible d’envisager directement l’existence de transfert des naissances, puisqu’on ne dispose pas d’information détaillée sur les dates de naissance antérieures au point de troncature. Mais une évaluation indirecte est possible. Une histoire génésique tronquée devrait toujours commencer par le recueil d’une histoire génésique résumée. Les naissances et les décès de jeunes enfants pour les femmes d’un groupe d’âge à l’enquête peuvent donc être calculés à la fois à la date de l’enquête (à partir de l’histoire génésique résumée) et (avec une approximation pour les décès) à la date de troncature, en retranchant les naissances et les décès déclarés dans l’histoire génésique tronquée. Le calcul est précis pour les naissances, mais il est approximatif pour les décès de jeunes enfants car certains de ceux qui ont été déclarés dans l’histoire résumée se seront produits dans la période d’après troncature tout en concernant des enfants nés avant celle-ci ; mais le nombre de ces décès sera généralement faible, du fait que les risques de mortalité diminuent rapidement à mesure que les enfants avancent en âge. L’évaluation de la qualité des données s’appuie donc sur la comparaison entre la proportion d’enfants décédés (par groupe d’âge de la mère au moment de l’enquête) parmi les enfants nés après la date de troncature et celle parmi les enfants nés avant cette date.

La première proportion (enfants nés après la date) sera généralement inférieure à la seconde pour deux raisons. Tout d’abord, les enfants auront été exposés moins longtemps au risque de décéder. Ensuite, si la mortalité diminue au fil des années, ils auront aussi été exposés à des risques moindres aux différents âges. Mais si les enfants décédés sont systématiquement omis de la période post-troncature, ou s’ils sont déclarés dans l’histoire génésique résumée mais pas déclarés comme étant nés au cours de la période, le ratio des deux sera surestimé du fait des erreurs dans les données. Nous pouvons estimer un ratio vraisemblable en l’absence d’erreur à partir d’une histoire génésiques complète pour la même population à une date antérieure ou postérieure. Le tableau 6 présente des données pour la Mongolie, tirées de trois enquêtes sur la santé reproductive, une en 1998 qui incluait une histoire génésique complète et deux – en 2003 et 2008 – qui n’ont recueilli que des histoires tronqués. Les données de l’histoire génésique complète en 1998 sont utilisées pour calculer les proportions d’enfants décédés avant et après une date de troncature définie comme dans les enquêtes ultérieures ; les résultats sont ensuite comparés aux proportions calculées à partir des histoires tronquées en 2003 et 2008. Comme on peut le voir, les ratios tirés des histoires tronquées sont largement supérieurs à ceux tirés des histoires complètes, ce qui démontre clairement l’existence d’un transfert des enfants décédés hors de la période post-troncature. En l’absence d’une référence propre au pays , comme celle que fournit l’enquête de 1998 pour la Mongolie, on doit tenir des ratios de 3 ou plus comme preuve d’une omission probable d’enfants décédés au cours de la période de référence récente.

Tableau 6 Proportions d’enfants décédés selon que la naissance s’est produite avant ou après la date de troncature, Mongolie, Enquêtes sur la santé reproductive 1998, 2003 et 2008

L’histoire génésique tronquée : Calcul des indicateurs de mortalité des jeunes enfants par cohorte

Le calcul des probabilités de décès par cohorte à partir d’histoires génésiques tronquées suit le même principe que celui observé avec des histoires génésiques complètes : la probabilité de décéder avant l’âge x est égale au rapport entre le nombre d’enfants décédés et le nombre d’enfants nés vivants dans une cohorte née au moins x années avant l’enquête. Il y a toutefois une différence importante, clairement mise en évidence sur le diagramme de Lexis de la figure 1 : la valeur de x est contrainte par la date de troncature. Par exemple, si la date de troncature se situe 5 ans avant l’enquête, aucune cohorte de naissance n’aura été pleinement exposée au risque complet de décéder avant l’âge de 5 ans, et les cohortes pleinement exposées au risque jusqu’à l’âge de 2 ans seront constituées des naissances survenues 2, 3 et 4 ans avant l’enquête. Il y a donc des limites aux âges pour lesquels des indicateurs de mortalité peuvent être calculés.

L’histoire génésique tronquée : Calcul des indicateurs de mortalité des jeunes enfants par période

Fondamentalement, le calcul des indicateurs classiques à partir d’histoires génésiques tronquées suit les mêmes principes que lorsqu’on utilise des histoires génésiques complètes : calculer des taux par âge pour une période donnée, les convertir en estimations des probabilités de décéder dans des intervalles d’âge successifs, et appliquer les probabilités à une cohorte synthétique de naissance pour créer une table de mortalité. Le problème dans ce type d’analyse des histoires tronquées est le même que celui rencontré lors du calcul des indicateurs de cohortes, puisque le nombre de cas et le temps d’exposition au risque se réduisent progressivement à mesure que l’âge augmente. Ainsi, si le point de troncature se situe cinq ans avant l’enquête, les mesures aux âges de 3 et 4 ans s’appuieront sur de petits nombres et elles seront entourées d’une large marge d’erreur.

Références

Croft, Trevor N., Allen, Courtney K., Zachary, Blake W., et al. 2023. Guide to DHS Statistics. Rockville, Maryland, USA: ICF. https://www.dhsprogram.com/Data/Guide-to-DHS-Statistics/index.cfm

Preston SH, P Heuveline and M Guillot. 2001. Demography: Measuring and Modelling Population Processes. Oxford: Blackwell.