Probabilités d’agrandissement des familles
Introduction
Quand les femmes ou les parents pensent à « avoir des enfants », il s’agit généralement de commencer à former une famille ou d’avoir un autre enfant. La présente section traite des aspects séquentiels de la constitution de la descendance, en s’attachant aux proportions de mères ayant atteint une parité ou un rang de naissance donné et à la proportion de celles qui accroissent ensuite leur parité d’au moins un enfant supplémentaire.
L’information sur le rang de naissance s’obtient aisément à partir de deux questions simples du recensement : L’une sur la descendance atteinte par les femmes et l’autre sur les naissances au cours de l’année écoulée. Grâce à la première question, on peut décomposer les naissances de l’année passée par rang de naissance. On obtient de cette manière des informations supplémentaires sur les tendances de la fécondité et on peut évaluer les changements de la distribution de la descendance par parité en calculant les probabilités d’agrandissement des familles.
Une probabilité d’agrandissement des familles désigne la proportion de femmes qui passent d’une parité à la suivante. Les probabilités peuvent être calculées pour des cohortes de femmes définies par l’âge ou le mariage. On considère généralement des cohortes d’âge, les probabilités d’agrandissement étant dans ce cas calculées à partir de la distribution par parité des femmes d’un groupe d’âge donné. Pour les cohortes ayant achevé leur vie féconde, ces mesures restent fixes, sous condition que les femmes âgées ne soient pas soumises à une mortalité différentielle par parité. Mais pour les cohortes encore dans leur période féconde, les mesures changent du fait que des femmes passent à une parité plus élevée. Les mesures relatives aux jeunes femmes souffrent donc à la fois d’effets de censure et de sélection, les femmes ayant eu des enfants rapidement étant surreprésentées dans les combinaisons âge-parité avant la fin de la période féconde. Les comparaisons de probabilités d’agrandissement entre femmes jeunes et âgées sont donc trompeuses.
Brass (1985) décrit une technique pour projeter les probabilités d’agrandissement jusqu’à la fin de la période reproductive, afin que les données de parité des jeunes femmes puissent être utilisées. L’intérêt de décomposer la fécondité par parité est que différentes probabilités d’agrandissement peuvent répondre à différents facteurs, de sorte que l’évolution de certaines probabilités d’agrandissement peut nous renseigner sur les processus en œuvre dans les variations de la fécondité d’une population. Par exemple, les probabilités d’agrandissement mesurent aisément les restrictions de fécondité (ou leur absence) liées au nombre d’enfants déjà nés. Elles peuvent aussi être moins sujettes que d’autres indicateurs plus courants à certains types d’erreur sur les données (par exemple les erreurs sur la période de référence). Le calcul de taux de fécondité de premier rang, réalisé lors de la construction de probabilités d’agrandissement projetées, peut à la fois donner des indications sur la qualité des données et sur l’évolution de la fécondité.
Le calcul des probabilités d’agrandissement est simple pour les cohortes qui ont terminé leur vie féconde. La comparaison de cohortes successives peut donner des informations sur les tendances de la fécondité, mais des conclusions plus fiables peuvent être tirées s’il est possible de comparer les probabilités d’agrandissement des mêmes cohortes à travers plusieurs recensements. Pour les jeunes femmes, qui fournissent des informations sur des tendances plus récentes de la fécondité, une procédure plus élaborée est nécessaire. Il s’agit de prévoir la distribution par parité que les jeunes femmes auraient si elles conservaient les taux actuels de fécondité par âge et rang jusqu’à la fin de leur période féconde. Cette distribution par parité permet de calculer les probabilités d’agrandissement projetées, qui expriment les variations de fécondité implicites dans la combinaison des histoires génésiques jusqu’à ce jour et des taux de fécondité actuels par âge et rang. Un des avantages des probabilités d’agrandissement projetées est qu’il s’agit de ratios, les erreurs dans les taux de fécondité par âge de chaque rang dues à des sous-déclarations tendant à se compenser, quand ces taux sont utilisés pour projeter les probabilités d’agrandissement, à l’exception du passage de la parité nulle à la première naissance.
Nous introduisons deux nouveaux concepts. Le premier, M(i), proportion de femmes ayant atteint la parité i, est la proportion de celles ayant au moins i enfants. Le second est la probabilité d’agrandissement a(i), qui mesure la proportion de femmes qui passent d’une parité i à la suivante, i+1. Les proportions projetées de femmes atteignant la parité i, M*(i), et les probabilités d’agrandissement a*(i) désignent respectivement les proportions de femmes dont on prévoit qu’elles atteindront au moins la parité i, et qu’elles passeront de la parité i à la parité i+1 d’ici à la fin de leur période féconde.
Estimations obtenues
Les mesures suivantes peuvent être calculées pour tout groupe d’âge de femmes :
- La proportion observée de femmes ayant atteint la parité i, 5Mx(i), est la proportion de femmes âgées de x à x+5 qui ont eu i naissances ou plus. La proportion projetée correspondante,, est la proportion de femmes âgées de x à x+5 dont on prévoit qu’elles auront eu i naissances ou plus à la fin de leur vie reproductive. Après la fin de la période féconde, pour x≥50, les proportions observées et attendues sont égales.
- Les probabilités d’agrandissement observées de rang i pour les femmes âgées de x à x+5 sont notées et représentent la proportion de femmes ayant au moins i enfants qui en ont eu au moins un de plus. Les probabilités d’agrandissement projetées sont notées . Une fois encore, pour x≥50, les probabilités observées et attendues sont égales.
Les identités suivantes rattachent ces mesures les unes aux autres et les relient à la distribution des femmes par parité.
Désignons par N(i) le nombre de femmes dans la population de parité exacte i et par N le nombre total de femmes dans la population.
Désignons par W(i) le nombre de femmes dans la population ayant atteint la parité i ou plus et par la parité la plus élevée atteinte dans la population.
Le nombre de femmes qui ont atteint la parité i ou plus est obtenu en sommant les N(i) à partir de i :
de sorte que la proportion correspondante M(i) est égale à
Le nombre de femmes de parité 0 ou plus est
De sorte que la proportion à la parité zéro ou plus, M(0) = N/N = 1.
La parité moyenne dans l’ensemble de la population est
Pour les femmes qui ont achevé leur vie féconde, la parité moyenne est égale à la descendance finale (completed family size, CFS), l’équivalent de l’indice synthétique de fécondité dans une cohorte réelle :
pour x ≥ 50.
Les probabilités d’agrandissement peuvent être écrites en termes de nombres ou de proportions :
Inversement, la proportion de femmes atteignant la parité i+1 ou plus peut être exprimée en termes de probabilités d’agrandissement a(i) pour les transitions aux rangs de naissance inférieurs :
où le symbole désigne un produit.
Données nécessaires et hypothèses
Tableau des données nécessaires
a) Probabilités d’agrandissement observées
- Parité par groupe d’âge des femmes âgées de 45-49 ans ou plus
b) Probabilités d’agrandissement projetées
- Parité par groupe d’âge des femmes âgées de 45-49 ans ou moins, et
- Nombre d’enfants nés au cours de l’année précédant le recensement, classé par âge des mères (en groupes quinquennaux) et par nombre d’enfants déjà nés. Etant donné les hypothèses ci-dessous, une répartition exacte des naissances de la dernière année n’est pas requise. Il est recommandé d’utiliser les naissances de chacun des 12 mois révolus précédant la date du recensement.
Hypothèses importantes
- Les femmes ont eu une naissance au plus au cours de l’année écoulée.
- Les taux de fécondité par âge et rang vont continuer à s’appliquer à l’avenir. Cette hypothèse peut être irréaliste. Elle indique que les probabilités d’agrandissement projetées mesurent les conséquences de la combinaison entre la descendance atteinte par les femmes et les taux de fécondité actuels par âge et rang. Les probabilités d’agrandissement ne doivent pas être traitées comme des prévisions lorsque les cohortes sont encore susceptibles d’avoir encore un nombre important d’enfants additionnels du rang considéré ou lorsque la fécondité connaît une évolution rapide.
Travail préparatoire et recherches préliminaires
Avant d’entreprendre l’analyse des niveaux de fécondité par la méthode des probabilités d’agrandissement, on doit s’interroger sur la qualité des données dans les domaines suivants :
- structure par âge et sexe de la population ;
- naissances déclarées au cours de l’année écoulée ; et
- parités moyennes et nécessité d’une correction d’el Badry.
Précautions et mises en garde
- Si nécessaire, les parités doivent être celles estimées après application de la correction d’el Badry quand des femmes sans enfants ont été considérées à tort comme n’ayant pas déclaré leur parité.
- Si des pondérations liées au plan d’échantillonnage ont été fournies en même temps que les données, elles doivent être appliquées de manière adaptée au logiciel statistique utilisé pour préparer les tableaux nécessaires au modèle.
- Les probabilités d’agrandissement projetées ne doivent être calculées qu’à partir des recensements ou d’autres bases de données incluant un grand nombre de femmes (au moins 10 000 dans chaque groupe d’âge), car le calcul de taux de fécondité par âge et rang fiables (nécessaires à l’établissement des probabilités d’agrandissement projetées) requiert des estimations robustes des taux pour chaque combinaison d’âge et de parité.
Application de la méthode
Le calcul des probabilités d’agrandissement passe par un certain nombre d’étapes, mais le principe qui guide le calcul n’est pas difficile à saisir. Les taux de fécondité par âge et rang qui sont calculés à l’aide des naissances de l’année écoulée servent à projeter la distribution de parité qu’on observerait dans chaque cohorte, si ces taux continuaient à s’appliquer pendant le reste de la période féconde de la cohorte. Ceci est fait en calculant par rang de naissance l’équivalent de l’indice synthétique de fécondité, c’est-à-dire le cumul sur l’ensemble des groupes d’âge des taux de fécondité pour les naissances de rang i. Ces taux servent à calculer les naissances supplémentaires de rang i qui viendraient s’ajouter dans chaque génération de femmes dans l’intervalle entre leur âge actuel et la fin de leur période reproductive. C’est une mesure synthétique du moment car elle cumule les taux d’une période récente. La proportion supplémentaire de femmes qui atteindraient la parité n ou plus est ajoutée à la proportion actuelle de femmes de rang i ou plus ; il en résulte la proportion finale de femmes de parité i ou plus. Ces distributions de parité projetées cumulées servent à calculer les probabilités d’agrandissement projetées, qui permettent l’analyse des tendances de la fécondité. En désignant par 5Px la parité moyenne des femmes âgées entre x et x+5 ans, la descendance finale projetée des femmes âgées de x à x+5 est donc
Rappel :
- PTFR=indice synthétique projeté
- P=parité moyenne (longitudinal)
- TFR=indice synthétique de fécondité (transversal)
- ASFR=taux de fécondité par âge
Etape1 : Elaborer un tableau des enfants déjà nés par groupe d’âge de la mère pour chaque groupe d’âge où des données existent
Classer le nombre de femmes dans chaque groupe d’âge [x, x+5), , par nombre d’enfants déjà nés, i, pour élaborer une série . Si nécessaire, les données doivent avoir été corrigées pour éliminer les parités peu vraisemblables. De même, une correction d’el Badry doit avoir été appliquée.
Etape 2 : Elaborer un tableau du nombre de naissances au cours de l’année écoulée, par âge de la mère et parité
L’hypothèse à ce stade est que les femmes ont eu au maximum un enfant au cours des 12 derniers mois, et qu’elles n’ont eu ni grossesses ni accouchements multiples au cours de la période. Il s’ensuit l’hypothèse implicite qu’une naissance au cours de l’année passée issue d’une femme aujourd’hui de parité i est une naissance de rang i.
Etape 3 : Calculer les proportions de femmes ayant déjà atteint la parité i et les probabilités d’agrandissement pour chaque groupe d’âge
Le nombre de femmes âgées entre x et x+5 qui ont donné naissance à i enfants ou plus est égal à
Les proportions de l’ensemble des femmes âgées de [x, x+5) qui ont eu i naissances ou plus sont calculées ainsi :
Les proportions de femmes avec i naissances ou plus doivent être calculées pour toutes les cohortes, qu’elles aient ou non terminé leur vie féconde. Les femmes de parité zéro doivent être incluses dans le dénominateur, mais pas celles de parité inconnue (après application de la correction d’el Badry, si nécessaire).
La probabilité d’agrandissement entre les parités i et i+1 est alors définie comme
Le calcul des probabilités d’agrandissement pour les femmes qui ont terminé leur vie reproductive s’arrête ici. Les étapes suivantes décrivent comment calculer les probabilités d’agrandissement projetées pour les cohortes de femmes plus jeunes.
Etape 4 : Calculer les taux de fécondité par âge et rang
A partir des tableaux de naissances des 12 derniers mois par groupe d’âge et parité de la mère (étape 2), on calcule les taux de fécondité par âge et rang (en anglais, Age-Order Specific Fertility Rates, AOSFR) des femmes des groupes d’âge 15-19, … 45-49,
Cette fois encore, les femmes de parité non déclarée doivent être exclues du dénominateur. (Le dénominateur étant le nombre total de femmes dans le groupe d’âge (5Nx), et non une exposition au risque de connaître les événements du numérateur, les taux ne sont pas de véritables taux d’incidence, ou taux de 1ère catégorie).
Etape 5 : Calculer les taux de fécondité cumulés par rang
Les taux de fécondité par âge et rang cumulés (en anglais, Total Order Fertility Rates, TOFR) jusqu’à x+5 ans pour le rang i sont calculés ainsi :
Il en résulte que est une mesure de la proportion additionnelle de femmes qui atteindront la parité i entre x+5 ans et la fin de la période reproductive, sous l’hypothèse que la fécondité future restera la même que la fécondité actuelle.
Etape 6 : Calculer la distribution par âge des taux de fécondité par rang et l’interpoler en âges conventionnels
Les taux cumulés calculés à l’étape précédente s’appliquent à 19,5 ans, 24,5 ans, etc. (le décalage d’une demi-année tenant compte du fait que le classement par âge de la mère a été établi à la date du recensement et non à la date de naissance de l’enfant). Par ailleurs, les proportions de femmes ayant atteint chaque parité et les probabilités d’agrandissement s’appliquent (à peu près) au point médian de chaque groupe d’âge 17,5 ans, 22,5 ans, etc. C’est pourquoi les taux par âge et rang doivent être interpolés de sorte qu’ils s’appliquent à l’âge central de chaque groupe d’âge. L’interpolation est réalisée en exprimant les taux de fécondité cumulés par âge et rang comme des proportions des indices synthétiques par rang et en pratiquant une interpolation linéaire sur les gompits des cumulants.
Pour chaque rang de naissance, il faut calculer la proportion de l’indice synthétique par rang réalisée avant d’atteindre la limite supérieure du groupe d’âge. Puisque nous avons utilisé des groupes d’âge décalés dans notre exemple, les limites supérieures sont abaissées d’une demi-année. Les proportions sont calculées en faisant la somme des taux jusqu’à la limite supérieure du groupe d’âge, et en exprimant cette somme en proportion de l’indice synthétique, c’est-à-dire
Comme on l’a déjà dit, ces proportions s’appliquent à 19,5 ans, 24,5 ans, etc. A cause de la courbure du schéma de fécondité, une interpolation linéaire directe pour obtenir les proportions à 22,5 ans, 27,5 ans, etc. n’est pas appropriée. Mais une transformation gompit (double log négatif) fait d’une fonction sigmoïde une droite. Les gompits des proportions sont donc calculés, puis interpolés, avant d’être ramenés à leur échelle originelle par recours aux anti-gompits. Ainsi, en utilisant l’astérisque pour désigner le passage aux points médians conventionnels
(1)
Ceci vaut pour x = 20, 25,…, 40.
Pour éviter d’introduire une composante projetée trop importante dans les probabilités d’agrandissement projetées, nous ne tenons pas compte dans nos calculs des estimations de qui indiquent des proportions de fécondité par rang atteintes au point médian d’un groupe d’âge inférieures à 0,3. Nous traitons comme un peu hasardeux les calculs reposant sur des valeurs de .
Etape 7 : Calculer l’accroissement de parité attendu
La proportion additionnelle des femmes atteignant chaque parité dans l’intervalle entre le point médian du groupe d’âge et la fin de la période féconde est égale à
Etape 8 : Calculer les probabilités d’agrandissement cumulées projetées et les probabilités d’agrandissement projetées
Les probabilités d’agrandissement cumulées projetées sont calculées en ajoutant l’accroissement de parité futur obtenu à la précédente étape aux probabilités d’agrandissement cumulées actuelles obtenues à l’étape 1. La proportion de femmes âgées de x à x+5 ans dont on prévoit qu’elles atteindront au moins la parité i est égale à
Et la probabilité d’agrandissement projetée entre les parités i et i+1 est égale à
Interprétation des résultats
L’interprétation des variations des probabilités d’agrandissement peut être compliquée par des erreurs dans les données et doit tenir compte des hypothèses qui sous-tendent les calculs. S’il y a des erreurs dans les données, il est prudent de ne pas sur-interpréter les résultats. Les probabilités d’agrandissement qui incluent une proportion substantielle de composante projetée doivent être interprétées avec une prudence redoublée, car elles risquent de refléter des effets de période qui cesseront à l’avenir. Si par exemple les taux de fécondité par âge et rang reflètent un retard des naissances dans la période ou les données sont recueillies, et que la fécondité s’accroit ensuite par compensation, de sorte que les femmes retrouvent les parités atteintes par les cohortes antérieures, les probabilités d’agrandissement projetées seront trompeuses. De même, un déclin futur de la fécondité réduira les parités finales des femmes même si les taux actuels prédisent une stabilité. Les probabilités d’agrandissement projetées pour les femmes âgées sont plus fiables car elles incluent une part plus faible de fécondité projetée.
La probabilité projetée de premier rang, , est souvent biaisée du fait d’erreurs sur la période de référence qui ne sont pas compensées comme elles le sont pour les probabilités des autres rangs. Les proportions projetées de femmes ayant au moins un enfant sont affectées par les modifications de l’âge à la première naissance. La mesure étant prise dans une cohorte fictive à partir des taux du moment, des variations dans le calendrier des premières naissances affectent aussi le taux cumulé, qui peut prendre une valeur extérieure à l’intervalle des valeurs attendues pour la plupart des cohortes réelles dans les pays en développement. Du fait de fluctuations de court terme et d’effets de calendrier, la probabilité de premier rang (du moment) peut éventuellement dépasser l’unité. Ceci ne doit pas être confondu avec, ou interprété comme, une probabilité d’agrandissement supérieure à 1, ce qui est par définition impossible.
La probabilité de premier rang projetée peut aussi donner une indication sur la qualité des données. Les taux indiquent la proportion de femmes dont on prévoit qu’elles deviendront mères au cours de leur vie reproductive, dans une cohorte fictive soumise à ces taux. Des erreurs sur la période de référence peuvent se traduire par une proportion invraisemblable de femmes dont on prévoit qu’elles deviendront mères. Dans des cas extrêmes d’erreurs, la proportion peut dépasser éventuellement l’unité. Des taux cumulées inférieurs à 0,9 laissent présumer des erreurs dans les données ou des variations importantes dans le calendrier des premières naissances, mais on a pu observer de telles valeurs dans des populations affectées par des niveaux élevés de stérilité primaire et dans des populations actuelles où l’infécondité volontaire est fréquente. On a souvent observé une hausse de la proportion (projetée) de femmes dont on s’attend à ce qu’elles deviennent mères, , dans les populations qui ont connu un recul de la stérilité primaire.
Les probabilités d’agrandissement de rang plus élevé peuvent être sujettes à de fortes fluctuations dues à des erreurs d’échantillonnage dans les taux de fécondité par âge et rang, ceux-ci étant calculés sur des nombres de naissances relativement faibles. Quand d’importantes erreurs d’échantillonnage sont dues aux faibles nombres de femmes, on peut envisager de faire la moyenne de probabilités d’agrandissement projetées contiguës – deux ou plus – afin de percevoir les tendances plus clairement.
L’examen de l’évolution des probabilités d’agrandissement au fil des cohortes (projetées pour les cohortes de femmes âgées de 40-44 ans et moins et effectives pour les cohortes de 45-49 ans et plus) peut éclairer les tendances de la fécondité. Le recul d’une probabilité d’agrandissement (projetée) indique un recul de la proportion de femmes ayant une naissance supplémentaire et, toutes choses égales par ailleurs, une baisse de la fécondité. Des variations des probabilités d’agrandissement à différentes parités peuvent tenir à divers facteurs, certaines probabilités étant affectées davantage que d’autres. Identifier celles qui varient peut être utile pour comprendre les modifications de la fécondité dans la population. Par exemple, la diffusion de la limitation des naissances par une contraception liée à la parité se traduira par un recul des probabilités d’agrandissement à des parités moyennes (disons, 3 à 6). Une variation des probabilités d’agrandissement à des rangs plus élevés reflète souvent des variations de fécondité indépendantes de la parité, par exemple des modifications de la durée d’allaitement.
Exemple
Nous analysons les données du recensement de 1998 au Cambodge réalisé le 3 mars 1998. La méthode est présentée dans le fichier Excel joint.
Etape1 : Elaborer un tableau des enfants déjà nés par groupe d’âge de la mère pour chaque groupe d’âge où des données existent
Les données du recensement, non corrigées, figurent au tableau 1.
Tableau 1 Nombre de femmes par groupe d’âge et parité, Cambodge, recensement de 1998.
Groupe d’âge | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Parité (i) | 15-19 | 20-24 | 25-29 | 30-34 | 35-39 | 40-44 | 45-49 | 50-54 | 55-59 | 60-64 |
0 | 635 940 | 200 620 | 105 350 | 55 300 | 33 900 | 22 970 | 16 430 | 9 790 | 7 640 | 6 880 |
1 | 30 340 | 94 810 | 79 570 | 38 780 | 21 150 | 16 570 | 13 460 | 9 600 | 8 020 | 7 450 |
2 | 5 980 | 62 580 | 113 640 | 66 750 | 33 320 | 21 920 | 17 220 | 12 840 | 9 690 | 8 020 |
3 | 1 650 | 21 680 | 88 750 | 75 660 | 45 680 | 27 750 | 20 250 | 15 170 | 11 180 | 8 120 |
4 | 1 200 | 6 890 | 44 480 | 72 370 | 56 100 | 35 450 | 24 530 | 18 090 | 13 350 | 10 160 |
5 | 630 | 2 060 | 16 580 | 51 600 | 57 050 | 39 100 | 26 660 | 19 660 | 16 100 | 12 040 |
6 | 0 | 1 120 | 5 630 | 30 250 | 50 960 | 39 180 | 27 540 | 19 860 | 16 180 | 12 250 |
7 | 0 | 510 | 2 110 | 13 390 | 35 780 | 33 190 | 25 850 | 18 880 | 16 170 | 13 690 |
8 | 0 | 480 | 1 070 | 5 970 | 20 580 | 24 920 | 23 180 | 16 940 | 14 830 | 11 970 |
9 | 0 | 0 | 440 | 1 820 | 9 590 | 15 860 | 16 130 | 12 680 | 11 360 | 9 200 |
10 | 0 | 0 | 240 | 880 | 4 840 | 10 420 | 12 790 | 10 720 | 9 800 | 7 750 |
11 | 0 | 0 | 120 | 320 | 1 760 | 4 430 | 6 670 | 5 370 | 4 850 | 3 970 |
12 | 0 | 0 | 80 | 150 | 760 | 3 220 | 5 350 | 4 810 | 4 780 | 4 230 |
13 | 0 | 0 | 40 | 60 | 250 | 990 | 1 960 | 1 790 | 1 790 | 1 440 |
14 | 0 | 0 | 0 | 40 | 170 | 620 | 1 020 | 970 | 760 | 540 |
15 | 0 | 0 | 0 | 10 | 10 | 250 | 510 | 460 | 440 | 490 |
16 | 0 | 0 | 0 | 10 | 30 | 130 | 230 | 160 | 140 | 210 |
17 | 0 | 0 | 0 | 0 | 10 | 40 | 80 | 50 | 70 | 70 |
18 | 0 | 0 | 0 | 10 | 10 | 30 | 30 | 30 | 40 | 40 |
TOTAL | 675 740 | 390 750 | 458 100 | 413 370 | 371 950 | 297 040 | 239 890 | 177 870 | 147 190 | 118 520 |
Parité moyenne | 0,082 | 0,862 | 1,965 | 3,150 | 4,369 | 5,086 | 5,566 | 5,758 | 5,974 | 5,969 |
Les données suivent un schéma classique d’augmentation des parités moyennes avec l’âge jusqu’à 45-49 ans. Par la suite, les parités moyennes n’augmentent que légèrement. Les données indiquent donc que les femmes de plus de 50 ans ont omis de déclarer certains de leurs enfants déjà nés ou que la fécondité a été à peu près constante parmi les femmes ayant terminé leur vie féconde dans les 10-15 dernières années.
Etape 2 : Elaborer un tableau du nombre de naissances au cours de l’année écoulée, par âge de la mère et parité
Les données du recensement de 1998 au Cambodge sur le nombre d’enfants nés au cours de l’année précédant le recensement, par groupe d’âge de la mère et parité, figurent au tableau 2.
Tableau 2 Naissances déclarées au cours de l’année précédant le recensement par groupe d’âge de la mère et parité, Cambodge, recensement de 1998.
| Groupe d’âge | ||||||
|---|---|---|---|---|---|---|---|
Parité (i) | 15-19 | 20-24 | 25-29 | 30-34 | 35-39 | 40-44 | 45-49 |
0 | |||||||
1 | 13 100 | 23 490 | 11 500 | 3 170 | 1 040 | 320 | 190 |
2 | 2 340 | 19 180 | 21 320 | 7 830 | 2 010 | 730 | 150 |
3 | 410 | 8 370 | 22 640 | 11 470 | 3 790 | 850 | 230 |
4 | 210 | 2 430 | 14 330 | 14 110 | 5 200 | 1 450 | 300 |
5 | 100 | 600 | 6 220 | 12 440 | 6 740 | 1 830 | 480 |
6 | 0 | 280 | 2 020 | 8 360 | 8 120 | 2 870 | 560 |
7 | 0 | 90 | 750 | 4 430 | 7 220 | 3 240 | 840 |
8 | 0 | 90 | 360 | 2 100 | 4 930 | 3 020 | 750 |
9 | 0 | 0 | 90 | 640 | 2 800 | 2 310 | 690 |
10 | 0 | 0 | 40 | 300 | 1 390 | 1 570 | 640 |
11 | 0 | 0 | 30 | 160 | 630 | 810 | 490 |
12 | 0 | 0 | 10 | 40 | 200 | 480 | 320 |
13 | 0 | 0 | 10 | 20 | 80 | 250 | 140 |
14 |
| 0 | 0 | 10 | 60 | 100 | 70 |
15 |
|
| 0 | 0 | 0 | 50 | 30 |
16 |
|
|
| 0 | 10 | 10 | 30 |
17 |
|
|
|
| 0 | 0 | 10 |
18 |
|
|
| 0 | 0 | 0 | 10 |
Taux de fécondité par âge | 0,024 | 0,140 | 0,173 | 0,157 | 0,119 | 0,067 | 0,025 |
D’après les données, l’indice synthétique de fécondité est de l’ordre de 3,25 enfants par femmes, soit nettement moins que la descendance finale (5,566) de la génération des femmes âgées de 45-49 ans. Ceci suggère soit une baisse rapide de la fécondité encours dans le pays, soit une omission systématique des naissances récentes dans le recensement.
Etape 3 : Calculer les proportions de femmes ayant déjà atteint la parité i et les probabilités d’agrandissement pour chaque groupe d’âge
Les proportions de femmes atteignant la parité i ou plus sont calculées à partir des données du tableau 1 et figurent au tableau 3. Les parités supérieures ou égales à 12 sont regroupées.
Tableau 3 Proportion de femmes ayant atteint chaque parité par groupe d’âge, Cambodge, recensement de 1998
| Groupe d’âge | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
Parité (i) | 15-19 | 20-24 | 25-29 | 30-34 | 35-39 | 40-44 | 45-49 | 50-54 | 55-59 | 60-64 |
0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
1 | 0,0589 | 0,4866 | 0,7700 | 0,8662 | 0,9089 | 0,9227 | 0,9315 | 0,9450 | 0,9481 | 0,9420 |
2 | 0,0140 | 0,2439 | 0,5963 | 0,7724 | 0,8520 | 0,8669 | 0,8754 | 0,8910 | 0,8936 | 0,8791 |
3 | 0,0051 | 0,0838 | 0,3483 | 0,6109 | 0,7624 | 0,7931 | 0,8036 | 0,8188 | 0,8278 | 0,8114 |
4 | 0,0027 | 0,0283 | 0,1545 | 0,4279 | 0,6396 | 0,6997 | 0,7192 | 0,7335 | 0,7518 | 0,7429 |
5 | 0,0009 | 0,0107 | 0,0574 | 0,2528 | 0,4888 | 0,5803 | 0,6169 | 0,6318 | 0,6611 | 0,6572 |
6 | 0,0000 | 0,0054 | 0,0212 | 0,1280 | 0,3354 | 0,4487 | 0,5058 | 0,5213 | 0,5517 | 0,5556 |
7 | 0,0000 | 0,0025 | 0,0090 | 0,0548 | 0,1984 | 0,3168 | 0,3910 | 0,4096 | 0,4418 | 0,4522 |
8 | 0,0000 | 0,0012 | 0,0043 | 0,0224 | 0,1022 | 0,2051 | 0,2833 | 0,3035 | 0,3320 | 0,3367 |
9 | 0,0000 | 0,0000 | 0,0020 | 0,0080 | 0,0469 | 0,1212 | 0,1866 | 0,2082 | 0,2312 | 0,2357 |
10 | 0,0000 | 0,0000 | 0,0010 | 0,0036 | 0,0211 | 0,0678 | 0,1194 | 0,1370 | 0,1540 | 0,1581 |
11 | 0,0000 | 0,0000 | 0,0005 | 0,0015 | 0,0081 | 0,0327 | 0,0661 | 0,0767 | 0,0874 | 0,0927 |
12+ | 0.0000 | 0,0000 | 0,0003 | 0,0007 | 0,0033 | 0,0178 | 0,0383 | 0,0465 | 0,0545 | 0,0592 |
La proportion des femmes ayant eu i naissances ou plus figure au tableau 3. Ainsi, alors que 80,4 % des femmes âgées de 45-49 ans ont eu au moins trois naissances, elles ne sont que 71,9 % à en avoir eu quatre ou plus. Les probabilités d’agrandissement qui en découlent, , figurent au tableau 4.
Tableau 4 Probabilités d’agrandissement observées par groupe d’âge de la mère et parité, Cambodge, recensement de 1998
| Groupe d’âge | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
Parité (i) | 15-19 | 20-24 | 25-29 | 30-34 | 35-39 | 40-44 | 45-49 | 50-54 | 55-59 | 60-64 |
0 | 0,0589 | 0,4866 | 0,7700 | 0,8662 | 0,9089 | 0,9227 | 0,9315 | 0,9450 | 0,9481 | 0,9420 |
1 | 0,2377 | 0,5013 | 0,7744 | 0,8917 | 0,9374 | 0,9395 | 0,9398 | 0,9429 | 0,9425 | 0,9333 |
2 | 0,3679 | 0,3435 | 0,5840 | 0,7909 | 0,8949 | 0,9149 | 0,9180 | 0,9190 | 0,9263 | 0,9230 |
3 | 0,5259 | 0,3378 | 0,4437 | 0,7004 | 0,8389 | 0,8822 | 0,8950 | 0,8958 | 0,9082 | 0,9156 |
4 | 0,3443 | 0,3770 | 0,3717 | 0,5909 | 0,7642 | 0,8294 | 0,8578 | 0,8613 | 0,8794 | 0,8846 |
5 | 0,0000 | 0,5060 | 0,3698 | 0,5063 | 0,6862 | 0,7732 | 0,8199 | 0,8251 | 0,8345 | 0,8454 |
6 | 0,4692 | 0,4214 | 0,4283 | 0,5915 | 0,7060 | 0,7730 | 0,7858 | 0,8008 | 0,8140 | |
7 | 0,4848 | 0,4854 | 0,4091 | 0,5151 | 0,6473 | 0,7244 | 0,7409 | 0,7513 | 0,7446 | |
8 | 0,0000 | 0,4623 | 0,3560 | 0,4586 | 0,5909 | 0,6589 | 0,6862 | 0,6965 | 0,7001 | |
9 | 0,5217 | 0,4485 | 0,4498 | 0,5593 | 0,6397 | 0,6577 | 0,6662 | 0,6707 | ||
10 | 0,5000 | 0,4054 | 0,3827 | 0,4824 | 0,5534 | 0,5599 | 0,5677 | 0,5864 | ||
11 | 0,5000 | 0,4667 | 0,4133 | 0.5438 | 0,5792 | 0,6063 | 0,6232 | 0,6388 | ||
Environ 93,2 % des femmes âgées de 45-49 ans au Cambodge en 1998 ont eu au moins un enfant et 89,5 % des mères de trois enfants dans le même groupe d’âge en ont ensuite eu un quatrième.
Etape 4 : Calculer les taux de fécondité par âge et rang
Les naissances déclarées au cours de l’année passée (par âge et parité) du tableau 2 sont divisées par le nombre total de femmes dans chaque groupe d’âge (les totaux par groupe d’âge du tableau 1). Les taux de fécondité par âge et rang qui en résultent figurent au tableau 5. Par exemple 5AOSFR25(1) = 11 500/458 100 = 0,0251.
Tableau 5 Taux de fécondité par âge et rang et indice synthétique de fécondité par rang (TOFR), Cambodge, recensement de 1998.
| Groupe d’âge | |||||||
|---|---|---|---|---|---|---|---|---|
Parité (i) | 15-19 | 20-24 | 25-29 | 30-34 | 35-39 | 40-44 | 45-49 | TOFR(i) |
0 | ||||||||
1 | 0,0194 | 0,0601 | 0,0251 | 0,0077 | 0,0028 | 0,0011 | 0,0008 | 0,5847 |
2 | 0,0035 | 0,0491 | 0,0465 | 0,0189 | 0,0054 | 0,0025 | 0,0006 | 0,6326 |
3 | 0,0006 | 0,0214 | 0,0494 | 0,0277 | 0,0102 | 0,0029 | 0,0010 | 0,5660 |
4 | 0,0003 | 0,0062 | 0,0313 | 0,0341 | 0,0140 | 0,0049 | 0,0013 | 0,4603 |
5 | 0,0001 | 0,0015 | 0,0136 | 0,0301 | 0,0181 | 0,0062 | 0,0020 | 0,3582 |
6 | 0,0000 | 0,0007 | 0,0044 | 0,0202 | 0,0218 | 0,0097 | 0,0023 | 0,2959 |
7 | 0,0000 | 0,0002 | 0,0016 | 0,0107 | 0,0194 | 0,0109 | 0,0035 | 0,2320 |
8 | 0,0000 | 0,0002 | 0,0008 | 0,0051 | 0,0133 | 0,0102 | 0,0031 | 0,1632 |
9 | 0,0000 | 0,0000 | 0,0002 | 0,0015 | 0,0075 | 0,0078 | 0,0029 | 0,0996 |
10 | 0,0000 | 0,0000 | 0,0001 | 0,0007 | 0,0037 | 0,0053 | 0,0027 | 0,0625 |
11 | 0,0000 | 0,0000 | 0,0001 | 0,0004 | 0,0017 | 0,0027 | 0,0020 | 0,0346 |
12+ | 0,0000 | 0,0000 | 0,0000 | 0,0002 | 0,0009 | 0,0030 | 0,0025 | 0,0335 |
Taux de fécondité par âge | 0,0239 | 0,1396 | 0,1731 | 0,1574 | 0,1189 | 0,0670 | 0,0247 | 3,5231 |
Etape 5 : Calculer les taux de fécondité cumulés par rang
A partir des données présentées au tableau 5, on obtient les taux de fécondité par âge et rang cumulés en sommant sur chaque ligne jusqu’au groupe d’âge désiré. Par exemple, le taux par âge et rang cumulé jusqu’à la fin du groupe des 25-29 ans pour la parité 3 est égale à 5 x (0,0006 + 0,0214 + 0,0494)=0,3572.
Etape 6 : Calculer la distribution par âge des taux de fécondité par rang et l’interpoler en âges conventionnels
A partir des résultats de l’étape 5, la proportion de fécondité par rang atteinte à l’issue de chaque groupe d’âge est obtenue en divisant les taux de fécondité par rang cumulés par l’indice synthétique de fécondité par rang qui figure dans la dernière colonne du tableau 5. Les résultats sont au tableau 6.
Tableau 6 Proportion de la fécondité par rang atteinte à l’issue de chaque groupe d’âge, Cambodge, recensement de 1998.
| Groupe d’âge | ||||||
|---|---|---|---|---|---|---|---|
Parité (i) | 19,5 | 24,5 | 29,5 | 34,5 | 39,5 | 44,5 | 49,5 |
0 |
| ||||||
1 | 0,1658 | 0,6799 | 0,8945 | 0,9601 | 0,9840 | 0,9932 | 1,0000 |
2 | 0,0274 | 0,4153 | 0,7832 | 0,9329 | 0,9756 | 0,9951 | 1,0000 |
3 | 0,0054 | 0,1946 | 0,6311 | 0,8762 | 0,9663 | 0,9915 | 1,0000 |
4 | 0,0034 | 0,0709 | 0,4107 | 0,7815 | 0,9334 | 0,9864 | 1,0000 |
5 | 0,0021 | 0,0235 | 0,2130 | 0,6331 | 0,8861 | 0,9721 | 1,0000 |
6 | 0,0000 | 0,0121 | 0,0866 | 0,4284 | 0,7973 | 0,9606 | 1,0000 |
7 | 0,0000 | 0,0050 | 0,0402 | 0,2712 | 0,6895 | 0,9245 | 1,0000 |
8 | 0,0000 | 0,0071 | 0,0311 | 0,1868 | 0,5928 | 0,9042 | 1,0000 |
9 | 0,0000 | 0,0000 | 0,0099 | 0,0876 | 0,4654 | 0,8556 | 1,0000 |
10 | 0,0000 | 0,0000 | 0,0070 | 0,0650 | 0,3639 | 0,7866 | 1,0000 |
11 | 0,0000 | 0,0000 | 0,0095 | 0,0654 | 0,3103 | 0,7046 | 1,0000 |
12+ | 0,0000 | 0,0000 | 0,0065 | 0,0318 | 0,1724 | 0,6201 | 1,0000 |
La proportion de la fécondité atteinte à 49,5 ans est supposée égale à un. Avec le même exemple qu’à l’étape précédente, la proportion de fécondité de troisième rang atteinte à 29,5 ans est 0,3572/0,5660=0,6311.
Les âges des mères étant ceux au moment du recensement, et les parités moyennes calculées à l’étape 1 s’appliquant à 17,5 ans, 22,5 ans etc., nous devons rendre les deux séries de données comparables en interpolant entre deux valeurs pour avoir des proportions à 22,5 ans, 27, 5 ans etc. la formule est donnée par l’équation 1 et les résultats figurent au tableau 7.
Etant donné l’incertitude entourant la projection des probabilités d’agrandissement futures, les cellules du tableau 7 dont les valeurs sont inférieures à 0,3 (c’est-à-dire où moins de 30 % de la fécondité par rang a été atteinte à l’âge indiqué) sont indiquées en rouge et seront exclues des calculs ultérieurs. Les valeurs supérieures à 0,3 mais inférieures à 0,5 sont indiquées en bleu et doivent être traitées avec circonspection dans les calculs ultérieurs. Les calculs reposant sur ces valeurs seront présentés entre parenthèses dans les tableaux suivants.
Tableau 7 Proportion de fécondité par rang atteinte au point médian de chaque intervalle d’âge, Cambodge, recensement de 1998.
| Groupe d’âge | |||||
|---|---|---|---|---|---|---|
Parité (i) | 22,5 | 27,5 | 32,5 | 37,5 | 42,5 | 47,5 |
1 | 0,4897 | 0,8326 | 0,9409 | 0,9769 | 0,9904 | 0,9999 |
2 | 0,2135 | 0,6652 | 0,8915 | 0,9634 | 0,9906 | 0,9999 |
3 | 0,0739 | 0,4655 | 0,8044 | 0,9428 | 0,9852 | 0,9999 |
4 | 0.0275 | 0,2526 | 0,6624 | 0,8916 | 0,9742 | 0,9998 |
5 | 0,0102 | 0,1104 | 0,4751 | 0,8139 | 0,9506 | 0,9998 |
6 |
| 0,0452 | 0,2738 | 0,6811 | 0,9228 | 0,9997 |
7 |
| 0,0197 | 0.1539 | 0,5410 | 0,8640 | 0,9996 |
8 |
| 0,0183 | 0.1061 | 0,4345 | 0,8232 | 0,9996 |
9 |
| 0,0430 | 0,2965 | 0,7449 | 0,9995 | |
10 |
| 0,0311 | 0,2221 | 0,6527 | 0,9994 | |
11 |
| 0,0341 | 0,1937 | 0,5671 | 0,9993 | |
12+ |
| 0,0181 | 0,1001 | 0,4473 | 0,9993 | |
Etape 7 : Calculer l’accroissement de parité attendu
La proportion additionnelle des femmes atteignant chaque parité dans l’intervalle entre le point médian du groupe d’âge et la fin de la période féconde est donnée par
comme le montre le tableau 8.
Tableau 8 Proportion additionnelle de femmes atteignant la parité i d’ici la fin de la période féconde par groupe d’âge de la mère, Cambodge, recensement de 1998.
Parité (i) | 22,5 | 27,5 | 32,5 | 37,5 | 42,5 |
|---|---|---|---|---|---|
0 | |||||
1 | (0,2984) | 0,0979 | 0,0346 | 0,0135 | 0,0056 |
2 | 0,2118 | 0,0686 | 0,0232 | 0,0059 | |
3 | (0,3025) | 0,1107 | 0,0324 | 0,0084 | |
4 | 0,1554 | 0,0499 | 0,0119 | ||
5 | (0,1880) | 0,0666 | 0,0177 | ||
6 | 0,0944 | 0,0228 | |||
7 | 0,1065 | 0,0316 | |||
8 | (0,0923) | 0,0289 | |||
9 | 0,0254 | ||||
10 | 0,0217 | ||||
11 | 0,0150 | ||||
12+ | (0,0185) |
Ainsi, l’accroissement futur de fécondité de rang 3 prévu après 30 ans est égal à 0,5660 x (1 – 0,4655) = 0,3025. Les valeurs entre parenthèses sont moins fiables, étant fondées sur des proportions de fécondité par âge et rang atteintes au point médian de ce groupe d’âge inférieures à 0,50.
Etape 8 : Calculer les probabilités d’agrandissement cumulées projetées et les probabilités d’agrandissement projetées
Les probabilités d’agrandissement cumulées projetées sont obtenues en additionnant les accroissements futurs de fécondité par rang présentés au tableau 8 à la proportion de femmes ayant atteint chacune des parités telle que calculée à l’étape 3 et présentée au tableau 3.
Les probabilités d’agrandissement projetées pour les cohortes encore en âge d’avoir des enfants peuvent maintenant être comparées aux probabilités d’agrandissement finales des femmes âgées de 50 ans ou plus. Les résultats figurent au tableau 10.
Tableau 9 Proportions projetées devant atteindre chaque parité, Cambodge, recensement de 1998
| Groupe d’âge | ||||||||
|---|---|---|---|---|---|---|---|---|---|
Parité (i) | 20-24 | 25-29 | 30-34 | 35-39 | 40-44 | 45-49 | 50-54 | 55-59 | 60-64 |
0 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
1 | (0,7850) | 0,8679 | 0,9008 | 0,9224 | 0,9283 | 0,9315 | 0,9450 | 0,9481 | 0,9420 |
2 | 0,8081 | 0,8410 | 0,8752 | 0,8728 | 0,8754 | 0,8910 | 0,8936 | 0,8791 | |
3 | (0,6508) | 0,7216 | 0,7948 | 0,8014 | 0,8036 | 0,8188 | 0,8278 | 0,8114 | |
4 | 0,5833 | 0,6895 | 0,7115 | 0,7192 | 0,7335 | 0,7518 | 0,7429 | ||
5 | (0,4408) | 0,5554 | 0,5980 | 0,6169 | 0,6318 | 0,6611 | 0,6572 | ||
6 | 0,4298 | 0,4715 | 0,5058 | 0,5213 | 0,5517 | 0,5556 | |||
7 | 0,3049 | 0,3483 | 0,3910 | 0,4096 | 0,4418 | 0,4522 | |||
8 | (0,1945) | 0,2339 | 0,2833 | 0,3035 | 0,3320 | 0,3367 | |||
9 | 0,1466 | 0,1866 | 0,2082 | 0,2312 | 0,2357 | ||||
10 | 0,0895 | 0,1194 | 0,1370 | 0,1540 | 0,1581 | ||||
11 | 0,0477 | 0,0661 | 0,0767 | 0,0874 | 0,0927 | ||||
12+ | (0,0363) | 0,0383 | 0,0465 | 0,0545 | 0,0592 | ||||
Dans le groupe d’âge 25-29 ans, la proportion projetée avec une parité 3 et plus est de 0,3483 (cf. tableau 3) + 0,3025 (cf. tableau 8) = 0,6508. Les valeurs entre parenthèses sont moins fiables, étant fondées sur des proportions de fécondité par âge et rang atteintes au point médian de ce groupe d’âge inférieures à 0,50.
Les probabilités d’agrandissement projetées sont calculées en divisant les proportions devant atteindre chaque parité successive dans une cohorte d’âge (Tableau 10).
Tableau 10 Probabilités d’agrandissement projetées, Cambodge, recensements de 1998
| Groupe d’âge | ||||||||
|---|---|---|---|---|---|---|---|---|---|
Parité (i) | 20-24 | 25-29 | 30-34 | 35-39 | 40-44 | 45-49 | 50-54 | 55-59 | 60-64 |
0 | (0,7850) | 0,8679 | 0,9008 | 0,9224 | 0,9283 | 0,9315 | 0,9450 | 0,9481 | 0,9420 |
1 | 0,9312 | 0,9337 | 0,9488 | 0,9403 | 0,9398 | 0,9429 | 0,9425 | 0,9333 | |
2 | (0,8053) | 0,8580 | 0,9081 | 0,9182 | 0,9180 | 0,9190 | 0,9263 | 0,9230 | |
3 | 0,8083 | 0,8676 | 0,8878 | 0,8950 | 0,8958 | 0,9082 | 0,9156 | ||
4 | (0.7558) | 0,8055 | 0,8404 | 0,8578 | 0,8613 | 0,8794 | 0,8846 | ||
5 | 0,7738 | 0,7885 | 0,8199 | 0,8251 | 0,8345 | 0,8454 | |||
6 | 0,7094 | 0,7388 | 0,7730 | 0,7858 | 0,8008 | 0,8140 | |||
7 | (0,6379) | 0,6715 | 0,7244 | 0,7409 | 0,7513 | 0,7446 | |||
8 | 0,6266 | 0,6589 | 0,6862 | 0,6965 | 0,7001 | ||||
9 | 0,6104 | 0,6397 | 0,6577 | 0,6662 | 0,6707 | ||||
10 | 0,5326 | 0,5534 | 0,5599 | 0,5677 | 0,5864 | ||||
11 | (0,7611) | 0,5792 | 0,6063 | 0,6232 | 0,6388 | ||||
Probabilités d’agrandissement projetées
La probabilité d’agrandissement de la parité 0 à la parité 1 indique la proportion de femmes ayant eu au moins un enfant. La probabilité d’agrandissement projetée souffre d’un fort biais, comme nous le verrons plus loin. La proportion de femmes sans enfants est restée à peu près constante au fil des cohortes. Mais on voit à la figure 1 que les probabilités d’agrandissement aux parités 2 et suivantes reculent sensiblement dans les cohortes successives.

Les proportions projetées de femmes qui devraient atteindre chaque parité d’après le recensement de 1998 au Cambodge sont représentées à la figure 2.
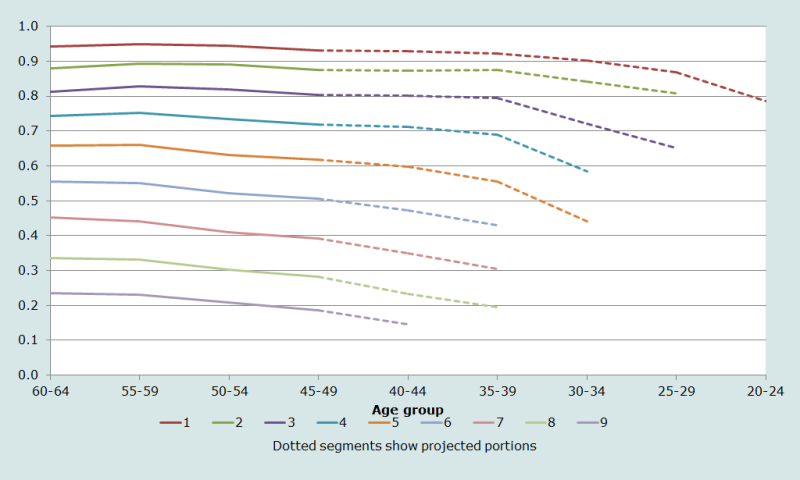
Les conséquences de probabilités d’agrandissement réduites dans les cohortes jeunes apparaissent sur les proportions de femmes qui devraient atteindre chaque parité. Alors que 55 % des femmes âgées de 60-64 ans ont eu 6 enfants ou plus, cette proportion dépasse à peine la moitié (50,6 %) dans la cohorte dont la période féconde vient de se terminer (femmes âgées de 45-49 ans).
On voit ici les prémices d’une baisse de la fécondité qui a débuté lorsque la cohorte aujourd’hui âgée de 50-54 ans a eu ses enfants, soit environ 25-30 ans avant le recensement.
Première maternité
D’après les données cambodgiennes, la proportion des femmes de 45-49 ans ayant eu au moins un enfant était de 0,9315. Les proportions projetées, classées selon l’âge actuel de la mère, figurent à la première ligne du tableau 10.
Il y a certainement eu d’importants changements dans le calendrier de la première maternité dans les cohortes jeunes, mais les résultats pour les femmes entre 20 et 30 ans ainsi que, très probablement, pour celles âgées de 30-34 ans, sont invraisemblables pour des raisons déjà évoquées dans la présentation de leur mode de calcul. Les probabilités d’agrandissement projetées pour les femmes entre 20 et 30 ans sont fortement affectées à la fois par des modifications dans le calendrier de la fécondité et par l’importance de la composante projetée. Ces résultats ne doivent pas être pris en compte ; une mesure de la première maternité par la méthode des tables de survie doit leur être préférée. Mais ces méthodes et leurs applications débordent des objectifs de ce manuel.
A l’exception de cet indice, le calcul des probabilités d’agrandissement projetées doit éliminer l’effet des erreurs sur la période de référence dans la mesure où celles-ci sont indépendantes de la parité. On le voit dans les estimations des probabilités d’agrandissement projetées pour les autres parités.
Les données pour les cohortes âgées de 20-24 à 40-44 ans incluent une composante projetée d’autant plus importante que la cohorte est jeune. Les données des cohortes plus âgées reflètent une fécondité achevée. Les probabilités d’agrandissement projetées pour les femmes de 30-44 ans font apparaître un recul systématique de la proportion de femmes qui devraient atteindre la parité suivante d’ici à la fin de leur période féconde. C’est le signe d’un processus en cours de baisse de la fécondité.
Autres lectures et références
On trouvera dans Brass and Juárez (1983) l’exposé de méthodes semblables à celles présentées ci-dessus, mais utilisant les données détaillées d’histoires génésiques et accordant davantage d’attention aux effets de censure et de sélection.
De nombreux travaux portent sur l’utilisation et les problèmes associés aux probabilités d’agrandissement du moment (par opposition aux mesures prises dans les cohortes). Ceci déborde des objectifs du présent manuel. Le lecteur intéressé peut consulter Whelpton (1946), Feeney and Yu (1987), Ní Bhrolcháin (1987), Hinde (1998), et Bongaarts and Feeney (1998).
Bongaarts J and G Feeney. 1998. "On the quantum and tempo of fertility", Population and Development Review 24(2):271-291. doi: https://dx.doi.org/10.2307/2807974
Brass W. 1985. Advances in Methods for Estimating Fertility and Mortality from Limited and Defective Data. London: Centre for Population Studies, London School of Hygiene and Tropical Medicine.
Brass W and F Juárez. 1983. "Censored cohort parity progression ratios from birth histories", Asian and Pacific Census Forum 10(1):5-12. https://hdl.handle.net/10125/3583
Feeney G and J Yu. 1987. "Period parity progression measures of fertility in China", Population Studies 41(1):77-102. doi: https://dx.doi.org/10.1080/0032472031000142546
Hinde A. 1998. Demographic Methods. London: Arnold
Ní Bhrolcháin M. 1987. "Period parity progression ratios and birth intervals in England and Wales, 1941-1971: A synthetic life table analysis", Population Studies 41(1):103-125. doi: https://dx.doi.org/10.1080/0032472031000142556
Preston SH, P Heuveline and M Guillot. 2001. Demography: Measuring and Modelling Population Processes. Oxford: Blackwell.
Whelpton PK. 1946. "Reproduction rates adjusted for age, parity, fecundity, and marriage", Journal of the American Statistical Association 41(236):501-516. doi: https://dx.doi.org/10.1080/01621459.1946.10501893
- Printer-friendly version
- Log in to post comments
