Estimation directe de la fécondité à partir de données d’enquêtes contenant des histoires génésiques
Description de la méthode
L’estimation directe de la fécondité (taux par âge et indice synthétique) à partir de données d’enquêtes contenant des histoires génésiques est relativement simple. Si les données sont recueillies soigneusement à l’aide d’un instrument validé (comme celui utilisé dans les Enquêtes Démographiques et de Santé), elles peuvent fournir des estimations de fécondité fiables et précises. Elles sont cependant souvent soumises à des déformations, en particulier dues au report des naissances vers des périodes plus anciennes afin d’éviter de répondre à des questions supplémentaires, par exemple sur la santé des enfants ou l’anthropométrie (Cleland 1996). Ces problèmes ont été à nouveau mis en évidence récemment par Schoumaker (2010, 2011). La mauvaise datation des naissances et leur omission peuvent entrainer une sous-estimation de la fécondité (en particulier dans la période de trois à cinq ans avant l’enquête).
Il existe deux façons d’estimer la fécondité directement à partir des données des histoires génésiques détaillées. La première – utilisée par les EDS dans leurs rapports officiels – consiste à produire une estimation couvrant une période d’un ou de trois ans avant l’enquête. (La période de trois ans est souvent préférée pour éviter des fluctuations dans les estimations dues au nombre relativement faible de naissances annuelles dans les EDS). La méthode est décrite en détail dans le Guide des statistiques des EDS (en anglais) (Rutstein and Rojas 2003). Elle présente deux inconvénients. D’une part, si la phase de collecte des données est étalée sur une longue période, il devient impossible de dater précisément la mesure de la fécondité. D’autre part, le calcul des taux de fécondité est complexe du fait de la nécessité de se référer à la date de l’enquête, tout en travaillant par groupes d’âges quinquennaux et par période triennale d’observation.
Nous décrivons ici une démarche plus simple qui consiste à produire des estimations de la fécondité par année d’âge et par année de calendrier. Ces estimations peuvent très facilement être agrégées pour fournir des estimations pour des groupes d’âge plus larges et pour des périodes pluriannuelles.
Comme pour la méthode EDS, les traitements initiaux doivent être réalisés sur les données individuelles. Il est donc généralement raisonnable d’estimer la fécondité directement à partir des histoires génésiques en utilisant la fonction de durée de vie intégrée dans un programme d’analyse statistique comme Stata. Une routine utile pour effectuer ces calculs dans Stata a été publiée par Schoumaker (2013). Les calculs sont toutefois suffisamment faciles pour qu’on puisse les mener à partir de simples tableaux croisés des données. Nous expliquons ici comment procéder.
Données nécessaires et hypothèses
Données nécessaires
Deux séries de données sont nécessaires, toutes deux produites couramment lors du traitement d’une enquête ayant recueilli des histoires génésiques détaillées. La première est une série dont l’unité d’analyse est la femme – c’est-à-dire qu’il y a un enregistrement par femme. Ces données sont nécessaires pour estimer le dénominateur des taux de fécondité. La seconde série de données a l’enfant comme unité d’analyse – c’est-à-dire qu’il y a un enregistrement par enfant – mais des informations de base sur la mère (essentiellement sa date de naissance) sont aussi incluses dans chaque enregistrement.
Pour estimer la fécondité, les informations suivantes doivent figurer dans les données.
a) Série des femmes
- Le mois et l’année de naissance de chaque femme, éventuellement en appliquant la procédure CMC (century-month code) de numérotation des mois à partir du début du siècle des EDS.
- Le mois et l’année de l’interview.
- Toutes les variables nécessaires pour ajuster les données en tenant compte du plan d’échantillonnage et des pondérations.
- Les variables importantes en fonction desquelles on souhaite établir des différentiels de fécondité, en sachant que les variables à la date de l’enquête ne s’appliquaient peut-être pas au moment où ont eu lieu les événements d’intérêt (les naissances récentes).
b) Série des enfants
- La date de naissance de l’enfant – mois et année – éventuellement convertie en code CMC.
- La date de naissance de la mère – mois et année – éventuellement convertie en code CMC.
- Toutes les variables nécessaires pour ajuster les données en tenant compte du plan d’échantillonnage et des pondérations.
- Les mêmes covariables en fonction desquelles établir des différentiels de fécondité.
Précautions et mises en garde
- Les taux de fécondité par année d’âge calculés à partir d’enquêtes de taille relativement modeste fournissent des indications sur la qualité des données, mais ils sont presque toujours trop erratiques pour être utilisés directement. Leur agrégation en groupes quinquennaux (ainsi, éventuellement, qu’un lissage des taux au moyen d’un modèle relationnel de Gompertz) est presque toujours nécessaire.
- De la même façon, les taux par année de calendrier tirés des données d’enquête peuvent ne pas être fiables. Les données de plusieurs années doivent être combinées pour produire une estimation plus fiable. Dans l’idéal, on doit cependant éviter de regrouper plus de trois années pour éviter d’aplatir les tendances de la fécondité.
- Les taux estimés peuvent être affectés par l’omission et la mauvaise datation des naissances déclarées.
- Les taux estimés ne seront pas les mêmes que ceux produits par la méthode EDS. D’une part, l’estimation de la période d’exposition au risque est légèrement différente (la méthode EDS utilise des mois complets, nous des demi-mois). D’autre part, il y a aussi une différence sur la période de référence des taux qui peut aller jusqu’à 11 mois. On peut cependant calculer les taux pour des années allant de juillet à juin (et donc centrées sur le 1er janvier, ou en fait pour toute période de 12 mois) en manipulant convenablement le numérateur et le dénominateur.
Application de la méthode
Nous définissons les termes suivants :
- le mois de naissance de l'enfant
- l'année de naissance de l'enfant
- le mois de naissance de la mère
- l'année de naissance de la mère
- le mois où la mère est interviewée
- l'année où la mère est interviewée
- le nombre total de naissances des mères âgées de x à la naissance de leur enfant l’année t
- les personnes-années d’exposition au risque des femmes âgées de x l’année t.
Les taux sont calculés selon les étapes suivantes. Pour éviter de devoir faire des hypothèses sur l’exposition au risque au cours du mois de l’interview, nous laissons de côté l’exposition au risque et les naissances survenant au cours de ce mois.
Nous présentons le cas général où toutes les femmes ne sont pas interviewées la même année civile. Le processus peut être simplifié lorsque toutes les femmes sont interviewées la même année.
Etape 1 : Etablir un tableau des naissances de chaque année par âge de la mère à la naissance de l’enfant
Cette étape produit le numérateur des taux de fécondité : les naissances des enfants par année civile et par âge de la mère à la naissance.
En principe, l’élaboration de ce tableau est relativement simple, mais des précautions doivent être prises pour déterminer correctement l’âge de la mère à la naissance de son enfant, lorsque mère et enfant ont le même mois de naissance. Si, comme c’est généralement le cas, le jour de naissance n’est pas connu, on doit décider aléatoirement que le jour de naissance de la mère tombe avant ou après le jour de naissance de l’enfant. Ceci peut être fait en créant une variable binaire, b, et en utilisant un générateur de nombres aléatoires, mais cette procédure a des conséquences sur la cohérence et la réplicabilité de la recherche. A la place, b peut être généré à partir d’une variable supposément uniforme qui n’a pas de rapport avec notre objet, par exemple le jour du mois où la mère a été interviewée. Nous définissons donc b= 1 si le jour de l’interview est supérieur à 15 et b= 0 si le jour du mois est le 15 ou moins.
L’âge (révolu) de la mère à la naissance d’un enfant donné, x, est donné par
où int() représente la partie entière du terme entre parenthèses.
Extraire un tableau faisant apparaître le nombre total de naissances , dans chaque cellule définie par les combinaisons de et x, en pondérant les données si nécessaire et en s’assurant d’exclure les naissances survenues dans le mois où la mère a été interviewée.
Etape 2 : Calculer l’âge de chaque femme au début de l’année où elle a été interviewée
Travaillant sur la série de données des femmes (c’est-à-dire un enregistrement par femme), on commence par calculer l’âge des femmes au 1er janvier de l’année de l’interview, xI, en supposant que les naissances des mères sont distribuées uniformément le long de chaque mois) :
(1)
Il s’ensuit que l’âge de la mère au 1er janvier de toute autre année, t, (t ≤ YI) est égal à
xI – (YI - t).
Etape 3 : Calculer l’exposition au risque de chaque femme dans l’année de son interview
Au cours de l’année où elle est interviewée, une femme n’est exposée au risque d’une naissance qu’une fraction du temps (c’est-à-dire, la partie de l’année qui précède l’interview). Dans ce cas, le calcul de l’exposition au risque est fonction du fait qu’elle a été interviewée avant ou après l’anniversaire fêté cette année-là. Si son mois de naissance précède le mois de l’interview, elle sera exposée au risque d’avoir une naissance à l’âge xI pendant
d'année, et pendant
d'année à l’âge xI+1. Si son mois de naissance est le même que, ou postérieur à, celui de l’interview, son exposition au risque d’une naissance l’année de l’interview sera de
d’année à l’âge xI et de
année à l’âge xI+1.
Notez qu’au cours de la dernière année civile complète, l’exposition agrégée par femme est de 1 an, alors qu’elle est de (MI - 1)/12 d’année, l’année de l’interview, quelle que soit la position relative du mois de la naissance et du mois de l’interview.
Les variables donnant l’exposition de chaque femme aux âges xI et xI + 1 au cours de l’année de l’interview doivent être calculées puis agrégées (et pondérées si nécessaire), afin de donner un tableau d’exposition agrégée par âge l’année de l’interview.
Etape 4a : Calculer l’exposition au risque de chaque femme au cours de la dernière année complète avant l’interview.
Au cours de la dernière année civile complète précédant son interview, l’année t=YI - 1, une femme est âgée de xI - 1 avant son anniversaire, et xI par la suite. Avec la même hypothèse de répartition uniforme des naissances au long de l’année, la fraction d’année entre le 1er janvier et l’anniversaire de la femme est égale à
Le restant de l'année, la femme est âgée de xI et l'exposition est égale à
Sur la base de ces deux formules, les variables donnant les expositions de chaque femme aux âges xI et xI+1 l’année YI - 1 doivent être calculées puis agrégées (après pondération si nécessaire) afin de produire un tableau de l’exposition agrégée par âge cette année.
Etape 4b : Calculer l’exposition au risque pour les années complètes antérieures
Les histoires génésiques sont recueillies rétrospectivement auprès de l’ensemble des femmes, chacun d’entre elles fournissant des informations sur toute la période où elle a été exposée au risque de fécondité. Certaines peuvent avoir déménagé ou changé de caractéristiques sur d’autres points au cours de la période, mais comme des histoires résidentielles et économiques sont rarement recueillies dans les enquêtes de fécondité, il est généralement impossible d’en tenir compte dans le calcul des taux de fécondité. L’interprétation de certains résultats comme la fécondité par lieu de résidence peut en conséquence manquer de clarté.
En revanche, comme les dates de naissance sont fixées une fois pour toutes et que la population féminine étudiée reste constante au fil du temps, l’exposition agrégée des femmes atteignant l’âge x une année où l’exposition de toutes les femmes est complète, v, sera aussi égale à l’exposition de la cohorte les années antérieures, c’est-à-dire
(2)
Etape 5 : Calculer les taux de fécondité par âge
Pour calculer l’exposition totale à chaque âge chaque année, E(x,t), on cumule les résultats obtenus aux étapes 3 et 4 pour chaque âge et pour chaque année (complète et incomplète). Si le travail de terrain s’est déroulé sur deux années civiles, YI - 1 se réfère à deux années différentes, tout comme YI. L’exposition totale pour la dernière année civile où elle peut être calculée ne couvre que l’exposition partielle des femmes interviewées la seconde année du travail de terrain, alors que l’exposition totale de l’année immédiatement antérieure couvre l’exposition partielle des femmes interviewées la première année du travail de terrain et la pleine exposition au cours de cette année des femmes interviewées la seconde année du travail de terrain.
Les taux de fécondité à l’âge x l’année t sont égaux à
Les taux de fécondité par groupe quinquennal d’âge conventionnel sont obtenus en cumulant les naissances des femmes au sein de chaque groupe d’âge, et en divisant par le cumul des expositions dans ce groupe d’âge. Ainsi si i=(x/5)-2 pour x = 15, 20, …, 45, on a
et
Pour combiner les données de plusieurs années, on doit cumuler les numérateurs et les dénominateurs séparément avant d’en faire le rapport pour obtenir le taux :
Exemple
Nous utilisons les données de l’EDS du Malawi en 2004. Le travail de terrain a été réalisé entre octobre 2004 et février 2005.
Etape 1 : Etablir un tableau des naissances de chaque année par âge de la mère à la naissance de l’enfant
Après allocation aléatoire de l’âge de la mère à la naissance de son enfant dans les cas où l’une et l’autre ont le même mois de naissance, le tableau croisé de l’année de naissance des enfants par âge de la mère à la naissance de son enfant est tel qu’il apparait au tableau 1. On constate qu’il y a eu un important décalage ou une forte omission des naissances en 2001 et 2002, puisque le nombre de naissances déclaré pour ces années est inférieur d’environ 20 % à celui déclaré en 2003. Les naissances déclarées en 2004 sont moins nombreuses qu’en 2003 en partie parce que des femmes n’ont pas été exposées pendant toute l’année civile, et parce que les naissances survenues le mois de l’interview ont été exclues de l’analyse.
Tableau 1 Naissances classées par âge de la mère à la naissance depuis 2001, Malawi, EDS 2004
Âge | Année de naissance | ||||
|---|---|---|---|---|---|
2001 | 2002 | 2003 | 2004 | 2005 | |
13 | 1,11 | 0,96 | 0,00 | 0,00 | 0,00 |
14 | 6,44 | 3,26 | 2,00 | 4,02 | 0,00 |
15 | 19,70 | 12,74 | 17,21 | 14,65 | 0,00 |
16 | 49,84 | 41,40 | 49,87 | 39,00 | 0,00 |
17 | 93,45 | 88,79 | 93,36 | 61,67 | 0,00 |
18 | 113,79 | 133,70 | 153,38 | 110,40 | 0,00 |
19 | 145,63 | 148,18 | 162,51 | 162,48 | 0,00 |
20 | 146,03 | 166,63 | 177,72 | 155,24 | 0,00 |
21 | 159,60 | 137,76 | 179,68 | 174,46 | 0,00 |
22 | 137,50 | 128,60 | 147,12 | 148,44 | 0,00 |
23 | 115,15 | 110,30 | 173,94 | 138,36 | 2,12 |
24 | 109,24 | 96,07 | 144,74 | 149,19 | 0,00 |
25 | 113,58 | 93,61 | 105,37 | 117,68 | 0,00 |
26 | 82,08 | 69,68 | 107,11 | 105,36 | 0,00 |
27 | 74,37 | 77,16 | 129,50 | 105,48 | 0,00 |
28 | 66,31 | 66,14 | 73,87 | 91,96 | 0,00 |
29 | 62,92 | 63,28 | 75,42 | 80,13 | 0,00 |
30 | 55,93 | 55,44 | 76,98 | 68,16 | 0,00 |
31 | 55,89 | 42,38 | 59,05 | 56,76 | 0,00 |
32 | 55,11 | 72,47 | 59,85 | 61,36 | 0,00 |
33 | 34,74 | 54,08 | 72,14 | 41,23 | 0,00 |
34 | 28,09 | 44,41 | 67,04 | 52,00 | 0,00 |
35 | 50,00 | 25,28 | 41,26 | 48,16 | 0,00 |
36 | 41,61 | 33,88 | 27,42 | 33,56 | 0,00 |
37 | 30,57 | 25,46 | 48,50 | 30,46 | 0,00 |
38 | 24,47 | 32,07 | 31,55 | 36,85 | 0,00 |
39 | 23,05 | 16,87 | 39,64 | 22,38 | 0,00 |
40 | 16,95 | 20,66 | 12,56 | 26,47 | 0,00 |
41 | 19,67 | 9,72 | 17,17 | 9,87 | 0,00 |
42 | 12,44 | 7,72 | 9,79 | 8,89 | 0,00 |
43 | 9,43 | 10,35 | 17,32 | 9,15 | 0,00 |
44 | 4,17 | 10,98 | 7,11 | 11,11 | 0,00 |
45 | 4,94 | 4,86 | 3,63 | 4,29 | 0,00 |
46 | 4,02 | 9,07 | 14,65 | 4,96 | 0,00 |
47 | 0,00 | 0,82 | 3,96 | 2,35 | 0,00 |
48 | 0,00 | 0,00 | 2,16 | 0,00 | 0,00 |
49 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 |
TOTAL | 1967,84 | 1914,75 | 2404,58 | 2186,55 | 2,12 |
Etape 2 : Calculer l’âge de chaque femme au début de l’année où elle a été interviewée
L’âge des femmes au début de l’année où elles ont été interviewées est calculé d’après l’équation 1. Le tableau 2 donne une illustration du calcul. A la troisième ligne (cas 444 3), la femme est née en août 1984 et a été interviewée en octobre 2004. Au 1er janvier 2004 elle était âgée de 19 ans (colonne 4). A la neuvième (avant-dernière) ligne (cas 528 2), la femme née en janvier 1970 et interviewée en janvier 2005 était âgée de 34 ans au 1er janvier 2005.
Tableau 2 Données illustrant le calcul de l’exposition au risque, Malawi, EDS 2004
Cas n° | Date de | Date d’interview | Âge au début de l’année d’interview | Exposition l’année de l’interview |
| Exposition dans la dernière année complète | ||
|---|---|---|---|---|---|---|---|---|
Âge inférieur | Âge supérieur | Âge inférieur | Âge supérieur | |||||
(1) | (2) | (3) | (4) | (5) | (6) |
| (7) | (8) |
| 443 4 | Février 1976 | Octobre 2004 | 27 | 0,125 | 0,625 |
| 0,125 | 0,875 |
| 443 10 | Octobre 1974 | Octobre 2004 | 29 | 0,750 | 0,000 |
| 0,792 | 0,208 |
| 444 3 | Août 1984 | Octobre 2004 | 19 | 0,625 | 0,125 |
| 0,625 | 0,375 |
| 445 2 | Juin 1983 | Octobre 2004 | 20 | 0,458 | 0,292 |
| 0,458 | 0,542 |
| 519 7 | Mai 1989 | Janvier 2005 | 15 | 0,000 | 0,000 |
| 0,375 | 0,625 |
| 522 2 | Mars 1979 | Janvier 2005 | 25 | 0,000 | 0,000 |
| 0,208 | 0,792 |
| 526 4 | Décembre 1989 | Janvier 2005 | 15 | 0,000 | 0,000 |
| 0,958 | 0,042 |
| 526 7 | Septembre 1979 | Janvier 2005 | 25 | 0,000 | 0,000 |
| 0,708 | 0,292 |
| 528 2 | Janvier 1970 | Janvier 2005 | 34 | 0,000 | 0,000 |
| 0,042 | 0,958 |
| 529 2 | Octobre 1972 | Janvier 2005 | 32 | 0,000 | 0,000 |
| 0,792 | 0,208 |
Etape 3 : Calculer l’exposition au risque de chaque femme dans l’année de son interview
Les colonnes (5) et (6) du tableau 2 illustrent le calcul de l’exposition au risque de chaque femme l’année de l’interview. A la première ligne (cas 443 4) la femme a eu son 28ème anniversaire en février 2004. Sous l’hypothèse que les jours de naissance sont, en moyenne, au milieu de chaque mois, elle a passé 0,125 an (1,5/12) âgée de 27 ans en 2004, et 0,625 an (7,5 mois de mi-février à la fin septembre, le mois précédant son interview) âgée de 28 ans la même année.
La femme de la deuxième ligne (cas 443 10) a son anniversaire le mois où elle a été enquêtée. Elle a donc eu 9 mois pleins d’exposition (0,75 an) à 29 ans en 2004, et pas d’exposition par la suite.
Les femmes interviewées en janvier 2005 n’ont pas eu d’exposition l’année de leur interview, puisque nous ne prenons pas en compte l’exposition (et les naissances) au cours de ce mois.
Etape 4a : Calculer l’exposition au risque de chaque femme au cours de la dernière année complète avant l’interview
Les colonnes (7) et (8) du tableau 2 illustrent le calcul de l’exposition au risque lors de la dernière année complète où les femmes ont été exposées au risque d’une naissance dans les données de l’enquête. Pour les femmes interviewées en 2004, c’est en 2003. Pour les femmes interviewées en 2005, c’est en 2004.
Dans le deuxième cas (443 10), l’exposition en 2003 – dernière année complète d’exposition – est de 9,5 mois à 28 ans et 2,5 mois à 29 ans. Comme exprimé par l’équation 2, l’année précédente, l’exposition aurait été distribuée dans les mêmes proportions entre les âges diminués d’un an : en 2002, l’exposition est de 9,5 mois à 27 ans et 2,5 mois à 28 ans.
Dans le dernier cas présenté (529 2), la femme a passé à peu près 9,5 mois (0,792 an) à 31 ans en 2004 et 2,5 mois (0,208 an) à 32 ans en 2004.
En additionnant les expositions par année d’âge et année civile calculées à l’étape 4 on obtient l’exposition au risque du tableau 3.
Tableau 3 Exposition agrégée par année d’âge et année civile, Malawi, EDS 2004
Âge | 2002 | 2003 | 2004 | 2005 |
|---|---|---|---|---|
11 | 0,063 | 0,000 | 0,000 | 0,000 |
12 | 198,291 | 0,063 | 0,000 | 0,000 |
13 | 468,833 | 198,291 | 0,063 | 0,000 |
14 | 432,083 | 468,833 | 197,506 | 0,000 |
15 | 490,890 | 432,083 | 409,831 | 0,049 |
16 | 522,245 | 490,890 | 370,078 | 0,402 |
17 | 597,259 | 522,245 | 431,191 | 0,216 |
18 | 606,502 | 597,259 | 444,050 | 0,337 |
19 | 594,975 | 606,502 | 528,989 | 0,622 |
20 | 573,166 | 594,975 | 514,654 | 0,674 |
21 | 480,330 | 573,166 | 521,777 | 0,354 |
22 | 574,521 | 480,330 | 489,303 | 1,172 |
23 | 486,871 | 574,521 | 422,082 | 0,166 |
24 | 405,933 | 486,871 | 503,468 | 0,939 |
25 | 405,592 | 405,933 | 416,489 | 0,729 |
26 | 407,569 | 405,592 | 350,520 | 0,000 |
27 | 346,264 | 407,569 | 354,229 | 0,425 |
28 | 313,426 | 346,264 | 349,949 | 0,265 |
29 | 286,749 | 313,426 | 300,703 | 0,337 |
30 | 308,209 | 286,749 | 262,300 | 0,177 |
31 | 252,422 | 308,209 | 252,010 | 0,000 |
32 | 309,337 | 252,422 | 256,686 | 0,166 |
33 | 267,239 | 309,337 | 217,728 | 0,000 |
34 | 183,176 | 267,239 | 271,954 | 0,000 |
35 | 185,172 | 183,176 | 226,209 | 0,868 |
36 | 222,879 | 185,172 | 151,012 | 0,000 |
37 | 217,592 | 222,879 | 166,838 | 0,000 |
38 | 236,389 | 217,592 | 192,603 | 0,110 |
39 | 177,195 | 236,389 | 194,856 | 0,363 |
40 | 161,461 | 177,195 | 195,769 | 0,591 |
41 | 142,134 | 161,461 | 155,461 | 0,000 |
42 | 173,338 | 142,134 | 133,356 | 0,166 |
43 | 168,616 | 173,338 | 126,403 | 0,000 |
44 | 148,788 | 168,616 | 147,170 | 0,088 |
45 | 140,768 | 148,788 | 143,087 | 0,088 |
46 | 138,297 | 140,768 | 125,995 | 0,000 |
47 | 72,711 | 138,297 | 124,497 | 0,000 |
48 | 0,606 | 72,711 | 117,910 | 1,027 |
49 | 0,000 | 0,606 | 53,140 | 0,000 |
TOTAL | 1169,89 | 11697,89 | 1011,87 | 10,330 |
Etape 5 : Calculer les taux de fécondité par âge
Les taux de fécondité par année d’âge pour chaque année civile sont obtenus en divisant les naissances du tableau 1 par les populations exposées au risque du tableau 3. Les résultats figurent au tableau 4.
Tableau 4 Taux de fécondité par année d’âge et année civile, Malawi, EDS 2004
Âge | 2001 | 2002 | 2003 | 2004 |
|---|---|---|---|---|
11 | 0,000 | 0,000 | 0.000 | 0,000 |
12 | 0,000 | 0,000 | 0.000 | 0,000 |
13 | 0,003 | 0,002 | 0,000 | 0,000 |
14 | 0,013 | 0,008 | 0,004 | 0,020 |
15 | 0,038 | 0,026 | 0,040 | 0,036 |
16 | 0,083 | 0,079 | 0,102 | 0,105 |
17 | 0,154 | 0,149 | 0,179 | 0,143 |
18 | 0,191 | 0,220 | 0,257 | 0,249 |
19 | 0,254 | 0,249 | 0,268 | 0,307 |
20 | 0,304 | 0,291 | 0,299 | 0,302 |
21 | 0,278 | 0,287 | 0,313 | 0,334 |
22 | 0,282 | 0,224 | 0,306 | 0,303 |
23 | 0,284 | 0,227 | 0,303 | 0,328 |
24 | 0,269 | 0,237 | 0,297 | 0,296 |
25 | 0,279 | 0,231 | 0,260 | 0,283 |
26 | 0,237 | 0,171 | 0,264 | 0,301 |
27 | 0,237 | 0,223 | 0,318 | 0,298 |
28 | 0,231 | 0,211 | 0,213 | 0,263 |
29 | 0,204 | 0,221 | 0,241 | 0,266 |
30 | 0,222 | 0,180 | 0,268 | 0,260 |
31 | 0,181 | 0,168 | 0,192 | 0,225 |
32 | 0,206 | 0,234 | 0,237 | 0,239 |
33 | 0,190 | 0,202 | 0,233 | 0,189 |
34 | 0,152 | 0,242 | 0,251 | 0,191 |
35 | 0,224 | 0,137 | 0,225 | 0,213 |
36 | 0,191 | 0,152 | 0,148 | 0,222 |
37 | 0,129 | 0,117 | 0,218 | 0,183 |
38 | 0,138 | 0,136 | 0,145 | 0,191 |
39 | 0,143 | 0,095 | 0,168 | 0,115 |
40 | 0,119 | 0,128 | 0,071 | 0,135 |
41 | 0,114 | 0,068 | 0,106 | 0,064 |
42 | 0,074 | 0,045 | 0,069 | 0,067 |
43 | 0,063 | 0,061 | 0,100 | 0,072 |
44 | 0,030 | 0,074 | 0,042 | 0,075 |
45 | 0,036 | 0,035 | 0,024 | 0,030 |
46 | 0,055 | 0,066 | 0,104 | 0,039 |
47 | 0,000 | 0,011 | 0,029 | 0,019 |
48 | 0,000 | 0,000 | 0,030 | 0,000 |
49 | 0,000 | 0,000 | 0,000 | 0,000 |
Indice synthétique | 5,61 | 5,20 | 6,32 | 6,36 |
Les résultats varient fortement d’une année à l’autre, les estimations de l’indice synthétique de fécondité différant de plus d’un enfant par femme entre 2002 et 2003. L’estimation de l’indice synthétique en 2004, bien que calculée sur une exposition partielle cette année-là pour la plupart des femmes, est très cohérente avec l’estimation de 2003. La forme de la distribution par âge (cf. figure 1) est très cohérente entre les trois années, bien qu’elle soit établie à partir de taux par année d’âge. Ceux-ci font cependant preuve d’une grande variabilité, même après avoir regroupé les trois années de 2002 à 2004.
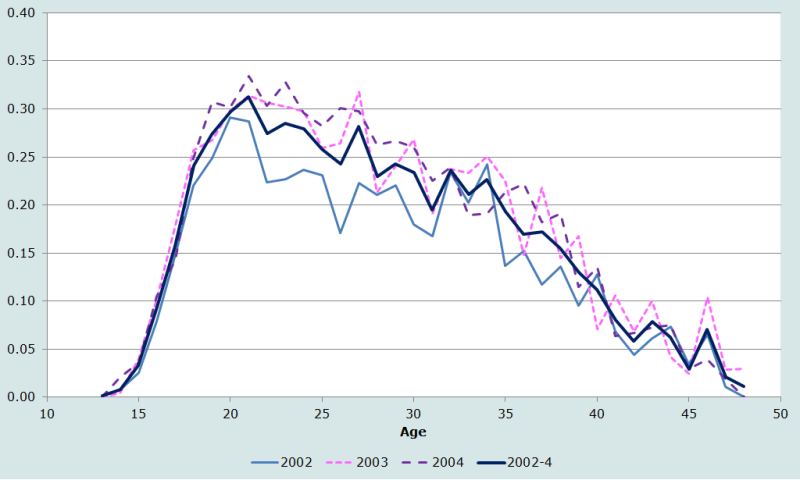
Le regroupement par classe d’âge quinquennale donne les résultats du tableau 5.
Tableau 5 Taux de fécondité par groupe d’années d’âge et année civile, Malawi EDS 2004
Group d’âge | 2002 | 2003 | 2004 | 2002-4 | DHS* |
|---|---|---|---|---|---|
15-19 | 0,151 | 0,180 | 0,178 | 0,169 | 0,162 |
20-24 | 0,254 | 0,304 | 0,312 | 0,290 | 0,293 |
25-29 | 0,210 | 0,261 | 0,283 | 0,252 | 0,254 |
30-34 | 0,204 | 0,235 | 0,222 | 0,221 | 0,222 |
35-39 | 0,129 | 0,180 | 0,184 | 0,164 | 0,163 |
40-44 | 0,075 | 0,078 | 0,086 | 0,080 | 0,080 |
45-49 | 0,042 | 0,049 | 0,021 | 0,036 | 0,035 |
Indice synthétique | 5,32 | 6,44 | 6,43 | 6,05 | 6,05 |
* Les taux pour la période de trois années ayant précédé l’EDS de 2004. | |||||
Source : Measure DHS StatCompiler | |||||
Les différences entre les deux dernières colonnes entre les taux de fécondité par âge obtenus ici et ceux figurant dans l'enquête EDS sont minimes. Toutefois, les taux de fécondité beaucoup plus faibles pour 2002 (et 2001, qui ne figurent pas ici) méritent qu’on prête attention à de possibles erreurs concernant les périodes de référence ainsi qu’à des reports de naissances.
Références
Cleland J. 1996. "Demographic data collection in less developed countries", Population Studies 50(3):433-450. doi: https://dx.doi.org/10.1080/0032472031000149556
Rutstein S and G Rojas. 2003. Guide to DHS Statistics. Calverton, MD: ORC Macro.
Schoumaker B. 2010. "Reconstructing fertility trends in sub-Saharan Africa by combining multiple surveys affected by data quality problems " Paper presented at Population Association of America 2010 Annual Meeting. Dallas, TX, April 15-17, 2010.
Schoumaker B. 2011. "Omissions of births in DHS birth histories in sub-Saharan Africa: Measurement and determinants " Paper presented at Population Association of America 2011 Annual Meeting. Washington D.C., March 31 - April 2, 2011.
Schoumaker B. 2013. “A Stata module for computing fertility rates and TFRs from birth histories: tfr2”, Demographic Research 28(Article 38):1093–1144. doi: https://doi.org/10.4054/DemRes.2013.28.38
- Printer-friendly version
- Log in to post comments
