Estimation indirecte de la mortalité des jeunes enfants
Description de la méthode
Les méthodes indirectes, dont Brass et Coale (1968) ont été les pionniers, consistent à estimer la mortalité des jeunes enfants à partir des informations sur les nombres agrégés d’enfants nés vivants et d’enfants encore en vie (ou décédés) déclarés par des femmes classées par groupe d’âge (ou par durée depuis la première naissance ou par durée de mariage). Cette information est intitulée histoire génésique résumée des naissances (en anglais, summary birth history, SBH). La quantité de détails varie : de seulement deux questions (nombre d’enfants déjà nés et nombre d’enfants encore vivants) à une histoire détaillée posant des questions sur les garçons et les filles séparément et sur les enfants survivants vivant avec leur mère ou vivant ailleurs, comme on l’a vu dans l’introduction à l’analyse de la mortalité des jeunes enfants, en présentant la suite des questions dans l’histoire génésique complète des EDS. Parmi les enfants nés de femmes classées par âge (ou par durée depuis la première naissance, ou par durée de mariage) la proportion de ceux qui sont décédés reflète le niveau de la mortalité des jeunes enfants, mais elle est affectée aussi par d’autres éléments, en particulier la répartition des âges à la maternité et le schéma par âge de la mortalité des jeunes enfants. Les jeunes mères ont généralement de jeunes enfants, qui ont été exposés au risque de décéder peu de temps et à des périodes récentes ; pour ces mères, la proportion d’enfants décédés reflète donc les risque de mortalité à un âge précoce. Au contraire, les mères plus âgées, ont un mélange d’enfants jeunes et d’autres plus âgés exposés au risque de décéder plus longtemps et dans un passé en moyenne plus ancien. Par le jeu de modèles de fécondité et de mortalité des jeunes enfants, les proportions d’enfants décédés sont converties en probabilités de décéder avant des âges exacts de l’enfance, nq0. Plus les femmes sont âgées, plus la valeur de n est élevée.
Si la mortalité a évolué au fil du temps, les probabilités estimées reflètent les taux de mortalité qui ont prévalu à divers âges et diverses dates. Heureusement, une méthode de « localisation dans le temps » a été développée, qui permet d’estimer à quelle période antérieure s’appliquent les probabilités de décès du moment qui ont été approximées à partir de la proportion d’enfants décédés. La longueur de ces périodes s’accroit avec l’âge des répondantes. Ainsi, si les probabilités de décéder estimées à partir des déclarations des femmes de différents groupes d’âge sont traduites en un indice de mortalité commun, ces statistiques se réfèrent à différentes dates et permettent de tracer à grand trait l’évolution de la mortalité au fil du temps.
Données nécessaires et hypothèses
Tableaux des données nécessaires
- Nombre de femmes par groupe quinquennal d’âge, de durée de mariage ou de durée depuis la première naissance.
- Nombre d’enfants nés vivants des femmes par groupe quinquennal pertinent (âge, durée depuis la première naissance, durée de mariage).
- Nombre d’enfants nés vivants qui sont décédés (ou encore en vie) au moment de l’enquête, par groupe quinquennal pertinent.
- Nombre de naissances au cours de l’année précédant l’enquête, par groupe quinquennal d’âge (facultatif)
Hypothèses importantes
- Les schémas par âge de la fécondité et de la mortalité des jeunes enfants dans la population sont adéquatement représentés par ceux utilisés dans le modèle lors du développement de la méthode.
- Dans aucune période, la mortalité des enfants ne varie par groupe quinquennal d’âge des mères.
- Il n’y a pas de corrélation entre les risques de mortalité des enfants et la survie des mères (par mortalité ou migration) dans la population (voir les effets du VIH sur les méthodes d’estimation de la mortalité des jeunes enfants).
- Tous les changements récents dans la mortalité des enfants ont été graduels et sont allés dans la même direction.
- Les nombres moyens d’enfants nés vivant par âge (ou par durée de mariage ou durée depuis la première naissance) à un moment donné reflètent bien les schémas de fécondité dans les cohortes correspondantes.
Travaux préparatoires et recherches préliminaires
L’évaluation de la qualité des données pour une histoire génésique résumée des naissances relève d’un sous-ensemble des analyses décrites dans la section sur l’estimation directe de la mortalité des jeunes enfants pour l’analyse d’une histoire génésique complète. Comme une histoire génésique résumée ne contient pas d’information sur les dates de chaque naissance, l’évaluation se limite à l’analyse des agrégats, tabulés par groupe d’âge de la mère (ou durée de mariage ou durée depuis la première naissance, si une telle information est disponible) ; les tabulations par année d’âge peuvent aussi être révélatrices s’il y a une importante attraction sur certains âges.
Comme toujours, les évaluations s’appuient sur la vraisemblance interne des données d’une part et sur la cohérence externe avec d’autres ensembles de données relatives à la population, d’autre part.
Au titre des évaluations internes, un premier contrôle doit porter sur le nombre moyen d’enfants nés vivants dans chaque groupe de femmes. (Notez que le dénominateur approprié pour ces calculs est l’ensemble des femmes, pas le nombre de mères ou le nombre de femmes déjà mariées). A moins que la fécondité ne connaisse une tendance à la hausse, le nombre moyen d’enfants nés vivants (appelé aussi descendance atteinte) doit s’accroitre au fil des groupes quinquennaux d’âge. Un second contrôle doit porter sur le nombre moyen d’enfants décédés pour chaque groupe quinquennal. A moins que la mortalité des jeunes enfants ou la fécondité ne connaissent une tendance à la hausse, le nombre moyen d’enfants décédés doit aussi s’accroitre avec l’âge. Si on dispose de l’information sur le sexe des enfants nés vivants, les rapports de masculinité des naissances doivent être calculés. Comme pour les histoires génésiques complètes, toute tendance pour ces rapports à s’écarter de 100 à 106 garçons pour 100 filles, ou à s’accroitre avec l’âge (ou la durée du mariage ou la durée depuis la première naissance) doit être considérée comme un signal d’alarme, à moins que la population soit connue pour sa pratique d’un avortement sélectif par sexe.
Parmi les contrôles externes, les comparaisons par cohorte des nombres moyens d’enfants nés vivants et d’enfants décédés sont souvent révélatrices ; elles sont décrites pour les histoires génésiques complètes dans la section sur l’estimation directe de la mortalité des jeunes enfants.
Précautions et mises en garde
- La correction des erreurs de données doit être menée avec attention. Les femmes avec des données manquantes sur les nombres d’enfants nés vivants, ou les nombres d’enfants décédés (ou survivants), ou les deux, doivent être exclues de l’analyse. Mais les femmes sans enfants doivent être incluses.
- Les imputations doivent également être faites avec prudence. Dans les grandes enquêtes, l’information sur le nombre d’enfants nés vivant manque le plus souvent chez des femmes sans enfants (voir la correction d’el-Badry, bien qu’il est à noter ici que la correction n’est pas nécessaire car elle affecterait chaque parité moyenne dans la même proportion). La méthode d’imputation « hot deck », où la donnée manquante est remplacée par la valeur observée pour un répondant choisi au hasard, peut entrainer de sérieux biais.
- L’hypothèse selon laquelle la mortalité des enfants ne varie pas en fonction du groupe quinquennal des mères est généralement incorrecte quand la variable temporelle est l’âge. Les enfants de jeunes mères font systématiquement face à une mortalité supérieure à celle des enfants nés de mères âgées de plus de 25 ans. En conséquence, les estimations indirectes tirées des femmes âgées de 15-19 ans (tout particulièrement) et 20-24 ans (dans une certaine mesure) tendent à surestimer la mortalité des jeunes enfants dans la population. Des corrections pour ces effets sont rarement faites (Collumbien and Sloggett 2001). C’est en partie cette distorsion qui a conduit au développement de méthodes fondées sur la durée de mariage ou la durée depuis la première naissance. Mais ces variantes ont-elles-mêmes leurs inconvénients, que nous évoquerons plus loin.
- L’application de la méthode dans des populations où le VIH est très répandu nécessite des précautions (voir la section sur les effets du VIH sur les méthodes d’estimation de la mortalité des jeunes enfants).
Application de la méthode
Histoire génésique résumée des naissances par groupe quinquennal d’âge/durée depuis la première naissance/durée de mariage
Etape 1 : Calculer les proportions de décédés parmi les enfants déjà nés, 5PDx
Pour chaque groupe quinquennal (x, x + 5) de femmes, les proportions d’enfants décédés sont calculées en divisant le nombre d’enfants décédés par le nombre d’enfants nés vivants.
Etape 2 : Calculer les nombres moyens d’enfants nés vivants des femmes dans chaque groupe quinquennal, 5Px
Pour chaque groupe quinquennal de femmes, diviser le nombre déclaré d’enfants nés vivants 5CEBx (CEB pour children ever born) par le nombre de femmes 5Nx dans le groupe. Noter que si la variable de temps est l’âge, le dénominateur doit être l’ensemble des femmes, quels que soient leur état matrimonial ou leur histoire féconde.
Etape 3 : Choisir une famille de tables-types de mortalité
La répartition par âge de la mortalité des jeunes enfants a une grande importance quand il s’agit de traduire une proportion d’enfants décédés en un quotient nq0 classique et de traduire ce quotient nq0 en un indice courant tel que le taux de mortalité avant 5 ans. Dans une population où ont été collectées des histoires génésiques complètes relativement récentes, la famille de tables-types peut être choisie sur cette base en faisant apparaître sur un graphique l’association existante entre 4q1 et 1q0 en même temps que cette même relation dans les tables-types de Coale-Demeny et celles des Nations Unies. Si ce genre de données n’existe pas, on peut choisir la table-type en s’appuyant sur les schémas de mortalité des jeunes enfants observés dans des pays voisins. Il est peu vraisemblable que les données s’ajustent parfaitement à un des modèles. L’analyste doit choisir le modèle qui représente au mieux l’éventail des observations disponibles. La même famille de tables-types doit être utilisée aux étapes 4, 5 et 6. Les étapes 4 et 5 ont différentes variantes, selon que les données qui font l’objet de l’analyse sont classées par âge de la mère (variante a), durée depuis la première naissance de la mère (variante b), ou durée de mariage de la mère (variante c).
Données classées par âge de la mère (variante a)
Etape 4a(1) : Estimer l’âge moyen de la courbe de fécondité par âge
Cette étape n’est nécessaire que lorsque l’analyse s’appuie sur une des tables-types de mortalité des Nations Unies pour les pays en développement. L’âge moyen est calculé à partir des taux de fécondité par âges 5fx de la façon suivante :
Le terme (x + 2) au numérateur représente le point médian du groupe d’âge entre x et x + 5 au moment où ont eu lieu les naissances. Ceci suppose que les taux de fécondité par âge sont calculés à partir d’informations sur les naissances dans l’année précédant l’enquête classées par âge de la femme au moment de l’enquête (voir la section sur l’évaluation de la qualité des données sur la fécondité récente pour plus de détails). Si les taux de fécondité par âge sont calculés à partir des naissances enregistrées par âge de la mère à la naissance, le terme doit être (x + 2,5). Notez que c’est seulement la forme de la courbe de fécondité qui détermine la moyenne ; il n’est donc pas nécessaire de corriger le niveau, par exemple par un modèle relationnel de Gompertz, avant de calculer l’âge moyen.
Etape 4a(2) : Estimer nq0 à partir de chaque 5PDx
Une fois qu’une famille de tables-types de mortalité j a été identifiée, les paramètres appropriés a(x,j), b(x,j) et c(x,j) (et d(x,j) si une table type des Nations Unies est utilisée) sont remplacés dans l’équation suivante :
Notez que d(x, j) est nul, sauf si on utilise les tables-types des Nations Unies.
Tableau 1 Valeurs de a(x,j), b(x,j), c(x,j) et éventuellement d(x,j) pour estimer les probabilités de décéder avant les âges exacts de l’enfance à partir des proportions de décédés parmi les enfants nés vivants, classés par âge de la mère
|
|
Groupe d’âge de la mère et valeur de n dans nq0 |
|||||||
|
Famille j |
Coefficient |
15-19 |
20-24 |
25-29 |
30-34 |
35-39 |
40-44 |
45-49 |
|
Valeur de n dans nq0 |
1 |
2 |
3 |
5 |
10 |
15 |
20 |
|
|
Princeton ‘Nord’ |
a(x,j) |
1,1119 |
1,2390 |
1,1884 |
1,2046 |
1,2586 |
1,2240 |
1,1772 |
|
b(x,j) |
-2,9287 |
-0,6865 |
0,0421 |
0,3037 |
0,4236 |
0,4222 |
0,3486 |
|
|
c(x,j) |
0,8507 |
-0,2745 |
-0,5156 |
-0,5656 |
-0,5898 |
-0,5456 |
-0,4624 |
|
|
Princeton ‘Sud’ |
a(x,j) |
1,0819 |
1,2846 |
1,2223 |
1,1905 |
1,1911 |
1,1564 |
1,1307 |
|
b(x,j) |
-3,0005 |
-0,6181 |
0,0851 |
0,2631 |
0,3152 |
0,3017 |
0,2596 |
|
|
c(x,j) |
0,8689 |
-0,3024 |
-0,4704 |
-0,4487 |
-0,4291 |
-0,3958 |
-0,3538 |
|
|
Princeton ‘Est’ |
a(x,j) |
1,1461 |
1,2231 |
1,1593 |
1,1404 |
1,1540 |
1,1336 |
1,1201 |
|
b(x,j) |
-2,2536 |
-0,4301 |
0,0581 |
0,1991 |
0,2511 |
0,2556 |
0,2362 |
|
|
c(x,j) |
0,6259 |
-0,2245 |
-0,3479 |
-0,3487 |
-0,3506 |
-0,3428 |
-0,3268 |
|
|
Princeton ‘Ouest’ |
a(x,j) |
1,1415 |
1,2563 |
1,1851 |
1,1720 |
1,1865 |
1,1746 |
1,1639 |
|
b(x,j) |
-2,7070 |
-0,5381 |
0,0633 |
0,2341 |
0,3080 |
0,3314 |
0,3190 |
|
|
c(x,j) |
0,7663 |
-0,2637 |
-0,4177 |
-0,4272 |
-0,4452 |
-0,4537 |
-0,4435 |
|
|
Nations Unies ‘Amérique latine’ |
a(x,j) |
0,6892 |
1,3625 |
1,0877 |
0,7500 |
0,5605 |
0,5024 |
0,5326 |
|
b(x,j) |
-1,6937 |
-0,3778 |
0,0197 |
0,0532 |
0,0222 |
0,0028 |
0,0052 |
|
|
c(x,j) |
0,6464 |
-0,2892 |
-0,2986 |
-0,1106 |
0,0170 |
0,0048 |
0,0256 |
|
|
d(x,j) |
0,0106 |
-0,0041 |
0,0024 |
0,0115 |
0,0171 |
0,0180 |
0,0168 |
|
|
Nations Unies ‘Chili’ |
a(x,j) |
0,8274 |
1,3129 |
1,0632 |
0,8236 |
0,6895 |
0,6098 |
0,5615 |
|
b(x,j) |
-1,5854 |
-0,2457 |
0,0196 |
0,0293 |
0,0068 |
-0,0014 |
0,0040 |
|
|
c(x,j) |
0,5949 |
-0,2329 |
-0,1996 |
-0,0684 |
0,0032 |
0,0166 |
0,0073 |
|
|
d(x,j) |
0,0097 |
-0,0031 |
0,0021 |
0,0081 |
0,0119 |
0,0141 |
0,0159 |
|
|
Nations Unies ‘Asie du Sud’ |
a(x,j) |
0,6749 |
1,3716 |
1,0899 |
0,7694 |
0,6156 |
0,6077 |
0,6952 |
|
b(x,j) |
-1,7580 |
-0,3652 |
0,0299 |
0,0548 |
0,0231 |
0,0040 |
0,0018 |
|
|
c(x,j) |
0,6805 |
-0,2966 |
-0,2887 |
-0,0934 |
0,0298 |
0,0573 |
0,0306 |
|
|
d(x,j) |
0,0109 |
-0,0041 |
0,0024 |
0,0108 |
0,0149 |
0,0141 |
0,0109 |
|
|
Nations Unies ‘Extrême orient’ |
a(x,j) |
0,7194 |
1,2671 |
1,0668 |
0,7833 |
0,5765 |
0,4115 |
0,3071 |
|
b(x,j) |
-1,3143 |
-0,2996 |
0,0017 |
0,0307 |
0,0068 |
0,0014 |
0,0111 |
|
|
c(x,j) |
0,5432 |
-0,2105 |
-0,2424 |
-0,1103 |
-0,0202 |
0,0083 |
0,0129 |
|
|
d(x,j) |
0,0093 |
-0,0029 |
0,0019 |
0,0098 |
0,0165 |
0,0213 |
0,0251 |
|
|
Nations Unies ‘Général’ |
a(x,j) |
0,7210 |
1,3115 |
1,0768 |
0,7682 |
0,5769 |
0,4845 |
0,4760 |
|
b(x,j) |
-1,4686 |
-0,3360 |
0,0109 |
0,0439 |
0,0176 |
0,0034 |
0,0071 |
|
|
c(x,j) |
0,5746 |
-0,2475 |
-0,2695 |
-0,1090 |
0,0038 |
0,0036 |
0,0246 |
|
|
d(x,j) |
0,0095 |
-0,0034 |
0,0021 |
0,0105 |
0,0165 |
0,0187 |
0,0189 |
|
|
Sources: Tables de Princeton: Division de la Population des Nations Unies (1984); Tables des Nations Unies: UN Population Division (1991) |
||||||||
Pour chaque groupe d’âge (x, x + 5), nq0 est estimé en multipliant la partie droite de l’équation par la valeur observée de 5PDx.
Etape 5a : Estimer la date de référence t(x) de chaque nq0 estimé
La famille de tables-types de mortalité j ayant été identifiée, les paramètres e(x,j), f(x,j) et g(x,j) sont remplacés dans l’équation suivante :
La localisation des estimations dans le temps est obtenue en retranchant les t(x) de la date du recensement ou de l’enquête (tableau 2).
Tableau 2: Valeurs de e(x,j), f(x,j) et g(x,j) pour estimer la date de référence t(x) pour les probabilités de décéder avant les âges exacts de l’enfance à partir des proportions d’enfants décédés parmi les enfants nés vivants par âge de la mère
|
|
|
Groupe d’âge de la mère et valeur de n dans nq0 |
|
||||||
|
Famille j |
Coefficient |
15-19 |
20-24 |
25-29 |
30-34 |
35-39 |
40-44 |
45-49 |
|
|
Valeur de n dans nq0 |
1 |
2 |
3 |
5 |
10 |
15 |
20 |
|
|
|
Princeton ‘Nord’ |
e(x,j) |
1,0921 |
1,3207 |
1,5996 |
2,0779 |
2,7705 |
4,1520 |
6,9650 |
|
|
f(x,j) |
5,4732 |
5,3751 |
2,6268 |
-1,7908 |
-7,3403 |
-12,2448 |
-13,9160 |
|
|
|
g(x,j) |
-1,9672 |
0,2133 |
4,3701 |
9,4126 |
14,9352 |
19,2349 |
19,9542 |
|
|
|
Princeton ‘Sud’ |
e(x,j) |
1,0900 |
1,3079 |
1,5173 |
1,9399 |
2,6157 |
4,0794 |
7,1796 |
|
|
f(x,j) |
5,4443 |
5,5568 |
2,6755 |
-2,2739 |
-8,4819 |
-13,8308 |
-15,3880 |
|
|
|
g(x,j) |
-1,9721 |
0,2021 |
4,7471 |
10,3876 |
16,5153 |
21,1866 |
21,7892 |
|
|
|
Princeton ‘Est’ |
e(x,j) |
1,0959 |
1,2921 |
1,5021 |
1,9347 |
2,6197 |
4,1317 |
7,3657 |
|
|
f(x,j) |
5,5864 |
5,5897 |
2,4692 |
-2,6419 |
-8,9693 |
-14,3550 |
-15,8083 |
|
|
|
g(x,j) |
-1,9949 |
0,3631 |
5,0927 |
10,8533 |
17,0981 |
21,8247 |
22,3005 |
|
|
|
Princeton ‘Ouest’ |
e(x,j) |
1,0970 |
1,3062 |
1,5305 |
1,9991 |
2,7632 |
4,3468 |
7,5242 |
|
|
f(x,j) |
5,5628 |
5,5677 |
2,5528 |
-2,4261 |
-8,4065 |
-13,2436 |
-14,2013 |
|
|
|
g(x,j) |
-1,9956 |
0,2962 |
4,8962 |
10,4282 |
16,1787 |
20,1990 |
20,0162 |
|
|
|
Nations Unies ‘Amérique latine’ |
e(x,j) |
1,1703 |
1,6955 |
1,8296 |
2,1783 |
2,8836 |
4,4580 |
6,9351 |
|
|
f(x,j) |
0,5129 |
4,1320 |
2,9020 |
-2,5688 |
-10,3282 |
-17,1809 |
-19,3871 |
|
|
|
g(x,j) |
-0,3850 |
-0,1635 |
3,4707 |
9,0883 |
15,4301 |
20,4296 |
23,4007 |
|
|
|
Nations Unies ‘Chili’ |
e(x,j) |
1,3092 |
1,6897 |
1,8368 |
2,2036 |
2,9955 |
4,7734 |
7,4495 |
|
|
f(x,j) |
1,9474 |
4,6176 |
2,6370 |
-3,3520 |
-11,4013 |
-17,8850 |
-19,0513 |
|
|
|
g(x,j) |
-0,7982 |
-0,0173 |
4,0305 |
9,9233 |
16,3441 |
20,8883 |
23,0529 |
|
|
|
Nations Unies ‘Asie du Sud’ |
e(x,j) |
1,1922 |
1,7173 |
1,8631 |
2,1808 |
2,7654 |
4,1378 |
6,4885 |
|
|
f(x,j) |
0,7940 |
4,3117 |
2,8767 |
-2,7219 |
-10,8808 |
-18,6219 |
-22,2001 |
|
|
|
g(x,j) |
-0,5425 |
-0,1653 |
3,5848 |
9,3705 |
16,2255 |
22,2390 |
26,4911 |
|
|
|
Nations Unies ‘Extrême orient’ |
e(x,j) |
1,2779 |
1,7471 |
1,9107 |
2,3172 |
3,2087 |
5,1141 |
7,6383 |
|
|
f(x,j) |
1,5714 |
4,2638 |
2,7285 |
-2,6259 |
-9,8891 |
-15,3263 |
-15,5739 |
|
|
|
g(x,j) |
-0,6994 |
-0,0752 |
3,5881 |
9,0238 |
14,7339 |
18,2507 |
19,7669 |
|
|
|
Nations Unies ‘Général’ |
e(x,j) |
1,2136 |
1,7025 |
1,8360 |
2,1882 |
2,9682 |
4,6526 |
7,1425 |
|
|
f(x,j) |
0,9740 |
4,1569 |
2,8632 |
-2,6521 |
-10,3053 |
-16,6920 |
-18,3021 |
|
|
|
g(x,j) |
-0,5247 |
-0,1232 |
3,5220 |
9,1961 |
15,3161 |
19,8534 |
22,4168 |
|
|
|
Sources: Tables de Princeton: Division de la Population des Nations Unies (1984); Tables des Nations Unies: UN Population Division (1991) |
|||||||||
Données classées par durée depuis la première naissance des femmes (variante b)
Etape 4b : Estimer nq0 à partir de chaque 5PDx
Une fois qu’une famille de tables-types de mortalité j a été identifiée, les paramètres appropriés a(x,j), b(x,j) et c(x,j) sont remplacés dans l’équation suivante :
Tableau 3: Valeurs de a(x,j), b(x,j), c(x,j) pour estimer les probabilités de décéder avant les âges exacts de l’enfance à partir des proportions d’enfants décédés parmi les enfants nés vivants classés par durée depuis la première naissance de la mère
|
|
|
Durée depuis la première naissance de la mère |
|||||
|
Famille j |
Coefficient |
0-4 |
5-9 |
10-14 |
15-19 |
20-24 |
|
|
Valeur de n dans nq0 |
2 |
5 |
5 |
5 |
10 |
||
|
Princeton ‘Nord’ |
a(x,j) |
1,1980 |
1,2248 |
1,2076 |
1,2030 |
1,3292 |
|
|
b(x,j) |
-0,1266 |
-0,1919 |
-0,0105 |
0,0896 |
0,1598 |
||
|
c(x,j) |
0,0038 |
-0,0870 |
-0,2911 |
-0,4265 |
-0,5778 |
||
|
Princeton ‘Sud’ |
a(x,j) |
1,1705 |
1,3166 |
1,2952 |
1,2836 |
1,5269 |
|
|
b(x,j) |
-0,1461 |
-0,3157 |
-0,0423 |
0,1308 |
0,2659 |
||
|
c(x,j) |
0,0051 |
-0,0971 |
-0,4295 |
-0,6496 |
-0,9174 |
||
|
Princeton ‘Est’ |
a(x,j) |
1,2182 |
1,2769 |
1,2731 |
1,2585 |
1,3410 |
|
|
b(x,j) |
-0,1809 |
-0,2268 |
0,0005 |
0,1216 |
0,1749 |
||
|
c(x,j) |
0,0214 |
-0,1052 |
-0,3720 |
-0,5013 |
-0,5964 |
||
|
Princeton ‘Ouest’ |
a(x,j) |
1,2049 |
1,2573 |
1,2431 |
1,2469 |
1,4258 |
|
|
b(x,j) |
-0,1553 |
-0,2266 |
-0,0230 |
0,0999 |
0,1948 |
||
|
c(x,j) |
0,0135 |
-0,0944 |
-0,3409 |
-0,5267 |
-0,7454 |
||
Note : les coefficients et les valeurs de n dans nq0 ont été mis à jour par Hill à partir de ceux publiés dans Hill and Figueroa (2001)
Pour chaque groupe d’âge (x, x + 5), nq0 est estimé en multipliant la partie droite de l’équation par la valeur observée de 5PDx (Tableau 3).
Etape 5b : Estimer la date de référence t(x) de chaque nq0 estimé
La famille de tables-types de mortalité j ayant été identifiée, les paramètres e(x,j), f(x,j) et g(x,j) sont remplacés dans l’équation suivante :
Tableau 4: Valeurs de e(x,j), f(x,j) et g(x,j) pour estimer la date de référence t(x) pour les probabilités de décéder avant les âges exacts de l’enfance à partir des proportions d’enfants décédés parmi les enfants nés vivants classés par durée depuis la première naissance de la mère
|
|
|
Durée depuis la première naissance de la mère |
||||
|
Famille j |
Coefficient |
0-4 |
5-9 |
10-14 |
15-19 |
20-24 |
|
Valeur de n dans nq0 |
2 |
5 |
5 |
5 |
10 |
|
|
Princeton ‘Nord’ |
e(x,j) |
1,71 |
2,16 |
0,66 |
-1,96 |
-3,85 |
|
f(x,j) |
1,07 |
4,36 |
3,50 |
-0,90 |
-6,42 |
|
|
g(x,j) |
-0,35 |
0,12 |
6,65 |
17,66 |
28,94 |
|
|
Princeton ‘Sud’ |
e(x,j) |
1,68 |
2,29 |
1,19 |
-1,01 |
-2,68 |
|
f(x,j) |
0,96 |
3,84 |
3,45 |
-0,18 |
-5,06 |
|
|
g(x,j) |
-0,32 |
-0,01 |
5,41 |
15,03 |
25,21 |
|
|
Princeton ‘Est’ |
e(x,j) |
1,68 |
2,19 |
0,71 |
-1,96 |
-4,06 |
|
f(x,j) |
0,99 |
4,28 |
3,63 |
-0,71 |
-6,35 |
|
|
g(x,j) |
-0,33 |
0,02 |
6,36 |
17,42 |
29,14 |
|
|
Princeton ‘Ouest’ |
e(x,j) |
1,70 |
2,20 |
0,86 |
-1,46 |
-2,97 |
|
f(x,j) |
1,03 |
4,20 |
3,47 |
-0,69 |
-5,80 |
|
|
g(x,j) |
-0,34 |
0,06 |
6,21 |
16,49 |
26,65 |
|
Les résultats sont présentés au Tableau 4. Note : les coefficients et les valeurs de n dans nq0 ont été mis à jour par Hill à partir de ceux publiés dans Hill and Figueroa (2001).
Données classées par durée depuis le mariage de la mère (variante c)
Etape 4c : Estimer nq0 à partir de chaque 5PDx
Une fois qu’une famille de tables-types de mortalité j a été identifiée, les paramètres appropriés a(x,j), b(x,j) et c(x,j) sont remplacés dans l’équation suivante :
Tableau 5: Valeurs de a(x,j), b(x,j), c(x,j) pour estimer les probabilités de décéder avant les âges exacts de l’enfance à partir des proportions d’enfants décédés parmi les enfants nés vivants classées par durée de mariage de la mère
|
|
|
Durée de mariage de la mère |
|||||
|
Famille j |
Coefficient |
0-4 |
5-9 |
10-14 |
15-19 |
20-24 |
25-29 |
|
Valeur de n dans nq0 |
2 |
3 |
5 |
10 |
15 |
20 |
|
|
Princeton ‘Nord’ |
a(x,j) |
1,2615 |
1,1957 |
1,3067 |
1,4701 |
1,5039 |
1,4798 |
|
b(x,j) |
-0,5340 |
-0,4103 |
-0,0103 |
0,1763 |
0,0039 |
-0,2487 |
|
|
c(x,j) |
0,1252 |
-0,0930 |
-0,4618 |
-0,7268 |
-0,7071 |
-0,5582 |
|
|
Princeton ‘Sud’ |
a(x,j) |
1,3103 |
1,2309 |
1,2774 |
1,3493 |
1,3592 |
1,3532 |
|
b(x,j) |
-0,5856 |
-0,3463 |
0,0336 |
0,1366 |
-0,0315 |
-0,1978 |
|
|
c(x,j) |
0,1367 |
-0,1073 |
-0,3987 |
-0,5403 |
-0,4944 |
-0,4099 |
|
|
Princeton ‘Est’ |
a(x,j) |
1,2299 |
1,1611 |
1,2036 |
1,2773 |
1,3014 |
1,3160 |
|
b(x,j) |
-0,3998 |
-0,2451 |
0,0171 |
0,1015 |
-0,0219 |
-0,1630 |
|
|
c(x,j) |
0,0910 |
-0,0797 |
-0,2992 |
-0,4276 |
-0,4195 |
-0,3751 |
|
|
Princeton ‘Ouest’ |
a(x,j) |
1,2584 |
1,1841 |
1,2446 |
1,3353 |
1,3875 |
1,4227 |
|
b(x,j) |
-0,4683 |
-0,3006 |
0,0131 |
0,1157 |
-0,0193 |
-0,1954 |
|
|
c(x,j) |
0,1080 |
-0,0892 |
-0,3555 |
-0,5245 |
-0,5472 |
-0,5127 |
|
|
|
|
|
|
|
|
|
|
Pour chaque groupe d’âge (x, x + 5), nq0 est estimé en multipliant la partie droite de l’équation par la valeur observée de 5PDx (Tableau 5).
Etape 5c : Estimer la date de référence t(x) de chaque nq0 estimé
La famille de tables-types de mortalité j ayant été identifiée, les paramètres e(x,j), f(x,j) et g(x,j) sont remplacés dans l’équation suivante :
Table 6: Valeurs de e(x,j), f(x,j) et g(x,j) pour estimer la date de référence t(x) pour les probabilités de décéder avant les âges exacts de l’enfance à partir des proportions d’enfants décédés parmi les enfants nés vivants classées par durée de mariage de la mère
|
|
|
Durée de mariage de la mère et valeur de n dans nq0 |
||||
|
Famille j |
|
0-4 |
5-9 |
10-14 |
15-19 |
20-24 |
|
2 |
5 |
5 |
5 |
10 |
||
|
Princeton ‘Nord’ |
a(x,j) |
1,1980 |
1,2248 |
1,2076 |
1,2030 |
1,3292 |
|
b(x,j) |
–0,1266 |
–0,1919 |
–0,0105 |
0,0896 |
0,1598 |
|
|
c(x,j) |
0,0038 |
–0,0870 |
–0,2911 |
–0,4265 |
–0,5778 |
|
|
Princeton ‘Sud’ |
a(x,j) |
1,1705 |
1,3166 |
1,2952 |
1,2836 |
1,5269 |
|
b(x,j) |
–0,1461 |
–0,3157 |
–0,0423 |
0,1308 |
0,2659 |
|
|
c(x,j) |
0,0051 |
–0,0971 |
–0,4295 |
–0,6496 |
–0,9174 |
|
|
Princeton ‘Est’ |
a(x,j) |
1,2182 |
1,2769 |
1,2731 |
1,2585 |
1,3410 |
|
b(x,j) |
–0,1809 |
–0,2268 |
0,0005 |
0,1216 |
0,1749 |
|
|
c(x,j) |
0,0214 |
–0,1052 |
–0,3720 |
–0,5013 |
–0,5964 |
|
|
Princeton ‘Ouest’ |
a(x,j) |
1,2049 |
1,2573 |
1,2431 |
1,2469 |
1,4258 |
|
b(x,j) |
–0,1553 |
–0,2266 |
–0,0230 |
0,0999 |
0,1948 |
|
|
c(x,j) |
0,0135 |
–0,0944 |
–0,3409 |
–0,5267 |
–0,7454 |
|
Etape 6 : Convertir chaque estimation de nq0 en une estimation de 5q0
Dans les applications de l’estimation indirecte de la mortalité des jeunes enfants présentées ici, chacune des probabilités de décéder avant les âges exacts de l’enfance, nq0, est convertie en une valeur de α, le paramètre de niveau d’un système relationnel logit de tables-types de mortalité. Le paramètre α est ensuite utilisé pour estimer la probabilité de décéder entre la naissance et le 5ème anniversaire, 5q0 :
où les estimations de nq0 proviennent de l’Etape 4 et les valeurs de Ys(n) sont des transformations logit de la table de mortalité qui sert de standard. Ainsi, on obtient une série de valeurs de α correspondant aux probabilités de décéder estimées à partir des données des différents groupes d’âge des répondantes. Pour chaque α on a :
Pour appliquer la démarche du système logit relationnel, il est nécessaire de choisir une table de mortalité pour servir de référence. Pour appliquer la procédure indirecte d’estimation, il faut identifier un réseau de tables-types approprié pour les Etapes 4 et 5, et la table de référence doit être tirée de la même famille de tables. Le niveau précis de la mortalité au sein de la famille est moins important que la famille elle-même (la sélection appropriée permettant de supposer que β est égal à 1 dans le système logit relationnelle). C’est pourquoi nous recommandons de choisir comme standard une table de mortalité avec une espérance de vie de 60 ans.
Etape 7 : Identifier et interpréter les résultats
On doit maintenant évaluer la pertinence des estimations de nq0 obtenues pour chaque groupe d’âge, des estimations correspondantes de 5q0, des estimations des localisations dans le temps et de l’évolution de 5q0 au fil du temps. Représentée graphiquement, la série des 5q0 donne une indication sur l’évolution chronologique de la mortalité des jeunes enfants. Si des données proviennent de plusieurs recensements ou enquêtes, diverses estimations de 5q0 peuvent être comparées pour la même période, permettant ainsi une évaluation de la cohérence et de la fiabilité des données.
Exemple
L’exemple s’appuie sur les données relatives aux enfants nés vivants et aux enfants survivants par âge de la mère, tirées du recensement de 2008 au Malawi. La méthode est mise en œuvre dans le fichier Excel associé.
Etape 1 : Calculer les proportions de décédés parmi les enfants nés vivants, 5PDx
Le tableau 7 présente les données de base sur le nombre de femmes, le nombre d’enfants nés vivants et le nombre d’enfants survivants par groupe quinquennal d’âge de la mère tirées du recensement de 2008 du Malawi. La proportion d’enfants décédés parmi les enfants nés vivants, 5PDx, est calculée comme le complément à l’unité du rapport entre le nombre d’enfants survivants (5CSx pour children surviving) et le nombre d’enfants nés vivants (5CEBx) :
Les résultats apparaissent dans la cinquième et sixième colonnes du Tableau 7.
Tableau 7: Enfants nés vivants et enfants survivants, recensement du Malawi 2008
|
Groupe d’âge x,x+4 |
Nombre de femmes |
Enfants |
Enfants survivants |
Nombre moyen d’enfants nés vivants |
Nombre moyen d’enfants survivants |
Proportion décédés, 5PDx |
|
15-19 |
635 927 |
180 178 |
161 541 |
0,2833 |
0,2540 |
0,1034 |
|
20-24 |
678 071 |
1 038 556 |
919 584 |
1,5316 |
1,3562 |
0,1145 |
|
25-29 |
566 350 |
1 613 374 |
1 398 776 |
2,8487 |
2,4698 |
0,1330 |
|
30-34 |
405 602 |
1 697 566 |
1 426 516 |
4,1853 |
3,5170 |
0,1597 |
|
35-39 |
298 004 |
1 553 676 |
1 266 514 |
5,2136 |
4,2500 |
0,1848 |
|
40-44 |
221 274 |
1 335 242 |
1 043 357 |
6,0343 |
4,7152 |
0,2186 |
|
45-49 |
174 875 |
1 128 423 |
851 048 |
6,4527 |
4,8666 |
0,2458 |
Etape 2 : Calculer les nombres moyens d’enfants nés vivants des femmes dans chaque groupe quinquennal, 5Px
Bien que le nombre moyen d’enfants nés vivants des femmes dans chaque groupe quinquennal d’âge, 5Px, ne soit nécessaire que pour les groupes 15-19, 20-24 et 25-29 ans, nous recommandons de calculer ces valeurs pour tous les groupes d’âge afin d’évaluer la qualité de données. La moyenne est calculée simplement en divisant le nombre d’enfants nés vivants par le nombre de femmes dans le groupe d’âge :
Les résultats apparaissent dans la quatrième colonne du tableau 7. Les rapports de descendance(ou ratios de parité) sont ensuite calculés comme suit :
et
Etape 3 : Choisir une famille de tables-types de mortalité
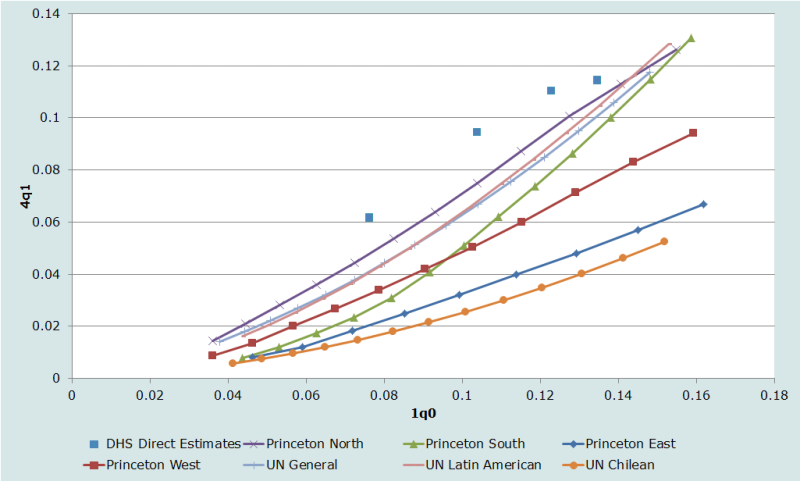
Une série de proportion d’enfants décédés par âge de la mère ne contient pas d’information sur la répartition par âge de la mortalité des jeunes enfants dans une population. Mais dans le cadre de l’analyse de la situation particulière d’un pays, il y aura inévitablement des informations pertinentes pour guider le choix de la table-type à retenir. L’information idéale est la répartition par âge de la mortalité des jeunes enfants tirée d’un histoire génésique complète pour la même population. La comparaison porte sur la relation entre 1q0 et 4q1 et elle fait généralement l’objet d’un graphique, où les points observés sont superposés aux courbes montrant la même relation à différents niveaux de mortalité dans chaque réseau de tables-types.
Plusieurs enquêtes collectant des histoires génésiques complètes ont été réalisées au Malawi. Sur la Figure 1, on a représenté simultanément des estimations directes de la mortalité obtenues pour les 0-4 ans précédant les enquêtes EDS de 1992, 2000 et 2004 (et aussi les 5-9 ans précédant l’enquête de 2000) et des informations tirées des tables-types. (On notera que seuls trois réseaux des Nations Unies sont représentés. Ce choix se justifie parce que la répartition par âge de la mortalité avant 5 ans est très peu différente entre les modèles Général, Asie du Sud et Extrême orient). Toutes les observations font apparaître des rapports entre 4q1 et 1q0 plus élevés que dans tous les réseaux de tables-types. Le meilleur choix dans le cas présent est sans doute le modèle ‘Nord’ de Princeton ; c’est lui que nous utiliserons par la suite.
Etape 4a(1) : Estimer l’âge moyen de la courbe de fécondité par âge
Nous utilisons le réseau ‘Nord’ des tables-types de mortalité de Princeton, mais nous estimons tout de même l’âge moyen à la maternité à partir des taux de fécondité par âge, à des fins d’illustration. Le recensement de 2008 au Malawi incluait une question aux femmes d’âge fécond sur le nombre d’enfants qu’elles avaient eu l’année précédant le recensement. Le Tableau 8 présente les données de base et le calcul de
Tableau 8: Calcul de à partir des données de naissances tirées du recensement de 2008 au Malawi
|
Groupe d’âge x,x+4 |
Nombre de femmes |
Naissances des 12 mois |
Taux de fécondité par âge, 5fx |
Point médian du groupe d’âge (x+2) |
5fx.(x+2) |
|
15-19 |
635 927 |
70 737 |
0,1112 |
17 |
1,891 |
|
20-24 |
678 071 |
169 406 |
0,2498 |
22 |
5,496 |
|
25-29 |
566 350 |
130 331 |
0,2301 |
27 |
6,213 |
|
30-34 |
405 602 |
79 232 |
0,1953 |
32 |
6,251 |
|
35-39 |
298 004 |
43 747 |
0,1468 |
37 |
5,432 |
|
40-44 |
221 274 |
13 956 |
0,0721 |
42 |
3,029 |
|
45-49 |
174 875 |
5 599 |
0,032 |
47 |
1,505 |
|
Total |
|
|
|
|
29,817 |
est ensuite calculé en rapportant le total de la colonne (vi) par le total de la colonne (iv), = 29,817/1,0375 = 28,74.
Etape 4a(2) : Estimer nq0 à partir de chaque 5PDx
Chaque proportion 5PDx est ensuite convertie en un quotient nq0 estimé grâce aux coefficients appropriés tirés du tableau 3, comme il apparait au tableau 9. Ainsi pour le groupe d’âge 35-39 ans on a :
Tableau 9: Estimation du quotient nq0 pour chaque proportion 5PDx.
|
Groupe d’âge |
Proportion d’enfants décédés |
Coefficients de régression pour nq0 (Princeton Modèle ‘Nord’ ) |
nq0 |
|||
|
|
|
a(i) |
b(i) |
c(i) |
|
|
|
15-19 |
0,1034 |
1,1119 |
-2,9287 |
0,8507 |
0,1063 |
|
|
20-24 |
0,1146 |
1,2390 |
-0,6865 |
-0,2745 |
0,1105 |
|
|
25-29 |
0,1330 |
1,1884 |
0,0421 |
-0,5156 |
0,1222 |
|
|
30-34 |
0,1597 |
1,2046 |
0,3037 |
-0,5656 |
0,1528 |
|
|
35-39 |
0,1848 |
1,2586 |
0,4236 |
-0,5898 |
0,1885 |
|
|
40-44 |
0,2186 |
1,2240 |
0,4222 |
-0,5456 |
0,2205 |
|
|
45-49 |
0,2458 |
1,1772 |
0,3486 |
-0,4624 |
0,2441 |
|
Etape 5 : Estimer la date de référence t(x) de chaque quotient nq0 estimé
Pour chaque estimation, la date de référence t(x) avant le recensement ou l’enquête est ensuite obtenue en utilisant les coefficients appropriés tirés du Tableau 4, comme il apparaît au Tableau 10. Ainsi pour le groupe d’âge 30-34 ans, on a :
Le recensement a eu lieu entre le 8 et le 28 juin 2008 ; la date de référence est donc obtenue en retranchant t de 2008,46 (expression décimale du 18 juin 2008). Les résultats apparaissent dans la dernière colonne du Tableau 10.
Tableau 10: Estimation de la date de référence t(x) pour chaque estimation, en années avant le recensement
|
Groupe d’âge |
Coefficients de régression pour la date: Princeton modèle “Nord” |
Date t |
Date de référence |
||
|
e(i) |
f(i) |
g(i) |
(2008,46-t) |
||
|
15-19 |
1,0921 |
5,4732 |
-1,9672 |
1,05 |
2007,42 |
|
20-24 |
1,3207 |
5,3751 |
0,2123 |
2,43 |
2006,03 |
|
25-29 |
1,5996 |
2,6268 |
4,3701 |
4,44 |
2004,03 |
|
30-34 |
2,0779 |
-1,7908 |
9,4126 |
6,81 |
2001,66 |
|
35-39 |
2,7705 |
-7,3403 |
14,9352 |
9,44 |
1999,02 |
|
40-44 |
4,1520 |
-12,2448 |
19,2349 |
12,23 |
1996,24 |
|
45-49 |
6,9650 |
-13,9160 |
19,9542 |
15,12 |
1993,35 |
Etape 6 : Convertir chaque estimation de nq0 en une estimation de 5q0
La dernière étape consiste à convertir chaque quotient nq0 estimé en une estimation de l’indice courant . Ceci permettra de comparer les estimations entre les groupes d’âge. Chaque nq0 est converti en son logit Y(n) au moyen de l’identité Y(n) = 0,5.ln(nq0/(1 – nq0)). La valeur de α est ensuite obtenue en retranchant de Y(n) le logit standard Ys(n), tiré de la table-type de mortalité Nord, sexes réunis, ayant une espérance de vie à la naissance de 60 ans. Chaque α est ensuite utilisé avec le standard Ys(5) de sorte à estimer . Ainsi pour le groupe d’âge 25-29 ans, on a Y(3) = O,5 ln(0,1222/(1-0,1222)) = -0,9857, et α = -0,9857 – (-1,1664) = 0,1806. Donc,
Des estimations de sont tirées de façon analogue en utilisant le logit standard pour 1 an.
Tableau 11: Estimation du paramètre α de la table de mortalité logit pour chaque estimation, et déduction d’une série de et
|
Groupe d’âge |
nq0 |
n |
logit Y(n) |
Standard logit Ys(n) |
α |
||
|
15-19 |
0,1063 |
1 |
-1,0647 |
-1,3300 |
0,2653 |
0,1063 |
0,1612 |
|
20-24 |
0,1105 |
2 |
-1,0431 |
-1,2273 |
0,1842 |
0,0918 |
0,1405 |
|
25-29 |
0,1222 |
3 |
-0,9857 |
-1,1664 |
0,1806 |
0,0912 |
0,1396 |
|
30-34 |
0,1528 |
5 |
-0,8566 |
-1,0900 |
0,2334 |
0,1004 |
0,1528 |
|
35-39 |
0,1885 |
10 |
-0,7299 |
-1,0091 |
0,2791 |
0,1089 |
0,1650 |
|
40-44 |
0,2205 |
15 |
-0,6313 |
-0,9664 |
0,3350 |
0,1203 |
0,1809 |
|
45-49 |
0,2441 |
20 |
-0,5652 |
-0,9138 |
0,3487 |
0,1232 |
0,1850 |
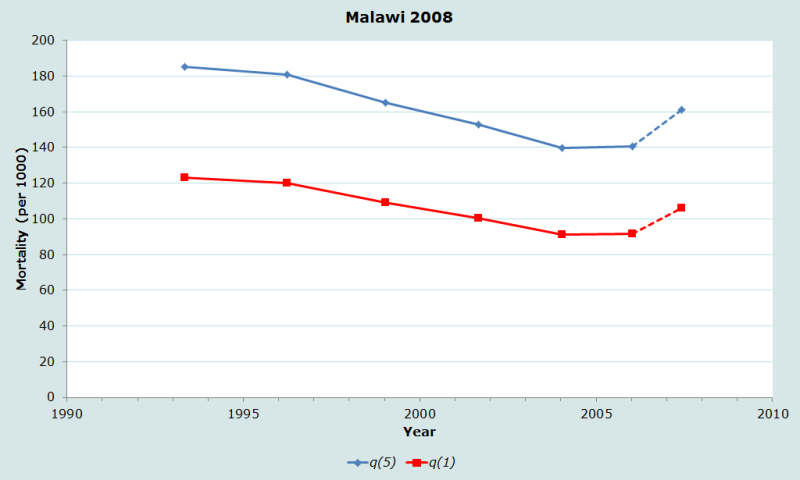
Sur la Figure 2 nous avons représenté chaque estimation et à la date de référence correspondante. Le graphique indique que la mortalité avant 5 ans a baissé, de 185 pour 1000 environ au début des années 1990 à 140 environ en 2005. La légère hausse apparente de la mortalité des jeunes enfants en 2007 ne doit pas être prise en compte, du fait de la surestimation vraisemblable de la mortalité à partir des déclarations des jeunes mères, comme on l’a dit plus haut.
Diagnostics, analyse et interprétation
Contrôles et validation
Indépendamment du mode de collecte des données et de ce qu’on peut savoir sur la formation et la supervision des enquêteurs, un examen méticuleux de la qualité des données est une première étape essentielle de toute analyse. Toutes les séries de données contiennent des erreurs, qui peuvent provenir de plusieurs sources, tels qu’un enquêteur prenant des raccourcis ou une interviewée ne connaissant la réponse correcte à une question, etc.
Un aspect propre à l’histoire génésique résumée doit être souligné pour le contrôle des données : le non-respect de l’hypothèse 2, selon laquelle les risques de mortalité des enfants au cours d’une période ne varient pas avec l’âge de la mère. Dans de nombreuses applications, il apparaît clairement que l’hypothèse ne tient pas. Les risques de décès pour les enfants de mères âgées de 15-19 ans (et l’estimation indirecte de la mortalité des jeunes enfants tirée du nombre d’enfants nés vivants et du nombre d’enfants décédés) sont fréquemment plus élevés, parfois même très nettement, que la moyenne. C’est également vrai dans une moindre mesure pour les enfants des mères de 20-24 ans. Deux facteurs contribuent à ces distorsions : la distribution des enfants par rang de naissance et des facteurs socioéconomiques. Il est bien connu que les premiers nés courent des risques de décéder plus élevés que les naissances de rang plus élevé, et les enfants nés de mères jeunes sont des premiers nés dans une proportion supérieure à la moyenne. Les femmes qui ont des enfants de façon précoce ont également tendance à appartenir à des groupes socioéconomiques moins favorisés et leurs enfants sont ainsi exposés à des risques de mortalité supérieurs à la moyenne. En conséquence, les estimations de mortalité tirées des déclarations des femmes âgées de 15-19 ans doivent être traitées avec beaucoup de circonspection, ou laissées de côté.
Interprétation
Deux caractéristiques essentielles de la méthode doivent être présentes à l’esprit quand on interprète les résultats. D’abord, il n’y a pas d’information sur les dates et les âges dans les données de base. La seule information relative au nombre d’enfants nés vivants d’une femme est que ces naissances sont survenues entre le moment où elle a eu sa première naissance et son âge au moment de l’enquête. Le nombre d’enfants décédés nous en dit encore moins sur l’âge où ces décès ont pu se produire, car l’éventail des âges possibles dépend de la distribution des naissances dans le temps. Il est donc impossible de tirer des conclusions sur les fluctuations à court terme de la mortalité des jeunes enfants à partir d’une histoire génésique résumée. Les déclarations de deux femmes du même âge (ou de la même durée de mariage, ou de la même durée depuis la première naissance) ayant les même nombres d’enfants déjà nés et décédés peuvent refléter des conditions de mortalité différentes. Ce qu’une histoire génésique résumée peut offrir de mieux est une indication générale sur la tendance passée en moyenne. Et même cette tendance moyenne doit être interprétée prudemment pour le passé récent car des biais de sélection affectent les déclarations des femmes âgées de 15-19 ans, et celles âgées de 20-24 ans, quoique dans une moindre mesure.
La seconde caractéristique est que l’information n’est fournie que pour des femmes survivantes résidant encore dans des ménages enquêtés, ce qui risque de représenter un ensemble sélectionné, donc biaisé. La mortalité des enfants nés dans un groupe et dont les mères ne vivent plus dans le groupe ne sera pas incluse dans les mesures. Si ces enfants ont une mortalité plus élevée que ceux nés de mères vivant encore dans le groupe, la mortalité sera sous-estimée. La forme la plus sévère de ce biais peut survenir du fait d’une prévalence élevée du VIH dans le groupe, car en l’absence d’une thérapie rétrovirale largement diffusée, cette prévalence entrainera une forte corrélation positive entre la survie de l’enfant et la survie de la mère (voir la section sur les effets du VIH sur les méthodes d’estimation de la mortalité des jeunes enfants). Mais plus généralement, une certaine corrélation positive entre la survie de la mère et celle de l’enfant est presque systématique dans toute population.
Il peut y avoir d’autres sources de biais de sélection des répondantes. Par exemple, des taux élevés d’immigration impliqueront que des femmes répondent aux questions sur la survie d’enfants nés et élevés ailleurs, alors qu’une forte émigration exclura des réponses sur des enfants qui étaient nés et ont été élevés dans le groupe. Bien qu’il soit impossible de connaître a priori la direction et l’ampleur de tels biais, l’analyste doit avoir leur effet potentiel présent à l’esprit. Les non-réponses sont un problème moins important pour les histoires génésiques résumées que pour les histoires génésiques complètes, car l’information est souvent fournie par des tierces personnes, pas nécessairement par la femme elle-même. Ainsi une histoire génésique résumée peut être établie pour une femme absente du groupe pour un long voyage, alors qu’un histoire génésique complète ne sera pas recueillie si la femme ne peut pas être interviewée en personne.
Description détaillée de la méthode
L’idée que les proportions d’enfants décédés parmi les enfants nés vivants sont des indicateurs de la mortalité des jeunes enfants a une longue histoire. Des questions sur les enfants nés vivants et les enfants survivants étaient déjà intégrées dans le recensement de 1900 aux Etats-Unis (Preston et Haines 1991), le recensement de Grande Bretagne en 1911 et celui du Brésil en 1940, entre autres. Mais la première méthode pour traduire ces proportions en indicateurs d’une table de mortalité classique a été proposée par Brass et Coale (1968).
Pour illustrer l’idée de base, prenez l’exemple simple (et irréaliste) d’une population dans laquelle toutes les femmes ont exactement un enfant, nés quand elles avaient exactement 25 ans, où toutes les femmes survivent de 25 à 30 ans, et où il n’y a pas de migration. Dans une enquête, la proportion d’enfants décédés parmi les enfants nés vivants parmi les femmes âgées de 30 ans exactement mesurerait précisément la probabilité que la cohorte d’enfants décède entre la naissance et le 5ème anniversaire, 5q0. Dans une autre population où toutes les femmes auraient aussi un enfant exactement, mais à 27 ans, la proportion d’enfants décédés mesurerait précisément la probabilité que la cohorte décède avant 3 ans, 3q0.
Ces deux exemples illustrent plusieurs points importants. Premièrement, l’âge des femmes est une approximation de l’exposition au risque de leurs enfants. Toutes choses égales par ailleurs, plus une mère est âgée, plus est longue en moyenne la période d’exposition au risque de décéder de ses enfants. Deuxièmement, l’interprétation d’une proportion d’enfants décédés en termes de mesure classique de la table de mortalité dépend de l’âge à la maternité. Troisièmement, l’équivalence entre une proportion d’enfants décédés et une mesure tirée d’une table de mortalité nécessite une absence d’effets de sélection par la mortalité ou l’émigration, ou d’effets de contamination par l’immigration. Quatrièmement, les mesures obtenues sont relatives à des cohortes (ou des moyennes sur plusieurs cohortes) plutôt qu’à des périodes.
Evidemment dans les populations réelles les enfants naissent de mères de divers âges et sont exposés à des risques de mortalité par âge qui peuvent varier au fil du temps. Les méthodes d’estimation utilisent des schéma-types de fécondité et de mortalité des jeunes enfants par âge pour modéliser les proportions d’enfants décédés parmi les enfants nés vivants, qui peuvent ensuite être rattachées aux paramètres sous-jacents de tables de mortalité. Un trait commun aux données sur la survie des enfants classés par groupe d’âge de la mère est que les proportions d’enfants décédés sont plus élevées pour les femmes âgées de 15-19 et 20-24 ans que pour celles des groupes d’âge suivants, bien qu’elles reflètent des durées moyennes plus courtes d’exposition des enfants. C’est parce que les jeunes femmes qui ont des enfants ont généralement un statut socioéconomique inférieur à la moyenne et que leurs enfants sont, plus souvent que la moyenne, des premiers nés, deux facteurs connus comme exposant les jeunes enfants à des risques de mortalité élevés. La mortalité des enfants nés de ces jeunes mères n’est donc pas représentative de la mortalité de l’ensemble des enfants nés dans cette population. En partie pour éviter ce biais, des méthodes ont été développées où les femmes sont classées par durée de mariage (Sullivan 1972) et durée depuis la première naissance (Hill and Figueroa 2001). Ces méthodes sont aussi moins affectées par les variations de la fécondité.
La méthode a été initialement développée par Brass sans considération explicite des effets des variations de la mortalité sur les estimations, même s’il note qu’en cas de telles variations « les estimations de q(2) et q(3) seraient représentatives de la mortalité moyenne sur une courte période (moins d’une décennie) avant le recensement ou l’enquête » (Brass and Coale, 1968 :116). Il est clair aujourd’hui que la mortalité des jeunes enfants a diminué dans le monde, et très rapidement dans certaines populations. A la suite du travail pionnier de Feeney (1976, 1980), des méthodes ont été développées pour estimer la ‘date de référence’ des estimations tirées de chaque groupe d’âge ou de durée (Coale and Trussell (1977); Palloni and Heligman (1985); Hill and Figueroa (2001)). La proportion d’enfants décédés parmi les enfants nés vivants d’un groupe de femmes représente une moyenne des risques de mortalité sur l’ensemble des cohortes de naissance de ces enfants. Plus les femmes sont âgées, ou plus longue est leur exposition au risque, plus les cohortes d’enfants s’étirent dans le passé et plus s’éloigne dans le temps la période de référence couverte par l’estimation de la mortalité des jeunes enfants tirée de la proportion d’enfants décédés. Comme les risques de mortalité des jeunes enfants sont fortement concentrés sur les très jeunes âges, la date de référence n’est pas très différente en pratique du nombre moyen d’années écoulées depuis la naissance des enfants, si l’évolution de la mortalité a été relativement stable au fil du temps. Les dates de référence exactes pour les estimations de mortalité des jeunes enfants doivent en fait être conçues comme des points centraux du temps avec une distribution des décès autour d’eux. En conséquence, les estimations de mortalité des jeunes enfants tirées des histoires génésiques résumées et les variantes des méthodes indirectes de Brass ne peuvent pas servir à identifier des évolutions ou des crises de la mortalité situées en un point précis du temps. La méthode fournit une bonne description des tendances générales de la mortalité des jeunes enfants, mais lissées par rapport aux fluctuations réelles d’une année sur l’autre qu’on observe dans presque chaque population. D’autres méthodes de mesure (comme les histoires génésiques complètes de naissances) sont nécessaires pour estimer l’impact dans le temps qu’ont pu avoir des interventions visant à améliorer la santé des enfants.
Exposé mathématique (méthodes du Manuel X et des tables-types de mortalité des Nations Unies)
La proportion d’enfants décédés parmi les enfants déjà nés des femmes d’âge exact x, PD(x), est une moyenne des probabilités de décéder des cohortes pondérées par les naissances,
<
où f(y) est le taux de fécondité à l’âge y, x–yqc0 est la probabilité de décéder avant l’âge (x-y) pour la cohorte née (x-y) années plus tôt, et α est l’âge du début de la période féconde. L’expression est identique pour la durée de mariage et la durée depuis la première naissance, à ceci près que α devient 0. Les proportions d’enfants décédés pour des groupes quinquennaux d’âge ou de durée peuvent ensuite être estimées en faisant la moyenne des estimations ponctuelle de PD sur l’ensemble du groupe quinquennal, moyenne pondérée par les distributions supposées de population Nx à chaque x. On suppose le plus souvent que la population sous-jacente peut être considérée comme stable, avec un taux de croissance compatible avec les paramètres démographiques qui sous-tendent les PD(x), et que la table de mortalité aux âges adultes est la même que celle utilisée dans le calcul des PD(x). Ces calculs utilisent des groupes d’âge discrets, soit par exemple, en utilisant des années d’âge,
Des schémas-types de f, q et N sont utilisés pour modéliser les valeurs de 5PDx, qui sont rapportées aux valeurs appropriées de q par une analyse de régression utilisant les rapports de descendance comme variables indépendantes (voir les équations d’estimation plus haut).
Extensions de la méthode
Variantes par durée de mariage et durée depuis la première naissance
Comme on l’a dit plus haut, sans l’illustrer en détail, des variantes de la méthode originale ont été développées, classant les femmes par durée de mariage (Sullivan 1972) et durée depuis la première naissance (Hill et Figueroa 2001). Ces méthodes ont été mises au point pour éviter deux sources potentielles d’erreur dans la méthode fondée sur l’âge : les effets des variations de la fécondité (qui faussent les rapports de descendance) et la surmortalité des enfants nés de jeunes mères.
Ces variantes sont illustrées plus bas, mais ces deux améliorations ont elles-mêmes leurs limites. Premièrement, rares sont les recensements de population recueillant l’information nécessaire pour classer les femmes et leurs enfants par durée de mariage ou par durée depuis la première naissance. Deuxièmement, concernant la durée de mariage, dans de nombreux pays en développement le mariage n’est pas un préalable nécessaire au début de la vie féconde. En outre, les enfants de mères non mariées ont souvent une mortalité supérieure à celle des enfants de mère mariée. Il peut donc aussi y avoir des distorsions dans les résultats de ces variantes. Quand de telles données sont recueillies, comme dans de nombreux pays arabes où les proportions de naissances hors mariage sont faibles, elles permettent d’apprécier de façon intéressante les mérites des différentes démarches.
Certaines enquêtes, comme les MICS (Enquêtes à indicateurs multiples, conduites sous les auspices de l’Unicef) réalisées avant 2010, ont recueilli des histoires génésiques résumées et les informations nécessaires sur la date du mariage et de la première naissance. La question se pose donc de la méthodologie qu’il faut préférer.
Pour répondre, nous avons utilisé les histoires génésiques complètes recueillies lors de l’EDS 1999-2000 au Bangladesh. Les données ont été présentées dans les trois formats et analysées en utilisant le réseau ‘Sud’ des tables-types de mortalité de Princeton. La Figure 3 donne les estimations de 5q0 pour chaque variante. (On notera que dans le cas étudié les données ne font pas apparaître une forte surmortalité quand l’estimation s’appuie sur le groupe d’âge le plus jeune, 15-19 ans).
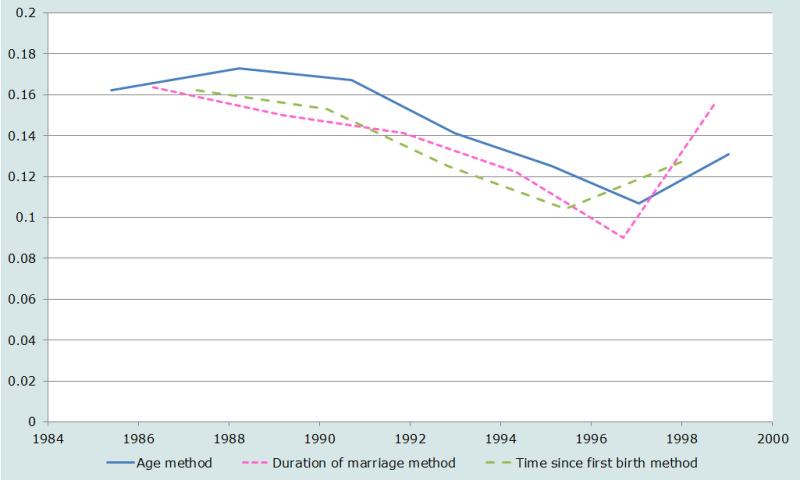
Hormis pour le point le plus récent dans chaque série (soit 15-19 ans pour l’âge et 0-4 ans à la fois pour la durée de mariage et la durée depuis la première naissance), les évolutions générales retracées par les trois estimations sont très semblables. Dans les méthodes par durée de mariage et durée depuis la première naissance, les niveaux sont très proches, mais à partir du groupe d’âge 25-29 ans les estimations par l’âge sont systématiquement les plus élevées, supérieures de 20 pour 1000 en moyenne (à 155 pour 1000) à chacune des deux autres méthodes. Des moyennes simples des estimations pour toutes les durées de mariage ou depuis la première naissance, excepté la plus récente, donnent un résultat presque semblable : 133 pour la durée de mariage et 136 pour la durée depuis la première naissance, bien que les périodes couvertes soient légèrement différentes.
Plusieurs points sont intéressants dans cette application. Premièrement, les méthodes de durée de mariage et durée depuis la première naissance ont été développées en partie pour contourner le problème du biais de sélection dans les points fondés sur l’âge pour les femmes de 15-19 et 20-24 ans. Mais dans la présente application, ces deux méthodes font apparaitre des sauts pour le point le plus récent au moins aussi importants que pour les estimations fondées sur l’âge. Ceci pourrait s’expliquer si le biais a essentiellement pour origine le poids des premiers nés, lesquels sont tous (durée depuis la première naissance) ou presque tous (durée de mariage) concentrés dans la première catégorie, alors qu’ils sont davantage répartis entre les groupes d’âge.
Une seconde question est l’utilisation des rapports de descendance observés au moment de l’enquête pour estimer la répartition dans le temps des naissances passées. Comme on l’a vu plus haut, si la fécondité baisse (même si le calendrier de la fécondité ne se modifie pas), les descendances des jeunes femmes seront relativement basses et celles des femmes âgées seront relativement élevées, ce qui réduira les rapports des descendances au dessous de leur valeur dans les cohortes réelles. La fécondité apparaitra ainsi plus tardive que dans la réalité (et donc la durée d’exposition des jeunes enfants au risque de décéder plus courte), ce qui conduira à surestimer la mortalité des jeunes enfants.
Le Bangladesh ayant connu une forte baisse de la fécondité entre le milieu des années 1980 et l’EDS de 1999-2000, il est intéressant d’essayer d’évaluer l’ampleur du biais. Comme les données proviennent d’une histoire génésique complète, nous pouvons calculer les descendances des cohortes il y a 5 ans, 10 ans, 15 ans, etc., en retranchant les naissances récentes du nombre des enfants nés vivants, et calculer ensuite les rapports de descendances pour des cohortes réelles. Nous utilisons la méthodologie classique (en calculant des rapports P(1)/P(2) et P(2)/P(3)) pour les cohortes qui ont atteint le troisième groupe d’âge ou de durée, c’est-à-dire les groupes d’âge 25-29 ans et plus et les groupes de durée 10-14 ans et plus.
La première partie du tableau 12 compare les rapports de descendance au moment de l’enquête et dans les cohortes. Le résultat est clair et conforme aux attentes pour l’âge, les rapports au moment de l’enquête étant nettement inférieurs aux rapports dans toutes les cohortes, lesquels sont relativement stables de cohorte en cohorte. Mais c’est moins clair pour les méthodes par durée de mariage et durée depuis la première naissance : les rapports P(2)/P(3) sont généralement plus élevés que ceux au moment de l’enquête, alors que les rapports P(1)/P(2) sont tous plus bas.
Tableau 12: Rapports des descendances P(1)/P(2) et P(2)/P(3) calculés au moment de l’enquête et dans les vraies cohortes, Bangladesh, 1999-2000
|
Méthode de l’âge |
||||||
|
Rapport des descendances |
Au moment de l’enquête |
Cohorte âgée de 25-29 |
Cohorte âgée de 30-34 |
Cohorte âgée de 35-39 |
Cohorte âgée de 40-44 |
Cohorte âgée de 45-49 |
|
P(1)/P(2) |
0,269 |
0,342 |
0,311 |
0,327 |
0,361 |
0,336 |
|
P(2)/P(3) |
0,544 |
0,66 |
0,639 |
0,603 |
0,632 |
0,619 |
|
Méthode de la durée de mariage |
||||||
|
Rapport des descendances |
Au moment de l’enquête |
Cohorte 10-14 |
Cohorte 15-19 |
Cohorte 20-24 |
Cohorte 25-29 |
|
|
P(1)/P(2) |
0,353 |
0,352 |
0,288 |
0,274 |
0,287 |
|
|
P(2)/P(3) |
0,635 |
0,682 |
0,65 |
0,598 |
0,603 |
|
|
Méthode de la durée depuis la première naissance |
||||||
|
Rapport des descendances |
Au moment de l’enquête |
Cohorte 10-14 |
Cohorte 15-19 |
Cohorte 20-24 |
|
|
|
P(1)/P(2) |
0,553 |
0,544 |
0,495 |
0,505 |
||
|
P(2)/P(3) |
0,709 |
0,775 |
0,753 |
0,723 |
|
|
Pour apprécier l’importance de cet effet sur les estimations, nous pouvons utiliser les rapports des descendances pour chaque proportion d’enfants décédés parmi les enfants nés vivants (pour les groupes d’âge 25-29 ans et plus et les groupes de durée 10-14 ans et plus). Les trois graphiques de la Figure 4 représentent les estimations originales et celles dans les cohortes localisées à la date de référence, pour les groupes d’âge, les groupes de durée de mariage et les groupes de durée depuis la première naissance respectivement. Le recours aux rapports de descendances dans les cohortes se traduit par des estimations moins élevées aux groupes d’âges 25-29 et 30-34 ans, mais il a peu d’effet sur les estimations obtenues par les deux autres méthodes. C’est sans doute parce que la baisse de la fécondité au Bangladesh pendant cette période était essentiellement due à une hausse de l’âge à la maternité, avec peu d’impact sur la durée du mariage ou la durée depuis la première naissance. Au total, le recours aux rapports de descendance dans les cohortes améliore la cohérence entre méthodes, mais le prix à payer est plutôt élevé : la perte des estimations les plus récentes.
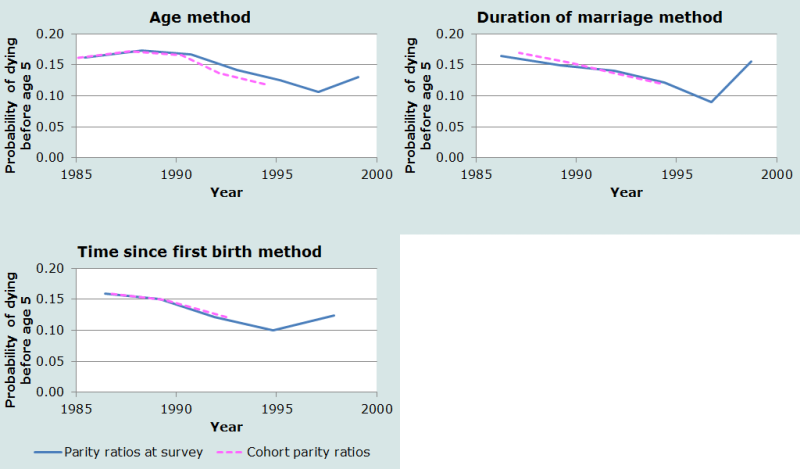
L’idée générale est que la méthode fondée sur l’âge tend à surestimer la mortalité des jeunes enfants si la fécondité évolue rapidement, alors que les effets sur les deux autres méthodes sont faibles. Si les données existent, il est recommandé d’utiliser une des deux autres variantes plutôt que la méthode fondée sur l’âge, mais cela ne vaut sans doute pas la peine d’ajouter une question supplémentaire dans un recensement juste pour obtenir l’information nécessaire.
Autres lectures et références
L’estimation indirecte de la mortalité des jeunes enfants est présentée dans tous les manuels classiques d’estimation indirecte (Sloggett, Brass, Eldridge et al. 1994; Division de la Population des Nations Unies 1984).
Brass W and AJ Coale. 1968. "Methods of analysis and estimation," in Brass, W, AJ Coale, P Demeny, DF Heisel, et al. (eds). The Demography of Tropical Africa. Princeton NJ: Princeton University Press, pp. 88-139.
Brass W, AJ Coale, P Demeny, DF Heisel et al. (eds). 1968. The Demography of Tropical Africa. Princeton NJ: Princeton University Press.
Coale AJ and J Trussell. 1977. "Estimating the time to which Brass estimates apply; Annex I to Preston SH and Palloni A "Fine-tuning Brass-type mortality estimates with data on ages of surviving children", Population Bulletin of the United Nations 10:87-89. https://www.un.org/development/desa/pd/content/population-bulletin-united-nations-special-issue-nos-10
Collumbien M and A Sloggett. 2001. "Adjustment methods for bias in the indirect childhood mortality estimates," in Zaba, B and J Blacker (eds). Brass Tacks: Essays in Medical Demography. London: Athlone, pp. 20-42.
Division de la Population des Nations Unies. 1984. Manuel X. Techniques indirectes d’estimation démographique. New York : Nations Unies, Département des affaires économiques et sociales internationales, ST/ESA/SER.A/81. https://unstats.un.org/unsd/demographic/standmeth/handbooks/Manuel_X-fr.pdf
Feeney G. 1976. "Estimating infant mortality rates from child survivorship data by age of mother", Asian and Pacific Census Newsletter 3(2):12-16. https://hdl.handle.net/10125/3556.
Feeney G. 1980. "Estimating infant mortality trends from child survivorship data", Population Studies 34(1):109-128. doi: https://dx.doi.org/10.1080/00324728.1980.10412839
Hill K and M-E Figueroa. 2001. "Child mortality estimation by time since first birth," in Zaba, B and J Blacker (eds). Brass Tacks: Essays in Medical Demography. London: Athlone, pp. 9-19.
Palloni A and L Heligman. 1985. "Re-estimation of structural parameters to obtain estimates of mortality in developing countries", Population Bulletin of the United Nations 18:10-33. https://www.un.org/development/desa/pd/content/population-bulletin-united-nations-special-issue-nos-18
Preston SH and MR Haines. 1991. Fatal Years: Child Mortality in Late Nineteenth-century America. Princeton, NJ: Princeton University Press.
Sloggett A, W Brass, SM Eldridge, IM Timæus, P Ward and B Zaba. 1994. Estimation of Demographic Parameters from Census Data. Tokyo, Japan: United Nations Statistical Institute for Asia and the Pacific.
Sullivan JM. 1972. "Models for the estimation of the probability of dying between birth and exact ages of early childhood", Population Studies 26(1):79-97. doi: https://dx.doi.org/10.1080/00324728.1972.10405204
UN Population Division. 1991. Child Mortality in Developing Countries. New York: United Nations, Department of Economic and Social Affairs, ST/ESA/SER.A/123. https://www.un.org/development/desa/pd/content/child-mortality-developing-countries-socio-economic-differentials-trends-and-implications
- Printer-friendly version
- Log in to post comments
