La méthode de la balance de l’accroissement démographique de Brass
Description de la méthode
La méthode de la balance de l’accroissement démographique de Brass (growth balance method) est la première de la série des méthodes dites de la répartition des décès pour estimer la complétude de la déclaration des décès relativement à une estimation de la population (Brass 1975). La méthode part de l’observation que dans une population stable (c'est-à-dire une population ayant une structure par âge constante dans le temps, au moins pour les âges adultes, croissant à un taux annuel constant r, fermée aux migrations et avec une bonne déclaration de l’âge), le taux de croissance r est égal au taux de natalité b moins le taux de mortalité d. La même relation est vérifiée dans le groupe d’âge de la population âgée d’au moins x années, c'est-à-dire : où représente le taux auquel la population atteint le groupe d’âge x+ (les personnes âgées d’au moins x années), et est le taux de mortalité dans le même groupe d’âge x+. Si, dans cette population, les décès sont sous-représentés dans la même proportion à chaque âge, alors , où est le taux de mortalité basé sur les décès déclarés dans le groupe d’âge x+, et c est la proportion de décès qui sont déclarés. On peut estimer c à partir de la pente d'une ligne droite ajustée aux points de données [b(x+), d r(x+)]. Cette estimation est en général restreinte aux âges adultes, car la complétude de l’enregistrement des décès d’enfants diffère souvent de celle des décès d’adultes. Les taux de mortalité sont ensuite calculés en divisant le nombre de décès déclarés par c, et en divisant ce nombre par une estimation de la population exposée au risque basée sur la population utilisée pour calculer les taux partiels de natalité et de mortalité avant correction.
Cette méthode est un cas particulier de la méthode plus générale connue sous le nom de ‘méthode généralisée de la balance de l’accroissement démographique’ (generalized growth balance method), qui requiert des estimations de la population à deux instants donnés, mais s’affranchit de l’hypothèse de stabilité de la population. On renvoie le lecteur à la section correspondante pour plus de détails sur la méthode. La version présentée ici figure dans ce manuel comme une méthode que l’on peut considérer lorsqu’on ne dispose que d’un point dans le temps pour les effectifs de population.
Données nécessaires et hypothèses
Tabulation des données nécessaires
- Nombre de décès de femmes (ou hommes) au cours d’une période donnée, répartis par groupe d’âge de 5 ans, et pour le dernier groupe d’âge A+, A étant aussi élevé que possible.
- Nombre de femmes (ou hommes) à un point dans le temps aussi proche que possible de la période considérée, aussi répartis par groupe d’âge de 5 ans, et pour le dernier groupe d’âge A+, A étant aussi élevé que possible.
Hypothèses importantes
- La population est stable, quoique cette hypothèse puisse être relâchée dans certaines limites (voir ci-dessous).
- La complétude de l’enregistrement des décès est la même pour tous les âges au-dessus d’un âge limite inférieure (en général 15 ans).
- La population est fermée aux migrations, quoique cette hypothèse puisse également être relâchée si les migrations nettes sont faibles par rapport aux taux de mortalité, ou si on dispose d’estimations raisonnables de migrants par âge qui peuvent être prises en compte dans l’équation de la balance de l’accroissement démographique (ce qui est un cas très rare en pratique).
Travaux préparatoires et recherches préliminaires
Avant de mettre en œuvre cette méthode, on doit au préalable analyser la qualité des données, et au moins les points suivants:
- structure par âge de la population;
- réparation par sexe de la population;
- structure par âge des décès; et
- réparation par sexe des décès.
Précautions et mises en garde
Lorsqu’ils appliquent cette méthode, les analystes doivent prendre en considération les points suivants :
- Le processus d’interprétation et d’estimation doit prendre en compte la source des données de mortalité (décès déclarés à l’état civil, décès déclarés par les ménages dans les recensements, ou décès déclarés dans les structures sanitaires), comme cela est expliqué plus loin. Cependant, les biais associés à la source des données tendent à avoir moins d’effet sur l’estimation de la complétude avec la méthode de la balance de l’accroissement démographique qu’avec la méthode de l’extinction des cohortes synthétiques.
- Le problème des migrations devient plus sérieux quand on applique la méthode à des zones géographiques régionales, et non plus nationales.
- Il est nécessaire de choisir l’intervalle d’âges sur lequel on ajuste une droite reliant les taux partiels de natalité et de mortalité, et qui permet de calculer la complétude. Les problèmes spécifiques sont : quel est le meilleur âge pour choisir l’intervalle ouvert lorsqu’on suspecte une tendance à l’exagération de l’âge ; comment traiter les points qui se situent au-dessus de la ligne aux âges élevés lorsque la complétude tend à baisser avec l’âge, par exemple dans le cas de migrations associées à la retraite entre les milieux urbain et rural où l’enregistrement est moins complet ; et faut-il exclure les âges en dessous de 30 ou 35 ans, car l’impact des migrations n’y est pas pris en compte spécifiquement.
- Lorsque la complétude des décès déclarés semble être inférieure à 60 %, on conseille de prendre garde aux résultats, car l’incertitude sur les estimations devient importante.
Application de la méthode
Etape 1 : Cumuler la population et les décès à partir du bas
Afin de calculer les taux partiels de natalité et de mortalité, il faut d’abord cumuler les effectifs de population et de décès au cours d’une période de t années, pour tous les âges au-delà de l’âge x. Pour la population, on utilise la formule suivante :
où A est l’âge au début du dernier groupe d’âge ouvert.
On utilise une équation analogue pour calculer le nombre de décès au-delà de l’âge x, notée : D(x+).
Etape 2 : Calcul des personnes-années vécues: PYL(x+)
Pour calculer les taux partiels de natalité et de mortalité, on doit calculer les personnes-années d’exposition au risque de décès. Pour ce faire, on utilise la formule suivante :
où t est la longueur de la période au cours de laquelle les décès ont été enregistrés.
Etape 3 : Calcul du nombre de personnes qui atteignent l’âge x dans la population, N(x)
Le nombre de personnes qui atteignent l’âge x (qui correspond à une arrivée, ou ‘naissance’, dans le groupe d’âge x+) dans la population se calcule comme la moyenne géométrique des effectifs dans les deux groupes quinquennaux adjacents, divisée par 5, et multiplié par t, la longueur de l’intervalle au cours duquel les décès sont déclarés, exprimé en années, selon la formule :
Etape 4: Calcul des taux partiels de natalité et de mortalité, b(x+) et d(x+)
Les taux partiels de natalité et mortalité sont calculés selon les formules suivantes:
et
respectivement.
Etape 5: Représentation graphique, ajustement d’une droite et estimation de la complétude (c)
Pour estimer la complétude de l’enregistrement des décès relativement à la population, on commence par tracer sur un graphique la relation entre b(x+) et d(x+). Les coefficients (pente et ordonnée à l’origine) de la droite de régression orthogonale qui les lient sont calculés selon les formules suivantes :
et
où b est la pente et a l’ordonnée à l’origine de la droite liant les ordonnées yi, c’est à dire les b(x+) et les abscisses xi, c'est-à-dire les d(x+) ; et représentent respectivement les moyennes des deux séries.
Il convient alors d’analyser l’alignement des points et les résidus, de manière à choisir le meilleur intervalle d’âge à garder pour calculer la complétude de l’enregistrement des décès. Ce choix est discuté en détail ci-dessous. En pratique, tout point ayant un résidu supérieur à 1% en valeur absolue devrait être exclu. Une ligne finale est alors tracée à partir des points restants, et on calcule une nouvelle valeur des coefficients a et b pour cette nouvelle ligne.
La complétude de l’enregistrement des décès se calcule alors à partir des valeurs de a et de b selon la formule suivante :
où tc désigne la date du recensement, et tm désigne le milieu de la période au cours de laquelle les décès ont été enregistrés. La justification de cette équation est la suivante : l’inverse de la pente donne une estimation de la complétude de l’enregistrement, en faisant l’hypothèse que le recensement est placé au milieu de la période d’enregistrement des décès. Le second terme est utilisé pour corriger la différence entre la population à la date t et la population en milieu de période tm. En faisant l’hypothèse d’une population stable, croissant à un taux estimé par a, ce ratio se calcule comme suit: .
Etape 6: Estimation des taux de mortalité après correction pour tenir compte de la sous-déclaration des décès
Pour calculer les taux de mortalité au cours de la période d’enregistrement, il faut d’abord estimer la population moyenne, qui, là encore, doit tenir compte de la croissance de la population. On l’obtient en multipliant les effectifs du recensement répartis par groupes d’âge quinquennaux par le coefficient suivant : .
Ensuite, on doit corriger le nombre de décès observés, en les divisant par l’estimation de la complétude c.
Les personnes-années d’exposition sont calculées en multipliant la population moyenne (au temps tm ) par la longueur de la période d’observation t.
Les taux de mortalité, après correction pour tenir compte du fait que l’enregistrement des décès est incomplet, sont alors calculés selon la formule :
Le numérateur et le dénominateur sont tous deux ajustés par le coefficient de croissance de la population : . On pourrait donc ignorer cette correction et obtenir en fin de compte les mêmes chiffres pour les taux de mortalité corrigés. Mais l’estimation de la complétude serait alors équivalente à celle qui s’appliquerait si la population au temps tm était égale à celle observée au temps tc.
Etape 7: Lissage à l’aide d’un système relationnel logit de tables-types de mortalité
Puisque les taux de mortalité par âge peuvent être erratiques, ils doivent être lissés. Ceci peut être réalisé à l’aide d’une fonction relationnelle logit (ajustement de Brass) à partir d’une série de taux de mortalité d’une table type que l’on considère comme ayant le même schéma par âge que la population analysée.
Le classeur Excel associé à ce manuel contient une feuille de calcul qui permet de produire un ensemble de taux de mortalité lissés par un système relationnel logit appliqué à une table-type. L’utilisateur peut choisir une table-type parmi le modèle Général des tables-type des Nations Unies, ou un des quatre modèles régionaux des tables-type de Princeton. On peut aussi choisir comme référence une table de mortalité spéciale, si l’on a une bonne raison de penser que ce schéma par âge correspond mieux au schéma de la mortalité adulte de la population étudiée.
Pour effectuer le lissage, les quotients quinquennaux de mortalité, notés 5qx, sont calculés à partir des taux de mortalité corrigés pour la complétude comme suit :
Puis, on part d’une racine de 1 à cinq ans (l5 = 1), et on calcule de proche en proche les survivants de la table selon la formule : .
Les coefficients α and β s’obtiennent en ajustant le modèle relationnel suivant: où la fonction logit est définie comme:
et où l’exposant s désigne les valeurs de la table-type (le standard). Enfin, on peut établir la table de mortalité lissée en appliquant les coefficients α et β comme suit:
et
Les taux de mortalité lissés se calculent à partir de cette table de mortalité selon les formules :
et
où
soit
et ω représente l’âge ultime de la table de mortalité, au-delà duquel il ne reste plus aucun survivant.
Exemple détaillé
Cet exemple utilise les données du Salvador : les données de la population féminine viennent du recensement de 1961, et les décès féminins de l’état civil pour l’année 1961. Cet exemple apparaît dans la feuille de calcul intitulée : BGB_El Salvador. La date de référence du recensement est la nuit du 5 au 6 mai 1961, c’est cette date qui est entrée comme 1961/05/06 dans la feuille d’introduction.
Etape 1: Cumul de la population, des décès et des migrants à partir du bas
On cumule les effectifs de population et de décès à partir du bas, c'est-à-dire à partir du dernier groupe d’âge (Tableau 1).
Tableau 1 Calcul des effectifs cumulés de population et de décès, El Salvador, Recensement de 1961
Age | 5Nx | 5Dx | N(x+) | D(x+) |
|---|---|---|---|---|
| 0-4 | 214 089 | 6 909 | 1 274 253 | 13 652 |
| 5-9 | 190 234 | 610 | 1 060 164 | 6 743 |
| 10-14 | 149 538 | 214 | 869 930 | 6 133 |
| 15-19 | 125 040 | 266 | 720 392 | 5 919 |
| 20-24 | 113 490 | 291 | 595 352 | 5 653 |
| 25-29 | 91 663 | 271 | 481 862 | 5 362 |
| 30-34 | 77 711 | 315 | 390 199 | 5 091 |
| 35-39 | 72 936 | 349 | 312 488 | 4 776 |
| 40-44 | 56 942 | 338 | 239 552 | 4 427 |
| 45-49 | 46 205 | 357 | 182 610 | 4 089 |
| 50-54 | 38 616 | 385 | 136 405 | 3 732 |
| 55-59 | 26 154 | 387 | 97 789 | 3 347 |
| 60-64 | 29 273 | 647 | 71 635 | 2 960 |
| 65-69 | 14 964 | 449 | 42 362 | 2 313 |
| 70-74 | 11 205 | 504 | 27 398 | 1 864 |
75+ | 16 193 | 1 360 | 16 193 | 1 360 |
Etape 2: Calcul des personnes-années vécues, PYL(x+)
Comme des décès sont enregistrés selon l’année d’âge, les personnes-années vécues dans chaque groupe d’âge (colonne 2 du tableau 2) sont simplement la somme des effectifs à chaque âge dans le recensement (soit la même chose que la colonne 4 du Tableau 1).
Tableau 2 Calcul des personnes-années vécues, du nombre de personnes atteignant l’âge x, des taux partiels de natalité et de mortalité, et des résidus, El Salvador, Recensement de 1961
Age | PYL(x+) | N(x) | b(x+) | d(x+) = X | b(x+) = Y | a+bx | Résidus y-(a+bx) |
|---|---|---|---|---|---|---|---|
| 0-4 | 1 274 253 | 0,00000 | 0,03097 | ||||
| 5-9 | 1 060 164 | 40 362 | 0,03807 | 0,00636 | 0,03807 | 0,03782 | 0,00026 |
| 10-14 | 869 930 | 33 733 | 0,03878 | 0,00705 | 0,03878 | 0,03856 | 0,00022 |
| 15-19 | 720 392 | 27 348 | 0,03796 | 0,00822 | 0,03796 | 0,03981 | -0,00185 |
| 20-24 | 595 352 | 23 825 | 0,04002 | 0,00950 | 0,04002 | 0,04119 | -0,00117 |
| 25-29 | 481 862 | 20 399 | 0,04233 | 0,01113 | 0,04233 | 0,04294 | -0,00061 |
| 30-34 | 390 199 | 16 880 | 0,04326 | 0,01305 | 0,04326 | 0,04501 | -0,00175 |
| 35-39 | 312 488 | 15 057 | 0,04818 | 0,01528 | 0,04818 | 0,04741 | 0,00077 |
| 40-44 | 239 552 | 12 889 | 0,05380 | 0,01848 | 0,05380 | 0,05085 | 0,00295 |
| 45-49 | 182 610 | 10 259 | 0,05618 | 0,02239 | 0,05618 | 0,05506 | 0,00112 |
| 50-54 | 136 405 | 8 448 | 0,06193 | 0,02736 | 0,06193 | 0,06040 | 0,00153 |
| 55-59 | 97 789 | 6 356 | 0,06500 | 0,03423 | 0,06500 | 0,06779 | -0,00279 |
| 60-64 | 71 635 | 5 534 | 0,07725 | 0,04132 | 0,07725 | 0,07542 | 0,00183 |
| 65-69 | 42 362 | 4 186 | 0,09881 | 0,05460 | 0,09881 | 0,08970 | 0,00911 |
| 70-74 | 27 398 | 2 590 | 0,09452 | 0,06803 | 0,09452 | 0,10415 | -0,00963 |
| 75+ | 16 193 |
Etape 3: Calcul des effectifs de personnes atteignant l’âge x dans la population, N(x)
Les effectifs de personnes qui atteignent l’âge x figurent dans la troisième colonne du Tableau 2. Par exemple, le nombre de personnes atteignant l’âge de 70 ans est calculé comme suit :
Etape 4: Calcul des taux partiels de natalité et de mortalité, b(x+) and d(x+)
Les taux partiels de natalité et de mortalité figurent dans la quatrième et la cinquième colonne du Tableau 2. Par exemple, pour l’âge de 20 ans, on a :
et
Etape 5: Représentation graphique, ajustement de la droite de régression, et estimation de la complétude, c
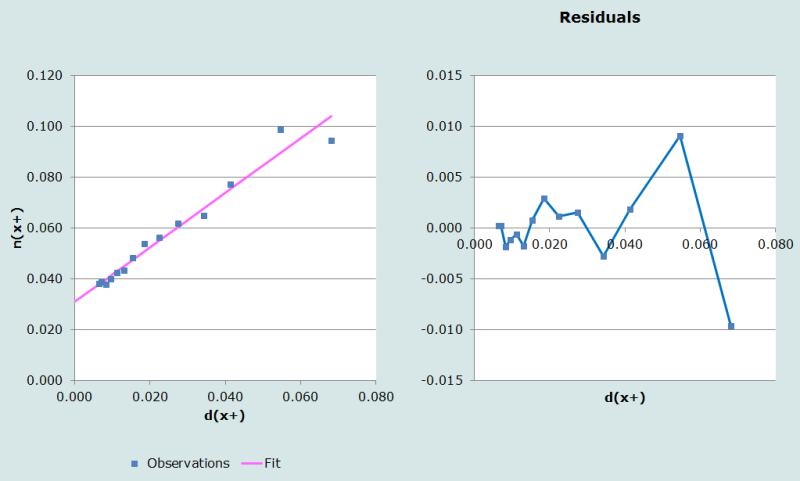
Pour tracer le graphique et ajuster la droite de régression à partir de tous les points représentant les données, on choisit l’âge minimal à 5 ans et l’âge maximal à A–1, où A représente l’âge au début du dernier groupe d’âge, c'est-à-dire l’intervalle ouvert (soit 75 ans dans cet exemple). La Figure 1 présente les points d’ordonnée b(x+) et d’abscisse d(x+). Les coefficients de la droite de régression liant ses points sont calculés selon les formules suivantes :
L’analyse des points figurant sur la Figure 1 suggère que la plupart des points sont approximativement alignés, à l’exception des deux derniers, ceux qui sont situés le plus à droite. On n’observe pas de preuve évidente d’un effet des migrations. Bien que les résidus des deux derniers points tombent juste dans la limite tolérée de moins de 1%, et que nous pouvons donc estimer la complétude de l’enregistrement des décès à 93%, il est utile d’examiner le cas où ces deux points seraient éliminés. Le calcul de la complétude se fait à partir des coefficients a et b, comme suit :
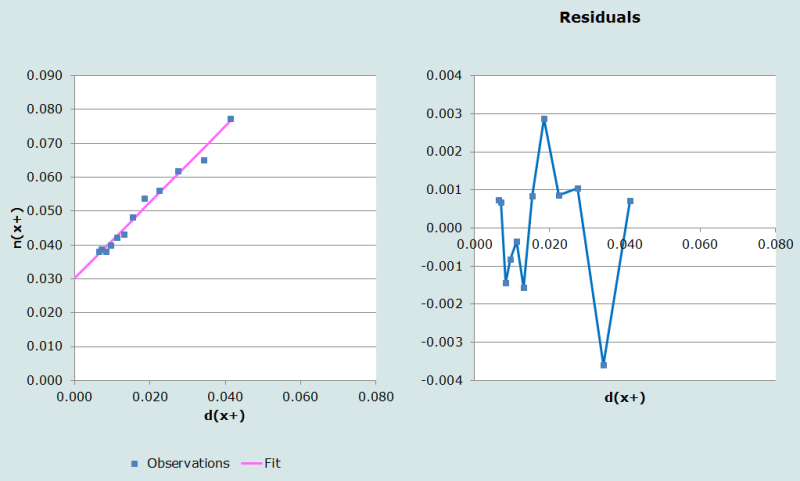
Omettre les deux derniers points, ce qui revient à choisir 64 ans comme la limite supérieure de l’âge, produit un meilleur ajustement, qui apparaît sur la Figure 2, et qui donne une complétude de 89%, ce qui est assez proche de l’estimation précédente, et suggère qu’il n’est pas nécessaire d’omettre ces deux derniers points. Par contre, omettre le dernier point seulement induit un changement notable dans l’estimation, soit une complétude de 82% et un ajustement linéaire moins précis pour certains points situés à gauche, ce qui suggère que cette stratégie n’est pas la meilleure. Pour les populations qui souffrent d’une forte attirance pour les chiffres ronds, une règle générale est de ne pas terminer à un âge qui se termine par zéro.
Etape 6: Calcul des taux de mortalité après correction pour tenir compte de la sous-déclaration des décès
La population au milieu de la période au cours de laquelle les décès sont déclarés est estimée en ajustant la population recensée en tenant compte de la croissance démographique entre les deux dates, soit un taux de 3,1%. Cette estimation apparaît dans la seconde colonne du Tableau 3. Par exemple, pour le groupe d’âge 15-19 ans, l’effectif est calculé de la manière suivante :
Ensuite, les décès sont corrigés pour tenir compte de leur sous-déclaration, en divisant le nombre de décès déclarés dans chaque groupe d’âge par l’estimation de la complétude. Ces calculs apparaissent dans la colonne 3 du Tableau 3. Ainsi, pour le groupe d’âge 15-19 ans, le nombre observé (266 décès figurant en colonne 3 du Tableau 1) est corrigé en 287,5 décès, comme suit :
Les personnes-années vécues apparaissent en colonne 4 du Tableau 3. Ce sont les effectifs de la population au milieu de la période où les décès sont enregistrés (colonne 2 du Tableau 3), multipliés par la durée de la période (en années), qui dans ce cas est simplement 1 an.
Les taux de mortalité, après correction pour tenir compte de la sous-déclaration des décès, figurent en colonne 5 du Tableau 3. Ils sont calculés en divisant le nombre de décès corrigés par les personnes-années vécues dans l’intervalle. Par exemple, pour le groupe d’âge 15-19 ans, le taux de mortalité corrigé se calcule comme suit :
Tableau 3 Calcul des taux de mortalité corrigés, El Salvador, Recensement de 1961
Age | Population ajustée 5Nx(tm) | Décès ajustés 5Dx | Personnes-années ajustées PYL(x,5) | Taux ajustés 5mx |
|---|---|---|---|---|
| 0–4 | ||||
| 5–9 | 191 181 | 659 | 191 181 | 0,0034 |
| 10–14 | 150 282 | 231 | 150 282 | 0,0015 |
| 15–19 | 125 662 | 288 | 125 662 | 0,0023 |
| 20–24 | 114 055 | 315 | 114 055 | 0,0028 |
| 25–29 | 92 119 | 293 | 92 119 | 0,0032 |
| 30–34 | 78 098 | 340 | 78 098 | 0,0044 |
| 35–39 | 73 299 | 377 | 73 299 | 0,0051 |
| 40–44 | 57 225 | 365 | 57 225 | 0,0064 |
| 45–49 | 46 435 | 386 | 46 435 | 0,0083 |
| 50–54 | 38 808 | 416 | 38 808 | 0,0107 |
| 55–59 | 26 284 | 418 | 26 284 | 0,0159 |
| 60–64 | 29 419 | 699 | 29 419 | 0,0238 |
| 65–69 | 15 038 | 485 | 15 038 | 0,0323 |
| 70–74 | 11 261 | 545 | 11 261 | 0,0484 |
75+ | 16 274 | 1 470 | 16 274 | 0,0903 |
Etape 7: Lissage utilisant un système relationnel logit de tables-types de mortalité
Les estimations des quotients quinquennaux de mortalité féminine, notés 5qx, calculés ci-dessus à partir des taux de mortalité corrigés, apparaissent dans la deuxième colonne du Tableau 4. Par exemple, la probabilité pour une femme de 15 ans de décéder avant d’atteindre le 20ème anniversaire, se calcule comme suit :
Les survivants de la table de mortalité se calculent de proche en proche dans les groupes d’âge quinquennaux. Ils apparaissent dans la colonne 3 du Tableau 4. Par exemple, la proportion de personnes survivantes à l’âge de 20 ans se calcule comme suit :
Tableau 4 Calcul des taux de mortalité lissés par le biais d’un système relationnel logit de tables-types de mortalité, El Salvador, Recensement de 1961
| Age | 5qx | lx/l5 | Y(x) obs. | Table-type Princeton Ouest ls(x) | Logit Ys(x) | Ajusté Y(x) | Ajusté l(x) | T(x) | Valeurs lissées 5mx |
|---|---|---|---|---|---|---|---|---|---|
| 0 | |||||||||
| 5 | 0,0171 | 1 | 1,0000 | 1 | 61,957 | 0,0025 | |||
| 10 | 0,0077 | 0,9829 | -2,0258 | 0,9890 | -2,2506 | -2,1978 | 0,9878 | 56,987 | 0,0018 |
| 15 | 0,0114 | 0,9754 | -1,8394 | 0,9805 | -1,9585 | -1,9153 | 0,9788 | 52,071 | 0,0027 |
| 20 | 0,0137 | 0,9643 | -1,6477 | 0,9681 | -1,7060 | -1,6710 | 0,9658 | 47,209 | 0,0035 |
| 25 | 0,0158 | 0,9511 | -1,4836 | 0,9519 | -1,4928 | -1,4649 | 0,9493 | 42,421 | 0,0039 |
| 30 | 0,0216 | 0,9361 | -1,3419 | 0,9337 | -1,3226 | -1,3003 | 0,9309 | 37,721 | 0,0045 |
| 35 | 0,0254 | 0,9159 | -1,1938 | 0,9132 | -1,1766 | -1,1590 | 0,9104 | 33,118 | 0,0051 |
| 40 | 0,0314 | 0,8926 | -1,0588 | 0,8899 | -1,0447 | -1,0314 | 0,8872 | 28,624 | 0,0061 |
| 45 | 0,0407 | 0,8646 | -0,9269 | 0,8628 | -0,9194 | -0,9103 | 0,8606 | 24,254 | 0,0076 |
| 50 | 0,0522 | 0,8294 | -0,7906 | 0,8299 | -0,7925 | -0,7875 | 0,8285 | 20,031 | 0,0105 |
| 55 | 0,0765 | 0,7861 | -0,6507 | 0,7863 | -0,6514 | -0,6511 | 0,7862 | 15,994 | 0,0146 |
| 60 | 0,1122 | 0,7259 | -0,4870 | 0,7289 | -0,4946 | -0,4995 | 0,7308 | 12,202 | 0,0222 |
| 65 | 0,1493 | 0,6445 | -0,2974 | 0,6490 | -0,3074 | -0,3184 | 0,6540 | 8,740 | 0,0339 |
| 70 | 0,2158 | 0,5482 | -0,0968 | 0,5427 | -0,0856 | -0,1039 | 0,5517 | 5,725 | 0,0545 |
| 75 | #N/A | 0,4299 | 0,1411 | 0,4062 | 0,1898 | 0,1625 | 0,4194 | 3,297 | 0,0871 |
| 80 | #N/A | #N/A | #N/A | 0,2545 | 0,5373 | 0,4986 | 0,2695 | 1,575 | 0,1370 |
85 | #N/A | #N/A | #N/A | 0,1201 | 0,9956 | 0,9419 | 0,1320 | 0,571 | 0,2084 |
La transformation logit des proportions de survivants apparait dans la colonne 4 du Tableau 4. Par exemple, le logit de l20 se calcule comme suit:
La transformation logit de la table de mortalité féminine tirée du modèle Ouest des tables-types de Princeton avec une espérance de vie e°= 60 ans (colonne 5 du Tableau 4) apparait dans la colonne 6 du même tableau. Comme on peut le voir sur la Figure 3, le modèle Ouest semble bien ajuster les données, sauf peut-être pour les âges jeunes.
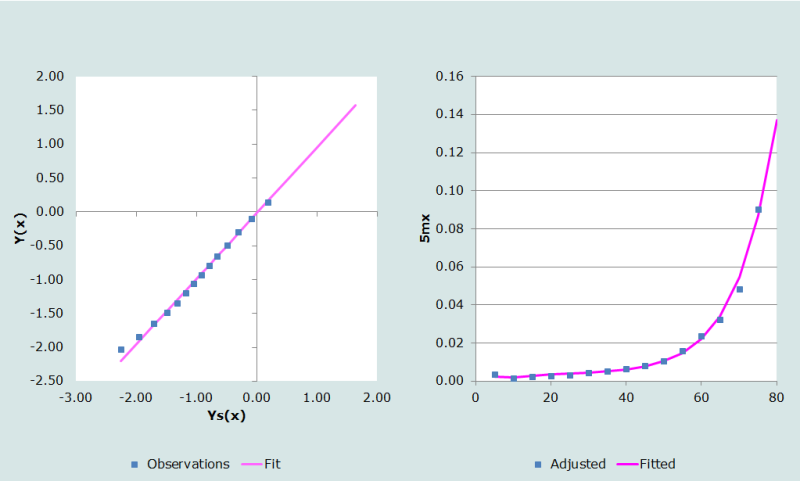
Les coefficients α et β sont respectivement l’ordonnée à l’origine et la pente de la droite de régression liant le logit des probabilités de survie qui apparaissent dans les colonnes 4 et 6 du Tableau 4, pour l’intervalle d’âge choisi par l’utilisateur, comme entre 45 et 75 ans dans cet exemple, soit α = 0,0211 et β = 0,9672.
Ces coefficients sont ensuite appliqués à la transformation logit de la table de mortalité conditionnelle pour fournit les logits lissés qui figurent dans la colonne 7 du Tableau 4. Ainsi, par exemple, le logit lissé à l’âge de 20 ans se calcule comme suit :
Ces valeurs sont ensuite utilisées pour produire la table de mortalité lissée, qui apparaît en colonne 8 du Tableau 4. Par exemple, la valeur à l’âge de 20 ans se calcule comme suit :
Les personnes-années cumulées au-delà de l’âge x dans la table de mortalité conditionnelle, notées Tx, apparaissent en colonne 9 du Tableau 4. Elles sont calculées à partir de la table de mortalité lissée, et ces nombres sont utilisés pour produire les taux de mortalité lissés qui apparaissent en colonne 10 du Tableau 4. Par exemple, pour l’âge de 80 ans :
Diagnostics, analyse et interprétation
Contrôles et validation
L’exemple ci-dessus est tiré du Manuel X des Nations Unies (Division de la Population des Nations Unies 1984), qui donnait une estimation de la complétude de 83% après avoir appliqué cette méthode et celle de Preston et Coale. La différence entre ces estimations antérieures et l’estimation présentée ici (soit 93%) semble due en grande partie à la méthode utilisée pour ajuster la droite et le choix des points retenus pour l’ajustement. La méthode mise en œuvre dans la feuille de calcul (BGB_El Salvador) disponible sur le site web associé à cet ouvrage utilise une régression orthogonale, alors que le Manuel X utilise une procédure plus simple, qui consiste à utiliser des ‘moyennes groupées’ jusqu’à l’âge de 60 ans, et des ‘moyennes tronquées’, ce qui revient en fait à supprimer l’impact du dernier point. Cette différence suggère que l’on pourrait proposer d’ignorer les deux derniers points dans cet exemple puisque la droite de régression est fortement influencée par les points extrêmes sur les axes. Il faut cependant rappeler, comme cela a été noté plus haut, que lorsqu’on utilise une régression orthogonale l’effet d’ignorer ces points reste mineur.
Interprétation
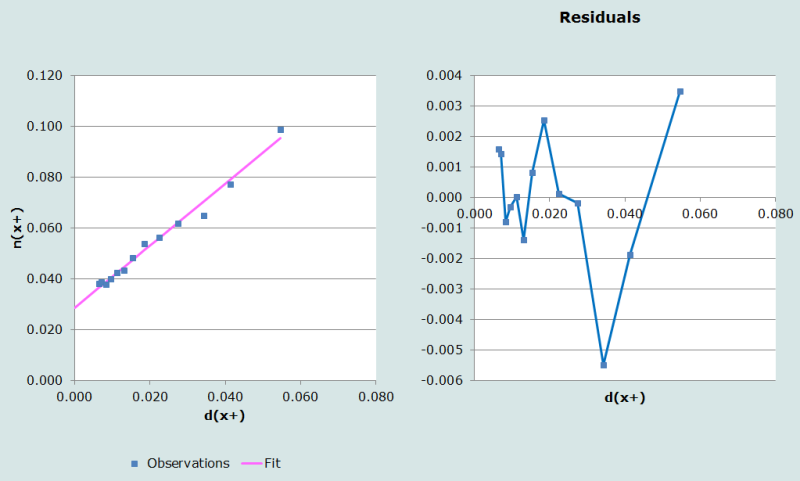
Un problème qui se pose souvent lorsqu’on doit décider quelle limite d’âge supérieure retenir pour ajuster la ligne droite est le fait que la complétude peut varier considérablement du fait de l’exclusion d’un seul point. Par exemple, si on choisit 70 ans et plus comme intervalle ouvert, le graphique permettant de porter un diagnostic ressemblerait à celui qui apparaît dans la Figure 4, et l’estimation de la complétude serait de 82%. En elle-même, ce graphique n’indique pas que l’ajustement est meilleur ou pire que celui obtenu avec le groupe d’âge ouvert de 65 ans et plus. Dans de tels cas, on devrait refaire les calculs pour plusieurs intervalles ouverts, et choisir celui qui est le plus proche de la moyenne ou de la médiane. Dans le cas mentionné ci-dessus, l’estimation de la complétude calculée avec l’intervalle de 60 ans et plus est de 91%, ce qui suggère que l’enregistrement des décès est approximativement complet à 90%. Cependant, comme cela a été mentionné plus haut, on recommande d’une manière générale de ne pas terminer par un groupe d’âge se terminant par zéro dans les populations qui font preuve d’une forte préférence pour les âges se terminant par un chiffre rond.
Problèmes d’interprétation dus à la méthode
Source des données sur les décès déclarés
En général, on doit faire face à deux sortes de problèmes relatifs aux données sur les décès: les cas où le sous-enregistrement (ou le sur-enregistrement) est constant avec l’âge, ce qui est précisément le cas pour lequel la méthode est conçue, et les autres cas, où on observe une complétude variant selon l’âge, qui peut introduire des distorsions dans les estimations. Bien que l’approche générale demeure essentiellement la même quelle que soit la source des données sur les décès, les différentes sources ont chacune leurs propres biais, qui ont un impact sur l’interprétation des résultats. Ces différences sont illustrées ici par des exemples particuliers, mais en règle générale il convient de faire attention aux biais exposés ci-dessous.
1) Données de l’état civil
Lorsque la répartition de la population entre les milieux urbain et rural (ou des catégories semblables) diffère significativement selon l’âge, et que la complétude de la déclaration des décès en milieu urbain est nettement plus forte qu’en milieu rural, alors l’hypothèse que la complétude est indépendante de l’âge est vraisemblablement violée, avec une baisse de la complétude au-delà de 50 ans. Ceci est souvent le cas lorsque une proportion importante de personnes déménagent de l’urbain vers le rural au moment de la retraite. Si on ignore ce fait, on peut obtenir une sous-estimation du niveau moyen de la complétude.
2) Décès déclarés dans les recensements et enquêtes auprès des ménages
Ce type de données est potentiellement sujet à trois problèmes :
- Si une proportion importante de ménages se trouve dissous suite à un décès d’une personne clé (par exemple celui ou celle qui pourvoit aux dépenses), alors les décès de ces personnes seront sous-déclarés, et l’hypothèse de l’indépendance de la complétude avec l’âge ne sera plus vérifiée. Si une proportion importante de décès dans certains groupes d’âge élevés relève de personnes qui ne vivent pas dans des ménages ordinaires, par exemple ceux qui vivent dans des maisons de retraite pour personnes âgées, la violation de l’hypothèse est encore plus forte. Mais ceci n’est pas encore un problème dans la majorité des pays en développement.
- Dans les situations où les jeunes adultes quittent la maison familiale où ils ont grandi pour aller travailler en milieu urbain, il est possible qu’ils soient considérés comme membres de plusieurs ménages (voire d’aucun ménage), et que leur décès soit déclaré plusieurs fois (voire omis), ce qui à nouveau entraine une violation de l’hypothèse de complétude constante par âge. Dans ce cas, on peut en limiter l’effet en ignorant les données en dessous d’un certain âge pour estimer la complétude.
- Il peut souvent y avoir confusion sur la période exacte de référence au cours de laquelle les décès doivent être déclarés, en plus des erreurs sur l’âge au décès. Ce fait peut conduire soit à un sous-enregistrement, soit à un sur-enregistrement des décès. Cependant, lorsque ces biais sont indépendants de l’âge des décédés, cette distorsion sera prise en compte dans l’estimation de la complétude, et ne devrait pas poser de problème pour estimer les taux de mortalité corrigés.
3) Décès enregistrés dans les structures sanitaires
On sait peu de choses sur cette source de données. On peut cependant supposer que la complétude va dépendre de la répartition géographique des structures sanitaires auprès desquelles ces données seront recueillies. Dans de nombreux pays en développement, ces services sont souvent concentrés dans les zones urbaines. Ainsi donc, si la proportion de personnes vivant en milieu urbain plutôt qu’en milieu rural varie selon l’âge, la complétude ne sera de nouveau pas indépendante de l’âge. Il est aussi possible que certaines causes de décès prédominent dans les structures sanitaires, qui, si elles sont importantes quantitativement et sont spécifiques à certains âges, vont probablement violer encore plus l’hypothèse d’indépendance de la complétude constante selon l’âge.
Dans tous ces cas, les points figurant sur le graphique vont se situer de plus en plus au-dessus de la droite de régression aux âges élevés, ce qui risque de conduire à une sous-estimation de la complétude. Mais on pourra améliorer l’estimation en excluant les points qui représentent les âges élevés pour le choix de la droite d’ajustement, quoique l’estimation restera encore biaisée malgré tout.
Description détaillée de la méthode
Exposé mathématique
Quoique la méthode de Brass de la balance de l’accroissement démographique (growth balance method) soit simplement un cas particulier de la méthode généralisée de la balance de l’accroissement démographique (generalized growth balance method), avec un taux de croissance de la population âgée de x années et plus (x+) qui reste constant à tous les âges, il peut être utile de bien décrire ce cas spécifique pour assurer une bonne compréhension.
L’origine de la méthode de Brass de la balance de l’accroissement démographique (Brass 1975) se trouve dans les travaux de Carrier (1958) qui, le premier, proposa une méthode d’estimation de la mortalité en utilisant la distribution par âge des décès. Cette méthode part de la relation que l’on trouve dans l’équation d’équilibre d’une population fermée aux migrations. Dans une telle population, le nombre de personnes dans la population au temps t2 est égal au nombre au temps t1, plus les naissances qui se sont produites entre t1 et t2, et moins les décès qui se sont produits entre t1 et t2, soit : où B sont les naissances et D les décès qui se sont produites entre t1 et t2. Cette équation peut se généraliser à tous les groupes d’âge x+. Ceci suppose que l’on ait une mesure du nombre de personnes qui atteignent l’âge x au cours de l’intervalle de temps situé entre t1 et t2, , ainsi que du nombre de décès d’âge supérieur ou égal à x qui se sont produits entre t1 et t2, noté : La formule devient alors :
(1)
L’équation (1) peut aussi s’écrire :
et en divisant par le nombre de personnes-années vécues au risqué entre t1 et t2, on peut exprimer l’équation de la balance de l’accroissement démographique comme suit :
(2)
où les taux sont calculés comme :
et
On appelle souvent les taux et les ‘taux partiels’ de natalité et de mortalité respectivement, ou parfois les ‘taux segmentiels’ (segmental birth and death rates).
Ces relations ne sont vérifiées que dans le cas où l’enregistrement de la population (c'est-à-dire celle qui atteint son anniversaire) et des décès est complet entre t1 et t2.
Supposons maintenant que toutes les données soient complètes, sauf les décès qui sont enregistrés avec imprécision. Supposons de plus que l’on puisse faire l’hypothèse qu’une proportion constante, notée c, de décès est déclarée, indépendamment de l’âge au décès, pour tous les âges sauf au-delà d’un certain âge et confiné aux personnes adultes. Alors, ou représente le nombre de décès effectivement déclarés d’âge supérieur ou égal à x.
L’équation 2 devient alors:
où
Si l’on suppose en outre que la population est stable, et croissante à un taux annuel constant r, alors l’équation peut être réécrite comme suit : . En conséquence, on doit pouvoir ajuster une ligne droite entre les points de coordonnées: . L’ordonnée à l’origine de la droite donnera la valeur du taux de croissance r, et l’inverse de la pente k donnera la valeur de la complétude de l’enregistrement des décès c.
Les taux de mortalité par groupe d’âge quinquennal, notés, se calculent alors selon la formule :
Mise en œuvre de la méthode
En pratique, on dispose des données suivantes: le nombre de décès déclarés au cours de la période allant de t1 à t2, présentés par groupes d’âge quinquennaux, notés , jusqu’à un dernier intervalle d’âge ouvert au-delà de l’âge A, noté :; et les nombres de personnes dans la population au milieu de la période, présentés selon les mêmes groupes d’âge, notés : jusqu’à . On part de ces données pour effectuer tous les calculs relatifs à la méthode: calcul des effectifs cumulés : et des personnes atteignant leur anniversaire : ou et des personnes-années vécues cumuléesa :
.
Dans le cas où on ne dispose pas de la population en milieu de période, mais seulement à un autre point dans le temps, disons t, on peut tout de même appliquer la méthode avec cette population. La seule différence est que l’estimation de la complétude sera relative à cette population au temps t, comme si elle représentait le milieu de période. En d’autres termes, en supposant la population stable, on a :
et la complétude relative de cette population devient :
.
Les taux de mortalité obtenus en divisant les nombre de décès corrigés pour ce niveau de complétude par fourniront les mêmes taux que les taux que l’on aurait obtenus si on avait utilisé la population par âge au milieu de la période.
Ajustement de la ligne droite
Deux questions se posent pour déterminer la ligne droite qui représente au mieux la relation entre les taux partiels de natalité et de mortalité, à savoir: le choix de la méthode d’ajustement, et le choix des points utilisés pour calculer la pente et l’ordonnée à l’origine.
Ajuster une droite de régression en utilisant la méthode des moindres carrés sans pondération n’est pas recommandé, car la méthode donnerait trop de poids aux valeurs obtenues aux âges élevés qui sont moins fiables. On recommande plutôt d’ajuster une droite en utilisant une méthode plus robuste, comme la droite ‘moyenne’, c'est-à-dire la droite qui joint les points moyens obtenus en répartissant, en fonction de l’âge, les points en deux groupes d’importance égale, et en prenant la moyenne des coordonnées horizontales et verticales de ces deux séries de points. On peut aussi utiliser la méthode de la ‘moyenne tronquée’, c'est-à-dire une méthode analogue à celle de la droite ‘moyenne’, mais où on donne une pondération inférieure aux points qui sont moins fiables, en général les extrémités de l’intervalle. Ces méthodes sont expliquées en détail dans le Manuel X (Division de la Population des Nations Unies 1984). Une autre alternative est décrite en détail dans le Manuel de Nations Unies pour l’estimation de la mortalité adulte (UN Population Division 2002: 105-110). Cette alternative est semblable à celle de la droite ‘moyenne’, mais ici on divise les points en trois groupes de mêmes effectifs, et on détermine la droite qui joint les médianes des points des groupes extrêmes, c'est-à-dire du premier et du dernier tiers.
Mari Bhat signale que chaque méthode a ses points faibles (Bhat 2002). Puisque les taux partiels de natalité et de mortalité sont traités tous deux comme des variables dépendantes, il propose d’utiliser la régression orthogonale comme la meilleure méthode pour tenir compte d’éventuelles erreurs sur les âges. Cette stratégie permet de tenir compte à la fois des distances horizontales et verticales à la ligne de régression, puisqu’elle minimise la somme des carrés des résidus orthogonaux (ORSS), définis comme suit :
.
L’utilisation de cette méthode conduit à calculer la complétude de la déclaration des décès comme le rapport des écarts-types des taux partiels de mortalité et de natalité. La valeur de l’ordonnée à l’origine est la différence entre la moyenne des taux partiels de natalité et la moyenne des taux partiels mortalité divisés par c. C’est cette approche qui est utilisée dans l’application de la méthode de Brass de la balance de l’accroissement démographique présentée dans le classeur Excel disponible sur le site web associé à ce manuel.
Limites de la méthode
Les principales limites de la méthode ont été décrites ci-dessus, et on en tient compte dans la feuille de calcul. Ce sont les conditions suivantes : la population doit être stable et fermée aux migrations. La méthode ne devrait pas être utilisée lorsque ces conditions ne sont pas vraiment remplies. Un bon exemple d’un usage de cette méthode qui serait inapproprié vient des données d’Afrique du Sud, pour les décès déclarés entre le recensement de 2001 et l’enquête dite de communauté de 2007, qui est un recensement sur un large échantillon de population. (Ces données sont présentées dans le classeur Excel : GGB_hommes Sud Africains). Le calcul de la population en milieu de période obtenue en prenant la moyenne des deux recensements donne une estimation de la complétude de 85%. Si on augmente l’âge minimal utilisé pour ajuster la droite à 35 ans, la complétude augmente à 88%, mais reste inférieure à l’estimation obtenue en utilisant la méthode généralisée de la balance de l’accroissement démographique qui donne 91%.
Cette méthode est moins vulnérable aux erreurs sur l’âge que celle proposée par Preston et Coale. En particulier, par exemple, la tendance fréquente à exagérer les âges déclarés au décès (relativement à ceux déclarés au recensement) se manifestera par des points sur le graphique plus à droite (c'est-à-dire situés en-dessous de la ligne) pour tous les âges surestimés. Ces points pourront être éliminés lorsqu’on choisira les points à garder pour ajuster la droite. Par contre, cette méthode est moins vulnérable aux effets de l’écart à la situation stable qui résultent d’une baisse rapide de la mortalité (Martin 1980). Dans ce cas, on tendra à sous-estimer la complétude, car la plus faible mortalité sera interprétée par le modèle comme une augmentation du sous-enregistrement, mesurée par une pente plus forte. Cependant, des simulations ont montré que les biais résultants d’une amélioration lente et régulière de la mortalité, comme certains pays en développement en font l’expérience en l’absence d’épidémie, de famine et de guerre, seront peu importants (Rashad 1978).
En ce qui concerne les changements des taux de fécondité, en supposant que ceux-ci se sont produits au cours des 15 années précédentes, ils auront peu d’impact sur les performances de la méthode car ils ne vont affecter que les groupes d’âges les plus jeunes.
Les migrations vont affecter plutôt la population de jeunes adultes, surtout entre 20 et 35 ans, mais auront moins d’effet sur les décès qui eux se produisent surtout aux âges élevés. Les immigrations dont on ne peut pas tenir compte vont tendre à faire diminuer la pente, et par conséquent à surestimer la complétude de l’enregistrement des décès, et à sous-estimer les taux de mortalité. Par contre, les émigrations dont on ne peut pas tenir compte vont tendre à avoir l’effet inverse. Certains démographes recommandent d’ajuster la ligne droite aussi loin que possible à gauche, jusqu’à l’âge de 5 ans, pour réduire les effets des migrations inconnues. Ceci suppose que les différences de complétude de l’enregistrement des décès entre les enfants et les personnes âgées n’induisent pas de distorsion majeure, car la mortalité est très faible entre 5 et 14 ans. Mais il est peu probable que cette adaptation de la méthode puisse réellement permettre de réduire les biais.
Une stratégie alternative consisterait à limiter les points au-delà de l’âge de 35 ans, de manière à réduire l’essentiel de l’impact potentiel des migrations. Cependant, la qualité des données aux âges élevés est souvent suspecte, ce qui diminue la fiabilité des estimations de la complétude. Il reste possible que ces adaptations produisent de meilleurs estimations que celles obtenues en ignorant les migrations, mais on ne dispose que de peu de recherches sur ce point, et sur la précision des estimations de la complétude obtenues en procédant à de telles adaptations.
D’un point de vue technique, si on dispose de données fiables sur les migrations nettes par âge, on devrait pouvoir adapter la méthode en remplaçant les taux partiels de natalité b(x+) par b(x+) – i(x+), où i(x+) est le taux net de migration dans le groupe d’âge correspondant, pour ajuster une nouvelle ligne droite. Mais en pratique, dans les situations où il faudrait faire cette adaptation, on ne dispose que rarement de données suffisamment fiables de migrations nettes par âge pour justifier cette adaptation.
Les variations de la complétude de l’enregistrement des décès selon l’âge peuvent introduire une courbure dans l’alignement des points du graphique. En conséquence, une des forces de cette méthode est que si les points qui représentent les groupes d’âge successifs sont approximativement situés sur une ligne droite, alors on peut raisonnablement supposer que la complétude est approximativement constante selon l’âge. Mais si certains points sont sur la ligne, et que d’autres en sont éloignés, une méthode pour décider quels points rejeter consiste à calculer le taux partiel de croissance pour chacun des intervalles ouverts successifs, et de garder seulement les points pour lesquels les valeurs de sont assez cohérentes.
Une des principales limites de la méthode est que le graphique liant les taux partiels de natalité et les taux partiels de mortalité, à part les exceptions mentionnées ci-dessus, reste un outil de diagnostic peu performant dans les cas extrêmes. En particulier, la simulation d’une augmentation rapide de la mortalité due au VIH/sida, avec une prévalence de 11% en population générale, à partir d’une population stable, produit des points qui en tous cas sont bien alignés, mais qui conduisent à sous-estimer le niveau de complétude, même si on restreint l’analyse aux âges au-delà de 45 ans. Les leçons à tirer de tout ceci sont que, si les points ne sont pas alignés, on a probablement des données déficientes, mais si les points sont bien alignés on ne peut pas être certain que les estimations de la complétude seront correctes.
Extensions
Lorsqu’on dispose indépendamment de données précises et fiables sur le taux de croissance r, et si la population est stable, alors on peut reformuler l’équation 2 pour estimer c(x+), la complétude de chaque groupe d’âge ouvert, comme suit :
Mais, en pratique il est rare de trouver une population suffisamment stable avec des âges suffisamment précis pour rendre utile cet exercice.
Autres lectures et références
Comme cette méthode est un cas particulier de la méthode généralisée de la balance de l’accroissement démographique, on renvoie le lecteur à la section correspondante pour y trouver des informations complémentaires.
Bhat M. 2002. “General Growth Balance method: A reformulation for populations open to migration”, Population Studies 56(1):23–34. doi: https://dx.doi.org/10.1080/00324720213798
Brass W. 1975. Methods for Estimating Fertility and Mortality from Limited and Defective Data. Chapel Hill NC: Carolina Population Centre.
Carrier NH. 1958. “A note on the estimation of mortality and other population characteristics, given death by age”, Population Studies 12:149–163. doi: https://dx.doi.org/10.2307/2172187
Division de la Population des Nations Unies. 1984. Manuel X. Techniques indirectes d’estimation démographique. New York : Nations Unies, Département des affaires économiques et sociales internationales, ST/ESA/SER.A/81. https://unstats.un.org/unsd/demographic/standmeth/handbooks/Manuel_X-fr.pdf
Martin LG. 1980. “A modification for use in destabilized populations of Brass’s Technique for estimating completeness of death registration”, Population Studies 34:381–395. doi: https://dx.doi.org/10.2307/2175194
Rashad HM. 1978. “The Estimation of Adult Mortality from Defective Registration Data.” Unpublished PhD thesis, London: University of London.
UN Population Division. 2002. Methods for Estimating Adult Mortality. New York: United Nations, Department of Economic and Social Affairs, ESA/P/WP.175. https://www.un.org/esa/population/techcoop/DemEst/methods_adultmort/methods_adultmort.html
- Printer-friendly version
- Log in to post comments
