Estimation indirecte de la mortalité adulte à partir des proportions d’orphelines issues de plusieurs enquêtes ou recensements
Description de la méthode
La méthode de base des proportions d’orphelins permet d’estimer indirectement la mortalité des femmes et des hommes adultes à partir des renseignements donnés par les répondants sur la survie de leurs mères et/ou de leurs pères. Les données nécessaires pour appliquer la méthode proviennent en général des recensements ou des enquêtes. Ces données sont collectées à partir des réponses aux questions simples suivantes : «Votre mère est-elle vivante ?» ou «Votre père est-il vivant ?» En utilisant une estimation de l'âge moyen des mères et des pères à la naissance de leurs enfants dans la population étudiée, il est possible de convertir la proportion des répondants de chaque groupe d’âge dont la mère ou le père est vivant lors de l’enquête en probabilité de survie à l'âge adulte ( pour les femmes et pour les hommes).
Lorsque des données sur les orphelins ont été collectées dans deux enquêtes successives, il est possible de dégager des mesures relatives à la survie des parents entre les deux opérations de collectes, au sein d’une cohorte synthétique, et d’en déduire des paramètres de la table de mortalité pour cette période. En particulier, si les adultes âgés de 15 à 49 ans ont été interrogés sur la survie de leurs parents, on peut estimer les probabilités conditionnelles de survie à partir des données sur les orphelins à l'âge adulte, c'est-à-dire pour les cohortes synthétiques de 20 ans et plus. Les méthodes basées sur des cohortes synthétiques peuvent fournir des estimations de la mortalité adulte pour une période récente et relativement bien définie. Ceci est particulièrement utile dans les pays où l'épidémie du VIH est généralisée et où le niveau de la mortalité des adultes est susceptible d'avoir changé brusquement au cours des deux dernières décennies. L'approche permet potentiellement de réduire également les biais résultant de la sous-déclaration du statut d’orphelin par ceux qui ont perdus leurs parents à un jeune âge.
Si, dans une seule enquête, une question supplémentaire concernant la date de décès des parents a été posée, on peut utiliser cette information pour reconstruire les proportions de répondants dont la mère ou le père était encore en vie quelques années plus tôt et estimer les probabilités de survie des parents dans la période du passé correspondante, de la même manière que pour les données de plusieurs opérations de collecte successives.
Les méthodes basées sur la survie des parents ont un avantage sur les questions directement posées à propos des décès survenus dans les ménages : la mortalité des adultes peut être estimée de cette manière dans les enquêtes de taille modérée. En revanche, seuls les recensements ou les enquêtes à très large échantillons peuvent donner des estimations directes fondées sur les décès au cours des douze mois précédant la collecte qui sont suffisamment précises pour être utiles. En outre, les méthodes basées sur la survie des parents ne reposent pas sur l’hypothèse selon laquelle la population est fermée à la migration. Cependant, les résultats que l’on obtient ne seront pas représentatifs au niveau des petits états ou des régions d’un pays dans lesquelles une proportion importante de la population aura émigré ou sera composée d’immigrés.
Données requises
Pour estimer la mortalité des femmes adultes :
- Les proportions de répondants dont la mère est en vie, classées par groupe quinquennal d'âge du répondant, à deux ou plusieurs dates différentes (ceux qui ne savent pas si leur mère est vivante ou qui n'ont pas répondu à la question devraient être exclus des calculs) ;
- Le nombre de naissances survenues l'année précédant le recensement ou l'enquête classées par groupe quinquennal d'âge de la mère ;
Pour estimer la mortalité des hommes adultes :
- Les proportions de répondants dont le père est en vie, classés par groupe quinquennal d'âge du répondant, à deux ou plusieurs dates différentes (ceux qui ne savent pas si leur père est vivant ou qui n'ont pas répondu à la question devraient être exclus des calculs) ;
- Le nombre de naissances survenues l'année précédant le recensement ou l'enquête classées par groupe quinquennal d'âge de la mère ;
- Une estimation de la différence d’âge entre les hommes et les femmes ayant des enfants, par exemple la différence entre les âges médians des hommes et des femmes actuellement mariés.
Ces tableaux doivent généralement être établis pour les répondants hommes et femmes et les estimations sont faites à partir de deux séries de proportions et pour les deux sexes ensemble.
La méthode des cohortes synthétiques décrite ici produit des estimations de la mortalité adulte à partir des données fournies par les orphelins à l’âge adulte, c'est-à-dire les personnes âgées de 15 ans ou plus. Bien qu'on n’ait pas besoin de données sur les groupes d'âge plus jeunes pour produire les estimations basées sur les cohortes synthétiques, si ces données sont collectées, elles devraient être introduites dans la feuille de calcul en vue de générer les estimations au moyen de la méthode de base des proportions d'orphelins.
Si les poids d’échantillon sont fournis avec les données, il convient de les utiliser de manière appropriée au logiciel statistique utilisé pour produire les tables qui servent d’inputs.
Hypothèses importantes
Une limitation inhérente à la méthode des proportions d’orphelins est que les données relatives à la survie des parents ne peuvent être collectées qu’à partir de leurs enfants survivants au moment de l’enquête. La survie des adultes qui n’ont aucun enfant vivant n’est pas représentée dans les déclarations concernant la survie des parents. En outre, les parents ayant plus d’un enfant survivant sont surreprésentés par rapport à ceux qui ont exactement un enfant survivant, en proportion du nombre de leurs enfants survivants. La méthode produit donc des résultats non biaisés uniquement si la mortalité des parents n’est pas corrélée au nombre de leurs enfants encore en vie au moment de l’enquête. En général, le biais de sélection qui découle des violations de cette hypothèse est faible (Palloni, Massagli et Marcotte 1984). Dans les populations touchées par les épidémies de VIH, ce biais est susceptible d'être plus sévère.
Travaux préparatoires et recherches préliminaires
Avant de commencer l'analyse, il convient de vérifier le nombre de répondants qui ont déclaré qu'ils ne savaient pas si leur mère ou – plus fréquemment - le père était en vie ou qui ont omis de répondre à la question. Le taux de réponse sur ces questions est généralement très élevé et on peut simplement exclure de l'analyse les répondants qui ont répondu «ne sais pas» ou n'ont pas répondu à la question. Ceci revient à supposer que la proportion des parents décédés de ces répondants est la même que pour les parents de ceux qui ont répondu à la question. Cependant, quelques enquêtes ont collecté suffisamment de données incomplètes pour suggérer que le biais de non-réponse pourrait être un problème sérieux. Par exemple, il est possible que la plupart des gens qui omettent de répondre à la question aient des parents décédés. Si tel est le cas, les orphelins non déclarés pourraient représenter une proportion importante de tous les orphelins, en particulier dans les groupes d'âge plus jeunes ; ce qui conduirait à une sous-estimation importante dans les estimations finales de la mortalité adulte.
Un moyen utile de vérifier la qualité des données concernant les orphelins consiste à comparer les réponses de répondants de sexe masculin avec celles des répondantes de sexe féminin de même âge. On ne s’attend pas que la proportion des parents décédés diffère significativement entre les femmes et les hommes de même âge. Si les proportions divergent parmi les répondants plus âgés, cela pourrait refléter les différences entre hommes et femmes dans les erreurs de déclaration des âges ou indiquer que le genre qui déclare moins le décès des parents (généralement les hommes) est plus susceptible de perdre contact avec leurs familles et de supposer à tort que certains parents décédés sont encore en vie.
Lorsque deux ou plusieurs ensembles de données sur la survie des parents sont disponibles, il convient généralement d’estimer indépendamment la mortalité à partir de chaque série de données, à l'aide de la méthode de base des proportions d’orphelins, et de produire également des estimations à partir des données sur les orphelins à l’âge adulte organisées dans des cohortes synthétiques, afin de comparer les trois ensembles de résultats. La feuille de calcul Excel associée à ce chapitre produit les deux types d’estimations, la méthode de base des proportions d’orphelins et la méthode basée sur les cohortes synthétiques.
Précautions et mises en garde
- Les estimations tirées de la méthode des proportions d’orphelins sont des probabilités conditionnelles de survie, c'est-à-dire les probabilités de décéder entre deux âges adultes à condition d'être en vie au début de l'intervalle. Pour obtenir une table de mortalité complète, les estimations de la probabilité de survie de la naissance à l'âge adulte doivent être calculées en utilisant une autre source de données sur la mortalité des enfants.
- Dans diverses applications en Afrique de l'Est et ailleurs, la méthode des proportions d’orphelins a donné des résultats qui indiquent des baisses invraisemblablement rapides de la mortalité et des incohérences flagrantes entre les estimations tirées d’enquêtes successives. Cela semble être dû à «l'effet d'adoption», qui consiste en une sous-déclaration du décès des parents lorsque ce décès est survenu quand ils étaient très jeunes (Blacker 1984; Blacker and Gapere 1988; Hill 1984; Timæus 1986). Dans ces cas, les enfants sont souvent élevés par d'autres parents et sont souvent énumérés comme leurs propres enfants. Cela signifie qu'ils sont énumérés comme ayant un parent en vie ; ce qui peut entraîner des estimations très basses de la mortalité. Au fur et à mesure que les répondants vieillissent, la probabilité s’accroît que, en plus du parent biologique, leur parent d’accueil, le parent adoptif ou beau-parent soit également décédé. Cela implique que le biais est plus prononcé pour les jeunes enfants, dont le parent adoptif est probablement vivant. Les procédures permettant d’estimer la mortalité adulte à partir des données de cohortes synthétiques sur les orphelins à l’âge adulte ont été développées spécifiquement pour résoudre ce problème. Toutefois, ces procédures ne peuvent pas complètement éliminer les biais sur les résultats dans les populations où le nombre d’enfants orphelins est sensiblement sous-déclaré.
- Bien qu’il soit possible de dégage des estimations de mortalité en utilisant des données sur les répondants d’une quarantaine d’années, les parents de plusieurs de ces répondants sont très âgés et ont une mortalité très élevée. Cela signifie que la précision avec laquelle on peut estimer le niveau de mortalité à partir des données sur la survie des parents est par nature beaucoup plus faible qu'elle ne l'est pour les répondants plus jeunes.
- Comme toutes les méthodes qui impliquent l'analyse du changement entre deux enquêtes indépendantes, l’approche basée sur des cohortes synthétiques d’orphelins est vulnérable aux biais résultant de différences dans la qualité des données entre les deux enquêtes. Si les répondants étaient davantage susceptibles de déclarer des parents décédés comme étant vivants dans une des enquêtes, le biais qui résulte de ces erreurs de déclarations sera amplifié dans les estimations obtenues avec la méthode de la cohorte synthétique. La mortalité sera surestimée si trop peu d’orphelins ont été déclarés dans l’enquête réalisée plus tôt et sous-estimée si trop peu d’orphelins ont été déclarés dans l’enquête réalisée plus tard. En outre, les estimations fondées sur la variation de la proportion de parents survivants entre deux enquêtes sont associées à d’erreurs d'échantillonnage plus larges que les deux séries de proportions à partir desquelles elles sont calculées.
Application de la méthode
Étape 1: Calculer l'âge moyen des mères et pères à la naissance de leurs enfants
Pour appliquer la méthode des proportions d’orphelins, on doit disposer d'une estimation de l'âge moyen auquel les parents ont eu leurs enfants afin de contrôler les variations dans l’éventail des âges auxquels ils ont été exposés au risque de décès. L'âge moyen des femmes à la naissance de leurs enfants est généralement calculé à partir des données sur les naissances de l'année précédant l’enquête ou le recensement classifiées par groupe quinquennal d'âge des mères. La mesure est simplement l’âge moyen des femmes ayant eu une naissance, selon la formule suivante, qui ne tient pas compte de la structure par âge de la population :
Dans cette équation, 5Bx représente les naissances des femmes du groupe d’âge entre x et x + 4 ans révolus, et (x + 2) représente le point médian du groupe d'âge des femmes décalé vers le bas d’une demi-année, pour tenir compte du fait que les femmes ayant une naissance au cours de l’année précédant l’interview l’ont eu en moyenne 6 mois plus tôt et qu’elles étaient donc alors 6 mois plus jeunes. Ce calcul peut être fait dans le fichier Excel joint. Si les données utilisées pour calculer sont compilées par âge des femmes à l'accouchement, le point médian de chaque groupe d'âge deviendrait x + 2,5.
Il n'est pas nécessaire d'ajuster les données sur les naissances pour tenir compte des erreurs sur la période de référence, d’autant que les estimations de la mortalité ne sont pas très sensibles à ces erreurs. Cependant, si on a des preuves que la structure par âge de naissances a été sévèrement déformée par une mauvaise déclaration des âges, notamment par les femmes qui ont exagéré leur âge, le nombre de naissances selon l'âge pourrait être recalculé à partir d'une structure par âge de la fécondité ajustée avant le calcul de .
En principe, l'âge moyen à la maternité devrait se référer à la date à laquelle les répondantes sont nées, qui peut correspondre à n'importe quel moment entre 5 et 45 ans avant la collecte des données sur la survie des parents. Une estimation basée sur les données de fécondité collectées dans la première des deux enquêtes qui ont posé des questions sur la survie des parents devrait être adéquate dans des populations qui, en ce moment-là, n’ont pas encore connu une baisse significative de la fécondité. Si l’on pense que le niveau de la fécondité a baissé, et si des données de recensements ou d'enquêtes antérieures existent, des valeurs de pourraient également être calculées à partir de ces données antérieures pour déterminer si cet indicateur a changé. Si c'est le cas, alors, la meilleure façon de déterminer quelles valeurs finales de retenir pour l'estimation de la mortalité adulte dépendra des données disponibles et du type de changement de la fécondité. Une autre option pourrait consister à calculer à partir de données collectées au moment où la fécondité a commencé à baisser et à utiliser cette valeur pour les groupes de répondantes nées à cette période ou plus tôt, puis à utiliser une interpolation linéaire entre cette valeur et celle de l’enquête en cours pour estimer pour les répondantes des plus jeunes groupes d'âge.
L'âge moyen des pères à la naissance de leurs enfants est généralement estimé en ajoutant à l'âge moyen des mères à la naissance de leurs enfants une mesure de la différence d'âge entre les hommes et les femmes ayant des enfants :
Une estimation de cette différence peut être faite à partir des données de recensement, en calculant la différence entre l’âge médian des hommes actuellement mariés et l’âge médian des femmes actuellement mariées. C’est une solution plus appropriée que la différence entre les âges moyens au premier mariage des hommes et des femmes, calculée dans les populations où les dissolutions d’unions et les mariages polygames sont courants. La médiane est utilisée plutôt que la moyenne de sorte que la surestimation différentielle des âges par les répondants âgés, dont la fécondité est vraisemblablement nulle de toute façon, n’affecte pas l’estimation.
Cette méthode d'estimation de l'âge moyen des hommes à la naissance de leurs enfants suppose que les âges des pères d'enfants nés de femmes non mariées sont égaux, en moyenne, aux âges des pères d'enfants nés de mères mariées. Si cette hypothèse n’est pas vérifiée, cette méthode pourrait introduire un biais significatif dans l'estimation de dans les populations où la procréation en dehors du mariage est fréquente. Ce problème est difficile à résoudre mais heureusement, les estimations de la mortalité ne sont pas très sensibles aux erreurs sur l'estimation de .
Étape 2: Calculer les mesures relatives à la survie des parents à l’âge adulte pour les cohortes synthétiques
Le classeur Excel contient des feuilles séparées pour le calcul de ces proportions pour les femmes et les hommes adultes. Les valeurs à introduire dans la feuille Orphelins de mères sont soit le nombre de répondants par groupe quinquennal d’âge dont la mère est en vie et le nombre d’enquêtés ayant répondu à la question, soit directement les proportions des répondants dont la mère est en vie, calculée à partir de ces nombres. De la même façon, les valeurs à introduire dans la feuille Orphelins de pères sont soit le nombre de répondants par groupe quinquennal d’âge dont le père est en vie et le nombre ayant répondu à la question, soit directement les proportions des répondants dont le père est en vie, calculées à partir de ces nombres. Pour la survie des mères comme pour celle des pères, l’ensemble des résultats les plus récents doit être saisi dans le panneau du haut de la feuille de calcul et l’ensemble le plus ancien dans le panneau repris plus bas. Bien que les données puissent concerner les répondantes du sexe féminin, les répondants du sexe masculin ou les répondants des deux sexes, la tabulation doit se faire de la même façon.
Le tableur calcule les paramètres relatifs à la survie des parents dans une cohorte synthétique au moyen de la méthode de « variable r ». Les proportions moyennes des répondants dont les parents sont encore en vie dans la période entre les deux opérations de collecte sont multipliées par l'exponentielle des taux de croissance de ces proportions au cours de la période, qui sont cumulés à partir de l’âge de 20 ans. Ceci «supprime» l'effet de la croissance démographique, produisant ainsi, des proportions qui seraient observées dans une population stationnaire et qui sont relatives à la proportion des répondants avec des parents survivants à partir de l'âge de 20 ans. Ces proportions stationnaires reflètent le taux (ou le rythme) auquel des adultes perdent leurs parents au cours de la période entre les deux opérations de collecte.
La proportion moyenne des répondants d’un groupe d'âge dont la mère (ou le père) est encore en vie au cours de la période entre les deux opérations de collecte est calculée comme ceci :
Où t se rapporte à la première opération de collecte, t + h à la deuxième opération de collecte survenant h années après la première, et une mesure de l’intervalle de temps entre les deux opérations de collecte. Après avoir calculé ces mesures, la proportion moyenne des parents de personnes âgées de 20 ans exacts qui sont vivants au cours de la période peut être estimée comme :
Les taux de croissance, entre la première et la deuxième opération de collecte, des proportions de parents encore en vie par groupe d’âge de répondants, sont calculés comme :
Ensuite, les proportions qui correspondent à une cohorte synthétique d’individus dont les parents vivent toujours, parmi ceux dont les parents étaient vivants quand ces individus avaient 20 ans peuvent être calculées comme :
où τ se réfère à la mesure ajustée (c’est-à-dire, la période) du temps pour la cohorte synthétique.
Étape 3a: Calculer les probabilités de survie conditionnelle de la table de mortalité pour les femmes
La survie des femmes est estimée entre l’âge inférieur de 45 ans et un âge calculé comme 25 + n ans, où n est la limite supérieure de chaque groupe d'âges des répondants. L'équation de régression suivante et les coefficients du tableau 1 sont utilisés:
Par exemple, lorsque n est égal à 30 ans, les probabilités de survie de la table de mortalité sont estimées dans les intervalles de 10 ans à partir de 45 ans jusqu’à l’âge exact de 55 ans, en utilisant les données sur la survie des mères fournies par les répondants du groupe d’âge de 25 à 29 ans.
Tableau 1 Coefficients pour estimer les probabilités de survie des femmes à partir des proportions de répondants dont la mère est encore vivante, parmi ceux dont la mère était toujours vivante quand ils avaient 20 ans
n | a(n) | b(n) | c(n) |
|---|---|---|---|
25 | -0,8623 | 0,00292 | 1,7861 |
30 | -0,3822 | 0,00679 | 1,2062 |
35 | -0,4355 | 0,01197 | 1,1310 |
40 | -0,5995 | 0,01847 | 1,1419 |
45 | -0,7984 | 0,02547 | 1,1866 |
50 | -0,9360 | 0,03039 | 1,2226 |
Source: Timæus (1991) | |||
Étape 3b: Calculer les probabilités conditionnelles de survie de la table de mortalité pour les hommes
Chaque estimation de la survie des hommes est calculée à partir des données relatives à deux groupes d'âge adjacents de cinq ans, et non à partir d’un seul groupe d'âge. La survie des hommes est calculée entre une borne inférieure de 55 ans et une borne supérieure calculée comme 35 + n, où n est le milieu de deux groupes d'âge adjacents. On utilise l'équation de régression suivante et les coefficients indiqués dans le tableau 2 ci-dessous :
Par exemple, lorsque n vaut 40 ans, la probabilité de survie est estimée sur un intervalle de 20 ans, à partir de 55 ans jusqu’à l’âge exact de 75 ans, en utilisant les données sur la survie des pères fournies par les répondants dans les deux groupes d'âge adjacents de 35-39 ans et 40-44 ans.
Tableau 2 Coefficients pour estimer les probabilités de survie des hommes à partir des proportions de répondants dont le père est encore vivant, parmi ceux dont le père était toujours vivant quand ils avaient 20 ans
n | a(n) | b(n) | c(n) | d(n) |
|---|---|---|---|---|
25 | –0,0554 | 0,00757 | 0,0239 | 0,8080 |
30 | –0,7539 | 0,01558 | 0,6452 | 0,6498 |
35 | –1,0809 | 0,02273 | 0,9289 | 0,4807 |
40 | –1,1726 | 0,02647 | 0,9381 | 0,4372 |
Source: Timæus (1991) | ||||
Étape 4: Convertir les probabilités de survie en estimations du niveau général de la mortalité
La série des probabilités de survie conditionnelle, notées npb, et obtenues à partir de différents groupes d'âge de répondants, se réfère à l'intervalle entre les deux enquêtes. Ces probabilités représentent chacune une table de mortalité incomplète avec une base à 45 ans pour les femmes et 55 ans pour les hommes. La série sera dans une certaine mesure erratique à la suite des erreurs de déclarations d'âge, des erreurs d'échantillonnage et d’autres erreurs. Elle peut être lissée en ajustant à partir des probabilités un modèle relationnel logit à 2 paramètres associé à des tables de mortalité. Les logits des probabilités de survie conditionnelle sont calculés de la façon suivante :
Les logits équivalents de la table de mortalité utilisée comme standard sont exprimés comme ceci :
Les paramètres α et β du modèle ajusté correspondent à l’ordonnée à l’origine et à la pente de la droite de régression des valeurs de Yx sur . En principe, les estimations pour les groupes d’âges plus élevés sont moins vulnérables à aux erreurs d'échantillonnage que ceux des groupes d'âges plus jeunes, car elles sont basées sur un nombre plus important de décès de leurs parents. Cependant, ces estimations peuvent indiquer une mortalité plus faible que les estimations faites pour les groupes d'âges plus jeunes ; ceci est probablement dû au fait que les répondantes plus âgées exagèrent souvent leurs âges. Ainsi, on devrait, à chaque extrémité de la série, exclure les estimations qui sont sans commune mesure avec les autres estimations dans les groupes d'âge utilisés pour estimer α et β.
Après avoir calculé α et β, on peut calculer les estimations lissées des probabilités de survie conditionnelle :
Les estimations ajustées des probabilités de survie conditionnelle se réfèrent à une période de temps clairement définie et dépendent peu des hypothèses relatives à la structure par âge de la mortalité sur lesquelles reposent le processus d'estimation. Elles ne seront pas fortement déformées dans les populations avec des structures par âge de la mortalité inhabituelles telles que celles des populations exposées à une épidémie généralisée de VIH. Dès lors, ces probabilités de survie doivent, si possible, être utilisées telles quelles pour les analyses ultérieures. Néanmoins, il est souvent nécessaire de convertir ces estimations relatives aux cohortes synthétiques en un indicateur habituel de mortalité afin de pouvoir mener des comparaisons entre la mortalité des hommes et celle des femmes ou afin de comparer les deux séries d'estimations à d’autres estimations du niveau de la mortalité obtenues à partir de sources alternatives. Cela peut être fait en ajustant une table type de mortalité à 1-paramètre à partir de chaque probabilité de survie conditionnelle pour obtenir l'indicateur désiré à partir du modèle ajusté.
Plusieurs types d'indicateurs du niveau de mortalité ont été utilisés à cette fin, y compris les paramètres de niveau de mortalité de différents systèmes de tables-types de mortalité, des probabilités de survie, des espérances de vie à divers âges entre 5 et 30 ans, et même l'espérance de vie partielle entre 25 et 70 ans, notée 45e25. L’utilisation des paramètres des tables-types a l'avantage de souligner que toute la table de mortalité est estimée par l’ajustement d’un modèle, et non directement mesurée à partir des données observées. Les mesures de l'espérance de vie résument le niveau de mortalité adulte dans son ensemble, alors qu’utiliser les probabilités de survie ou l’espérance de vie entre deux âges adultes permet d’éviter l’extrapolation aux âges élevés des niveaux de mortalité estimés chez les jeunes adultes. De plus en plus, au cours de ces dernières années, les estimations ont été présentées sous forme de probabilités de survie entre les âges exacts 15 et 60 ans, soit par la probabilité 45q15, puisque cette mesure est préférée par plusieurs organismes internationaux comme indicateur de la mortalité des jeunes adultes et des adultes d’âge moyen.
Dans les applications de la méthode des orphelins présentée ici, les probabilités de survie sont converties en paramètre α d'un système relationel logit à un paramètre associé à des tables de mortalité, puis en estimations de la probabilité conditionnelle de décéder dans un éventail plus large d'âges adultes. (Il convient de noter que, même si le même standard est utilisé et si la valeur de β est égale à 1, le paramètre α d'un modèle ajusté à partir de la naissance, ne sera pas le même que la valeur de α qui serait calculée dans les modèles qui auraient été ajustés à des mesures de la probabilité conditionnelle de survie à partir des âges 45 ou 55 ans.)
Le tableur Excel calcule la probabilité conditionnelle de survie entre les âges exacts de 30 et 60 ans (30q30), 15 et 60 ans (45q15), et 50 et 70 ans (20q50). Les deux premiers indicateurs du niveau de mortalité adulte sont utiles pour comparer les estimations faites à partir des cohortes synthétiques avec celles obtenues par la méthode de base des proportions d’orphelins et d'autres mesures de la mortalité des adultes ; le troisième est le plus utile pour comparer les estimations pour les femmes et les hommes, faites à partir des données sur les orphelins à l'âge adulte ou pour évaluer la cohérence interne d'une série de ces estimations sans extrapolation à partir de la survie des âges adultes moyens aux plus jeunes âges adultes. Le paramètre α des modèles à un paramètre sont calculés à partir des estimations de n–20pb selon la formule suivante :
Où les estimations de n–20pb sont obtenus à l'étape 2, avec b = 45 pour les estimations de la survie des femmes et b = 55 pour les estimations de la survie des hommes, et des valeurs de >qui proviennent d'une table-type de mortalité. Ainsi, on obtient une série d'estimations de α correspondant aux mesures de probabilités conditionnelles de survie calculées à partir des différents groupes d'âge. Des valeurs plus élevées de α correspondant à une mortalité plus élevée. Ensuite, pour chaque α, les indicateurs tels que 20q50, 30q30 et 45q15 peuvent être calculés avec l’équation suivante :
Le tableur peut calculer ces indicateurs en utilisant un standard issu soit des tables-types des Nations Unies, soit de l’une des quatre familles de tables-types de Princeton. La standard choisit doit avoir une structure par âge de la mortalité adulte qui ressemble à celle de la population étudiée. Une autre table de mortalité peut être utilisée comme standard si on a des éléments pour affirmer qu'elle ressemble de plus près à la structure de la mortalité des adultes dans la population étudiée. La table de mortalité la plus appropriée peut ne pas être de la famille de modèles qui traduit le mieux la relation entre la mortalité des enfants et la mortalité des adultes. Si on ne sait rien de la structure par âge de la mortalité à l'âge adulte, l'utilisation du modèle général des Nations Unies ou du modèle Ouest des tables de Princeton est recommandée.
Comme les estimations se rapportent tous à la même période, il est logique pour produire une estimation finale de la survie pour la période entre les deux enquêtes en calculant la moyenne d'un ensemble contigu d'estimations qui exclut les valeurs aberrantes obtenues à partir des répondants les plus jeunes et les plus âgés. Ces valeurs aberrantes peuvent être identifiées à l’aide d’une représentation graphique des logits des probabilités de survie conditionnelle présentés en vis-à-vis des logits d’une table standard. Si on observe une tendance à la hausse ou à la baisse des α de tous les groupes d'âge à partir des valeurs ajustées sur un modèle à 1-paramètre, la table standard de mortalité à laquelle les évaluations sont appliquées peut être inappropriée. L'analyste devrait probablement adopter soit une autre table standard de mortalité, soit modifier la vitesse à laquelle la mortalité augmente avec l'âge dans le modèle sélectionné en modifiant le paramètre β.
Étape 5: Calculer la période de référence à laquelle les estimations se rapportent
Chaque probabilité de survie se réfère à la période comprise entre les deux opérations de collecte. On pourrait vouloir leur attribuer une date exacte au sein de cette période, de façon à pouvoir les représenter graphiquement afin de les comparer aux autres estimations de la mortalité adulte. Si l'on suppose un rythme constant d’évolution de la mortalité au cours de la période qui sépare les deux opérations de collecte, on peut considérer que ces probabilités se réfèrent à la moyenne géométrique des dates des deux collectes. La date de chaque opération de collecte peut être calculée comme la moyenne des dates auxquelles les entretiens ont eu lieu ou le point milieu de la période de travail sur le terrain si les dates exactes des entretiens ne sont pas disponibles.
Exemple
Cet exemple, présenté dans la feuille Excel associée à ce chapitre, utilise des données sur la survie des mères et des pères, collectées dans les recensements généraux de la population de 1989 et 1999 au Kenya.
Étape 1: Calculer l'âge moyen des parents à la naissance de leurs enfants
Pour les femmes, l'âge moyen à la naissance des enfants est une moyenne simple de l'âge des femmes ayant donné naissance. Cet âge peut être calculé directement à partir de données individuelles, ou être estimé à partir d'une tabulation de naissances par groupe quinquennal d'âge des mères. Pour cette application, il a été calculé en utilisant les données du recensement général de la population de 1989 (voir tableau 3). Au Kenya, on pourrait aussi utiliser les données des recensements précédents de la population afin de vérifier si l'âge à la naissance des enfants a changé au fil du temps :
Tableau 3 Calcul de l'âge moyen des mères à la naissance de leurs enfants, Kenya, 1989
Groupe d'âge | Naissances de l’année passée B(i) | Milieu du groupe d’âges N | B(i)*N |
|---|---|---|---|
15–19 | 73 600 | 17 | 1 251 200 |
20–24 | 193 400 | 22 | 4 254 800 |
25–29 | 170 220 | 27 | 4 595 940 |
30–34 | 95 180 | 32 | 3 045 760 |
35–39 | 56 340 | 37 | 2 084 580 |
40–44 | 23 240 | 42 | 976 080 |
45–49 | 8 020 | 47 | 376 940 |
Totaux | 620 000 | 16 585 300 |
L'âge moyen des hommes à la naissance de leurs enfants est calculé en ajoutant à l'âge moyen des femmes à la naissance de leurs enfants la différence entre les âges médians des hommes et des femmes actuellement mariées. On peut voir dans le tableau 4, que l'âge médian des hommes actuellement mariés se situe entre le point milieu de la tranche d'âge 30-34 et le point milieu de la tranche d'âge 35-39 ans. Par interpolation linéaire entre ces deux points on a :
Et,
Tableau 4 Âge des femmes et des hommes actuellement mariés, Kenya, 1989
Groupe d’âge | Hommes mariés | Femmes mariées | Proportion cumulée des hommes | Proportion cumulée des femmes |
|---|---|---|---|---|
10-14 | 2 800 | 6 680 | 0,0010 | 0,0019 |
15-19 | 18 040 | 212 060 | 0,0071 | 0,0612 |
20-24 | 173 840 | 623 040 | 0,0664 | 0,2356 |
25-29 | 464 720 | 670 760 | 0,2250 | 0,4234 |
30-34 | 479 460 | 487 180 | 0,3886 | 0,5597 |
35-39 | 406 000 | 387 000 | 0,5272 | 0,6681 |
40-44 | 330 140 | 305 500 | 0,6398 | 0,7536 |
45-49 | 250 540 | 243 120 | 0,7253 | 0,8216 |
50-54 | 212 820 | 189 240 | 0,7979 | 0,8746 |
55-59 | 161 760 | 137 120 | 0,8531 | 0,9130 |
60-64 | 135 060 | 113 860 | 0,8992 | 0,9449 |
65-69 | 101 860 | 75 540 | 0,9340 | 0,9660 |
70-74 | 72 080 | 49 980 | 0,9586 | 0,9800 |
75-79 | 56 240 | 30 100 | 0,9778 | 0,9884 |
80+ | 65 120 | 41 380 | 1,0000 | 1,0000 |
Totaux | 2 930 480 | 3 572 560 |
L'âge moyen des hommes à la naissance de leurs enfants est donc:
Étape 2: Calculer les mesures relatives à la survie des parents à l’âge adulte pour les cohortes synthétiques
Les proportions des Kenyans dont la mère était encore en vie dans l’intervalle intercensitaire des recensements de 1989 et de 1999 sont présentées dans la quatrième colonne du tableau 5. Ces proportions sont les moyennes géométriques des proportions indiquées dans les deux recensements qui sont présentées dans la deuxième et la troisième colonne du tableau 5. Par exemple, dans le groupe d'âge de 25 à 29 ans, on aura :
La proportion des répondants de 20 ans exacts dont la mère est toujours en vie est calculée à partir de ces estimations pour les groupes d'âge de 15-19 ans et 20-24 ans:
Le jour de référence du recensement en 1999 était le 24 août alors que pour le recensement de 1989 il s’agit du 25 octobre. Ainsi, le taux de croissance au cours de la décennie (1989-1999) de la proportion de mères survivantes pour le même groupe d'âge est :
Pour le premier groupe d'âge, le taux de croissance cumulé de 20 ans à 22,5 est égal à :
Pour le deuxième groupe d'âge, le taux de croissance cumulé de 20 à 27,5 ans est égal à :
Tandis que pour le troisième groupe d'âge, il est égal à:
et ainsi de suite.
Les proportions d’individus qui, dans une cohorte synthétique, ont une mère encore en vie parmi ceux qui avaient encore une mère vivante quand ils avaient à 20 ans sont présentées dans la septième colonne du tableau 5. Elles sont calculées à partir des proportions moyennes et des taux de croissance dans les quatrième et cinquième colonnes. Par exemple, pour le groupe d’âge de 25 à 29 ans :
Les calculs effectués dans cette étape pour les données sur les orphelins de père sont identiques et sont présentés dans le tableau 6.
Tableau 5 Estimation de la survie des femmes dans l'intervalle entre les deux recensements et estimations correspondantes de α et de 30q30, à partir des données sur les orphelins de mères à l'âge adulte, Kenya, 1989-1999
Groupe d’âge | Proportion de non-orphelins 1989 5Sn-5(t) | Proportion de non-orphelins 1999 5Sn-5(t+h) | Proportion de non-orphelins 5Sn-5( ) | Taux d’accroi-ssement | Age n | Proportion de non-orphelins 5Sn-5(τ)
| Valeur estimée de l(25+n) l(45) | Valeur ajustée de l(25+n) l(45) | Probabilité de décès (30q30) |
|---|---|---|---|---|---|---|---|---|---|
15-19 | 0,9557 | 0,9336 | 0,9446 |
|
| ||||
20-24 | 0,9233 | 0,9080 | 0,9156 | -0,00170 | 25 | 0,9804 | 0,9669 | 0,9667 | 0,192 |
25-29 | 0,8839 | 0,8771 | 0,8805 | -0,00078 | 30 | 0,9369 | 0,9295 | 0,9291 | 0,172 |
30-34 | 0,8229 | 0,8244 | 0,8236 | 0,00018 | 35 | 0,8751 | 0,8745 | 0,8804 | 0,167 |
35-39 | 0,7553 | 0,7691 | 0,7622 | 0,00184 | 40 | 0,8139 | 0,8240 | 0,8145 | 0,140 |
40-44 | 0,6258 | 0,6685 | 0,6468 | 0,00671 | 45 | 0,7057 | 0,7203 | 0,7244 | 0,140 |
45-49 | 0,5335 | 0,5653 | 0,5492 | 0,00589 | 50 | 0,6184 | 0,6329 | 0,6037 | 0,113 |
Étape 3a: Calculer des probabilités de survie conditionnelle de la table de mortalité pour les femmes
Ces probabilités de survie sont présentées dans la huitième colonne du tableau 5 et sont calculées à partir des proportions reprises dans la septième colonne en utilisant les coefficients de régression présentés dans le tableau 1 et l'estimation de l’âge moyen des mères à la naissance de leurs enfants (26,75 ans) obtenus à l'étape 1. Par exemple, pour les répondantes âgées de 25 à 29 ans, on obtient :
Il est utile de noter que chaque mesure de la table de mortalité est assez proche - en valeur - de la proportion à partir de laquelle elle a été calculée.
Étape 3b: Calculer les probabilités de survie conditionnelle de la table de mortalité pour les hommes
Ces probabilités de survie sont présentées dans la huitième colonne du tableau 6 et sont calculées à partir des proportions reprises dans la septième colonne en utilisant les coefficients de régression présentés dans le tableau 2 et l'estimation de l’âge moyen des pères à la naissance de leurs enfants (32,96 ans) obtenue à l'étape 1. Par exemple, pour l'estimation finale présentés dans le tableau 6, le calcul est le suivant :
Tableau 6 Estimation de la survie des hommes dans l'intervalle entre les deux recensements et estimations correspondantes de α et de 30q30, à partir des données sur les orphelins de père à l'âge adulte, Kenya, 1989-1999
Groupe d’âge | Proportion de non-orphelins 1989 5Sn-5(t) | Proportion de non-orphelins 1999 5Sn-5(t+h) | Proportion de non-orphelins 5Sn-5( ) | Taux d’accroi-ssement | Age n | Proportion de non-orphelins 5Sn-5(τ)
| Valeur estimée de l(35+n) l(55) | Valeur ajustée de l(35+n) l(55) | Probabilité de décès (30q30) |
|---|---|---|---|---|---|---|---|---|---|
15-19 | 0,8670 | 0,8368 | 0,8518 |
|
|
| |||
20-24 | 0,7971 | 0,7730 | 0,7849 | -0,00312 | 25 | 0,9525 | 0,9052 | 0,9045 | 0,259 |
25-29 | 0,7136 | 0,7055 | 0,7096 | -0,00117 | 30 | 0,8519 | 0,7816 | 0,7849 | 0,257 |
30-34 | 0,6071 | 0,6074 | 0,6073 | 0,00004 | 35 | 0,7270 | 0,6395 | 0,6370 | 0,244 |
35-39 | 0,4972 | 0,5198 | 0,5084 | 0,00453 | 40 | 0,6156 | 0,4860 | 0,4678 | 0,225 |
40-44 | 0,3729 | 0,3953 | 0,3839 | 0,00592 |
| 0,4772 |
Étape 4: Convertir les probabilités de survie en estimations du niveau de mortalité
Pour lisser la série d'estimations de probabilités conditionnelles de survie en ajustant un système relationnel logit à 2 paramètres, on calcule d'abord les logits des probabilités. Par exemple, l'estimation de 10p45 pour les femmes obtenue à partir de données sur les répondants âgés de 25-29 est converti de la sorte:
La valeur équivalente pour la table-type de mortalité des Nations Unies (modèle Général) correspondant à une espérance de vie à la naissance de 60 ans est :
En régressant les logit des estimations observées de la survie conditionnelle sur les logits du standards, et en excluant le dernier point (basé sur les répondants âgés de 45-49 ans) qui se situe très bas en dessous de la ligne, on obtient des estimations suivantes : α = -0,3398 et β = 0,8597. Le fait que l'estimation de β est inférieure à 1 indique que la mortalité des femmes au Kenya augmente moins rapidement que ce qui est prévu par le modèle de mortalité standard dans la tranche d'âge de 45 à 75 ans.
Ayant obtenu α et β, la probabilité conditionnelle de survie ajustée pour le second groupe d'âge, par exemple, peut être calculée comme suit :
La série complète des probabilités conditionnelles de survie ajustées est présentée dans la neuvième colonne du tableau 5 pour les femmes et du tableau 6 pour les hommes. En considérant les estimations de 5p45 et 25p45 du tableau 5, la probabilité conditionnelle de décès entre les âges exacts de 50 et 70 ans dans le modèle ajusté à 2 paramètres est égale a : 1 - 0,7244 / 0,9667 = 0,251.
Les estimations de 30q30, la probabilité de décéder entre 30 et 60 ans exacts calculés par l'ajustement des probabilités conditionnelles de survie estimées au modèle à 1-paramètre, sont présentées dans les colonnes les plus à droite du tableau 5 et du tableau 6. Par exemple, la valeur de α calculée à partir de l'estimation de 10p45 pour les femmes donne :
En utilisant cette valeur de α, la mesure correspondante de 30q30 est :
Étape 5: Calculer la période de référence à laquelle les estimations se rapportent
Les estimations de la cohorte synthétique sont des mesures de la mortalité des adultes au cours de la période entre les deux enquêtes. Leur date de référence peut être calculée en faisant la moyenne géométrique des dates de collecte de données sur le terrain des deux enquêtes. Ainsi, en l’appliquant aux recensements de 1989 et de 1999 au Kenya, on obtient :
Diagnostics, analyse et interprétation
Contrôles et validation
Le nombre de répondants qui ont déclaré qu'ils ne savaient pas si leur mère ou leur père était en vie ou qui n'ont pas répondu aux questions doit être vérifié avant d'écarter ces répondants de l'analyse. Si ce nombre est important, les données fournies peuvent ne pas être représentatives de la population dans son ensemble. De plus, un niveau élevé de non-réponse pourrait indiquer que le personnel de terrain ou les enquêtes ont éprouvé des difficultés avec la question sur la survie des parents. Dans ce cas, il est possible que les réponses, même quand elles ont été fournies, ne soient pas fiables. S’il y a un niveau élevé de non-réponse sur une question, il serait utile de déterminer si ces non-réponses sont concentrées sur une minorité d’enquêteurs ou sur certaines catégories de répondants.
Si l’information sur la survie des mères et des pères a été obtenue à la fois de répondants hommes et femmes dans un recensement ou une grande enquête avec des marges d’erreur étroites, il est possible d’établir les proportions de pères et de mères encore en vie séparément pour les répondants de chaque sexe en vue de comparer la cohérence des déclarations. La cohérence des déclarations ne garantit pas leur exactitude, mais des différences statistiquement significatives entre les proportions calculées pour les répondants hommes et femmes impliquent qu’au moins un des deux sexes, et peut-être les deux, donnent des réponses inexactes.
Il est courant de constater que les femmes déclarent des proportions de parents vivants plus basses que les hommes. Certains analystes pensent que c’est parce que les femmes restent en contact plus étroit que les hommes avec leurs parents et que certains hommes disent que leurs parents sont en vie parce qu’ils ne savent pas qu’ils sont en fait décédés. Si cela est vrai, les données obtenues des femmes sont plus exactes que celles obtenues des hommes. Mais il n’y a pas de preuve convaincante qui confirme cette interprétation et d’autres facteurs, en particulier les différences entre hommes et femmes dans les erreurs sur la déclaration de leur âge, peuvent aussi être à l’origine des incohérences dans les proportions déclarées par les hommes et les femmes. De plus, dans les enquêtes ne portant que sur quelques milliers de ménages, les marges d’erreur des estimations pour les premiers groupes d’âge peuvent être larges par rapport aux proportions de mères ou de pères décédés. S’il n’y pas de raison particulière pour privilégier les réponses des femmes, nous conseillons donc d’établir les estimations finales de la mortalité adulte sur les réponses combinées des deux sexes.
Interprétation
Les résultats de l'analyse de données sur les orphelins collectées lors des recensements du Kenya de 1989 et 1999 sont représentés dans la figure 1 ci-dessous. Selon les données du recensement de 1989, la mortalité des adultes au Kenya avait connu un lent déclin dans les années 1970 et au début des années 1980. Les probabilités de décès étaient assez faibles et un écart important existait entre la mortalité des hommes et des femmes. En revanche, les données du recensement de 1999 indiquent que la mortalité a augmenté de façon régulière pour les hommes et les femmes et a atteint un niveau relativement plus élevé entre la fin des années 1980 et le milieu des années 1990.
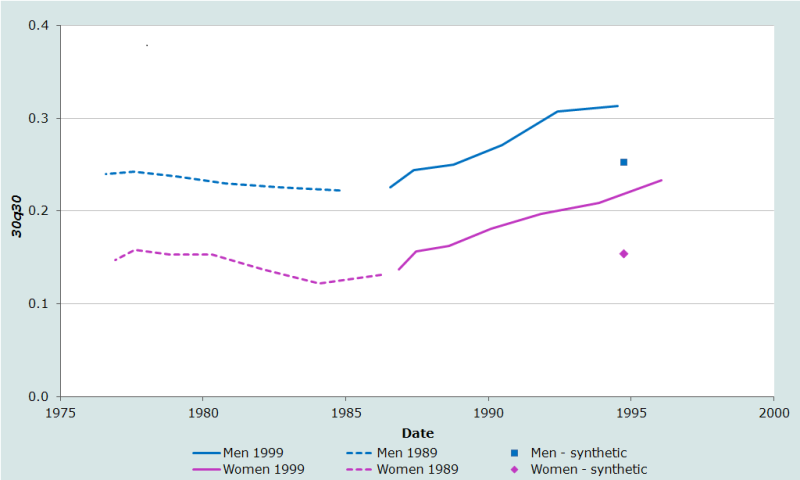
Une caractéristique rassurante de ces résultats est que les estimations de la mortalité pour 1985-1986 obtenues à partir des deux recensements sont cohérentes. Celles du recensement 1989 (les points les plus récents présentés sur les lignes en pointillés) sont basées sur les déclarations relatives à la survie des parents des répondants qui sont encore des enfants. Les estimations obtenues pour une période légèrement plus récente à partir du recensement de 1989 (les premiers points sur les lignes solides) sont estimées à partir des déclarations qui concerne la survie des parents des répondants étaient trentenaires en 1999. Bien que cette cohérence entre les estimations faites à partir des probabilités de survie des parents des répondants de différents âges dans différentes enquêtes ne garantisse pas leur exactitude, les résultats obtenus suggèrent que l’on peut exclure certaines erreurs (mais pas toutes), y compris le biais résultant de l'effet d'adoption. Ce biais est plus sévère pour les estimations effectuées à partir des données sur la survie des parents des jeunes enfants. Plus l’enfant est jeune au moment du décès de ses parents, plus il est probable qu’à la question relative à la survie des parents, il ait été répondu en faisant référence à un parent adoptif ou à un autre parent qui l’a élevé. Quand les répondants avancent en âge, les mauvaises déclarations deviennent proportionnellement moins importantes par rapport à l'augmentation rapide du nombre de décès des parents qui se produisent à la fois à mesure que les répondants et leurs parents vieillissent. Ainsi, si l'effet d'adoption était un problème au Kenya, on s'attendrait à ce que les estimations de la mortalité des adultes relatives au milieu des années 1980 soient plus faibles quand elles sont déduites du recensement de 1989 que lorsqu’elles sont dégagées des données du recensement de 1999.
Si les estimations de la mortalité obtenues auprès des plus jeunes répondants par la méthode basique des orphelins avaient été biaisées à la baisse, on s'attendrait à ce que les estimations tirées des proportions d’orphelins parmi les jeunes adules organisées en cohortes synthétiques soient plus élevées que celles fournies par la méthode basique des orphelins pour les mêmes périodes. Cela n’est toutefois pas le cas au Kenya - elles sont plus faibles.
Ce schéma où les estimations déduites des jeunes adultes et obtenues de cohortes synthétiques sont plus faibles que celles dégagées des déclarations des jeunes enfants de façon classique est inhabituel. Cela reflète probablement l'importance croissante de la mortalité due au sida au Kenya au cours des années 1990. Les estimations des cohortes synthétiques sont principalement basées sur l'expérience des parents âgés de 50 ans et plus, qui n'ont pas été touchés fortement par l'épidémie du sida. Ainsi, en utilisant des tables-types de mortalité classiques pour déterminer 30q30 à partir des différentes probabilités, on sous-estime la mortalité adulte, car, la mortalité dans les groupes d’âge de 30 à 50 ans est plus faible dans ces tables qu’au Kenya.
En revanche, les parents des jeunes répondants, dont on déduit les estimations les plus récentes par la méthode de base des proportions d’orphelins, ont pour la plupart entre 30 à 40 ans, ce qui correspond au groupe d’âge où la mortalité par sida connaît son niveau le plus élevé. Ainsi, utiliser des tables-types de mortalité classiques pour déterminer 30q30 à partir de ces données produit une surestimation, car la mortalité des 50 à 60 ans supposée dans ces tables est plus élevée qu’au Kenya.
Les estimations des cohortes synthétiques appuient cette interprétation : dans cette application, la probabilité conditionnelle de décès baisse entre 30 et 60 ans quand l’âge des enquêtes augmente aussi bien pour les femmes que pour les hommes (voir le tableau 5 et le tableau 6). Ceci suggère que la mortalité est relativement élevée chez les plus jeunes dans la tranche d'âge de 45 à 75 ans et relativement faible aux vieux âges au Kenya par rapport au modèle général des tables-types des Nations Unies. Ceci pourrait aussi indiquer une mortalité élevée liée au sida chez les plus jeunes adultes. La valeur réelle de la probabilité 30q30 vers le milieu des années 1990 se situe probablement quelque part entre les estimations produites par les deux variantes de la méthode des orphelins. En utilisant un modèle standard de mortalité par âge qui augmente plus lentement avec l'âge, en fixant le paramètre β de la table type de mortalité à 0,7 et en recalculant α, on produit un ensemble d’indicateurs de mortalité adulte pour les deux sexes ayant une meilleure cohérence interne. Il permet également de réduire les incohérences entre les estimations de cohortes synthétiques et la plupart des estimations les plus récentes obtenues à partir des données du recensement de 1999 en utilisant la méthode de base des proportions d’orphelins. Ainsi, la probabilité de décéder entre 30 et 60 ans au Kenya dans les années 1990, toujours conditionnée au fait d’avoir survécu jusqu’à 30 ans, était probablement d'environ 20 pour cent pour les femmes et 30 pour cent pour les hommes.
La figure 2 présente une seconde application de l’approche reposant sur des cohortes synthétiques pour analyser deux ensembles de données sur les orphelins recueillies dans deux opérations de collecte successives. Il s’agit des données des recensements des Îles Salomon de 1986 et de 1999. Dans cette application, l’indice de mortalité présenté sur le graphique est la probabilité de décéder entre 15 et 60 ans, conditionné au fait d’avoir survécu jusqu’à 15 ans (45q15). Un contraste évident apparaît immédiatement entre ces séries d'estimations et celles du Kenya ou celles des pays arabes dont les résultats sont présentés dans la discussion sur la méthode de base des proportions d’orphelins. En effet, on remarque que les inégalités par sexe de mortalité adulte sont faibles aux Îles Salomon.
L’application de la méthode fournit une preuve évidente de problèmes de la qualité des données recueillies dans le recensement de 1986. Premièrement, les estimations suggèrent que la mortalité a connu une baisse très rapide, mais les estimations les plus récentes de la série la plus ancienne, déduites des données qui concernent les enfants, indiquent une mortalité sensiblement plus faible que les estimations faites pour quelques années plus tard à partir des données recueillies auprès des enquêtés plus âgés dans le recensement de 1989. Les incohérences de ce genre indiquent généralement que les estimations sur les données du premier recensement (1986) sont trop basses parce que l’effectif des enfants orphelins est sous-estimé en raison de l'effet d'adoption. Dans la mesure où la tendance à sous-déclarer les enfants orphelins peut être une caractéristique persistante de la culture d'une population, ces incohérences jettent ainsi un doute sur les estimations les plus récentes faites à partir des données collectées au recensement suivant. Le deuxième problème avec les estimations du recensement de 1986 aux Îles Salomon est qu’elles suggèrent que les femmes ont une mortalité adulte plus élevée que les hommes. C’est une situation très atypique.
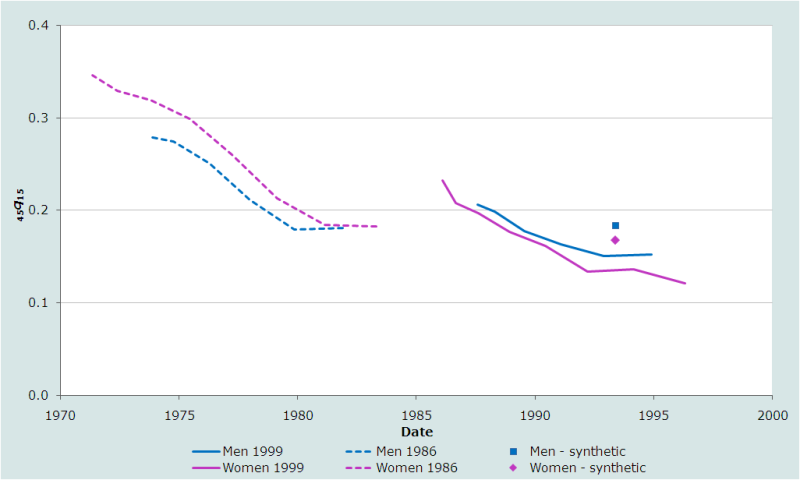
Les estimations faites pour le début des années 1990 à partir des proportions d’orphelins parmi les jeunes adultes organisées dans des cohortes synthétiques appuient l'idée selon laquelle les estimations calculées à partir des données recueillies sur les enfants en 1999 sont également trop faibles. Les estimations obtenues à l’aide des cohortes synthétiques sont probablement les plus fiables puisqu’elles sont basées exclusivement sur les données des orphelins adultes. Ainsi, on peut provisoirement conclure que la probabilité de décéder entre 15 et 60 ans aux Îles Salomon est passée de 30 pourcents environ au début des années 1970 à 17,5 pourcents sur l’espace de deux décennies.
Description détaillée de la méthode
Introduction
Des méthodes simples et robustes pour estimer la mortalité à partir des données relatives à des cohortes d’orphelins et recueillies dans une seule opération de collecte ont d'abord été publiées par Brass and Hill (1973). Zlotnik and Hill (1981) ont été les premiers à souligner qu’à partir du moment où les questions «Votre mère est en vie? » ou «Votre père est vivant? » ont été posées au sein d’une même population dans deux enquêtes successives, il devient possible de calculer des mesures relatives à la survie des parents au sein de cohortes synthétiques et obtenir ainsi des indices qui reflètent la mortalité des adultes dans la période entre les deux enquêtes. Puisque ces estimations sont faites à partir des changements survenus au niveau de la survie des parents entre les deux enquêtes, les indicateurs de mortalité adultes qui en découlent sont vulnérables aux différences entre enquêtes en matière d’erreurs de déclaration et d’erreurs d'échantillonnage. Toutefois, la période de référence des mesures est généralement plus récente que celle des deux autres séries d’estimations simplement basées sur les proportions d’orphelins observées dans les cohortes prises individuellement.
Les données des cohortes synthétiques ont un autre avantage : si les décès survenus au cours de la période entre les deux enquêtes sont tous complètement déclarés, les omissions de décès plus éloignés dans le passé n'auront pas d'impact sur les résultats. Ainsi, les données des cohortes synthétiques sur la survie des parents sont potentiellement moins vulnérables à «l’effet d'adoption» que les données des cohortes simples prises individuellement, à cause de la sous-déclaration des très jeunes enfants orphelins par les enquêtés. Ceci est important, car, l'effet d'adoption est le biais majeur affectant la méthode des proportions d’orphelins; ce biais explique les résultats invraisemblables et les incohérences entre enquêtes successives observées dans un certain nombre d'applications de cette méthode. La façon la plus simple de corriger ces biais est d'analyser uniquement les données sur les orphelins adultes en les organisant dans des cohortes synthétiques (Timæus 1991). On peut le faire en construisant une cohorte synthétique qui débute à 20 ans exacts et combine les données sur la survie des parents collectées au cours de deux opérations successives. Cette cohorte indique la proportion de la population adulte dont les mères ou les pères resteraient en vie s’ils étaient exposés à la mortalité du moment, parmi ceux qui, à 20 ans exacts, avaient une mère ou un père encore vivant. Une telle cohorte synthétique peut être construite uniquement à partir des données relativement fiables fournies par les jeunes adultes.
Timæus (1991) propose d’utiliser 20 ans comme base de la cohorte pour deux raisons. Tout d'abord, ce choix minimise la possibilité de sous-estimer les proportions d’orphelins à cet âge de base et par conséquent, il permet d’éviter une surestimation des proportions d’orphelins et de la mortalité des adultes aux âges suivants. Deuxièmement, parce que l'information sur deux groupes d'âge est nécessaire pour estimer la survie des parents à l'âge exact séparant les groupes, cette approche permet d'appliquer la méthode aux données recueillies dans les enquêtes dans lesquelles seules les femmes âgées de 15 à 49 ans sont interrogées sur la survie de leurs parents.
La généralisation à toutes les populations des relations établies par la théorie des populations stables (Preston et Coale 1982) entre les structures par âge de la population, l’accroissement démographique et la mortalité offre un moyen pratique pour construire de telles cohortes synthétiques. Les mesures sur la survie des parents organisées dans des cohortes synthétiques et correspondantes à une population stationnaire peuvent être obtenues en ajustant les proportions observées des parents survivants en utilisant les taux de croissance des proportions par âge, pour éliminer l'impact des tendances passées de la mortalité. Lorsque les données proviennent de deux enquêtes, l'ajustement en utilisant les taux d’accroissement de la survie des parents par âge a un avantage par rapport aux méthodes qui combinent les changements survenues au niveau des cohortes ; elles sont faciles à appliquer lorsque l’intervalle entre les enquêtes ou recensements ne sont pas de cinq ou dix ans.
Exposé mathématique
Preston et Coale (1982) montrent que dans une population fermée répartie par âge, on peut établir l’équivalence suivante:
(1)
où N(a, t) est le nombre d'individus d’âge a à l'instant t, et μ(z, t) et r(z, t) représentent respectivement l’intensité de mortalité et le taux de croissance à l'âge z et au temps t. L’attrition qui caractérise la population d’individus dont la mère ou le père est vivant, notée NO, peut être décomposée en deux composantes : la mortalité des parents et la mortalité de la population elle-même (Preston and Chen 1984; Timæus 1986):
où π(z, t) représente le taux instantané de perte des parents, et rNO(z, t) le taux de croissance de la population dont les parents survivent toujours, à l'âge z et au temps t. En supposant que les orphelins et le reste de la population soient exposés aux mêmes risques de mortalité et en utilisant le fait que N(0,t)≡NO(0,t), le rapport de l’expression pour les non-orphelins sur celle pour la population totale donne :
(2)
Dans cette équation, le terme de gauche représente la probabilité stationnaire qu'une personne d’âge a ait une mère ou un père vivant, noté S(a,τ), tandis que NO(a,t)/N(a,t) est égale à la proportion non corrigée équivalente, S(a,t). Avec des données d'enquêtes, il est plus commode de travailler avec le taux de croissance de la proportion de la population dont les parents sont vivants, rs(z,t), qu’avec son équivalent, rNO(z,t) - r(z,t), qui est la différence entre les taux d'accroissement pour les non-orphelins et ceux de la population totale.
Au-dessus de n’importe quel âge, la population peut être considérée comme étant autonome (self-contained) et la relation entre la structure par âge, le taux de croissance, et l’intensité de la mortalité indiquée dans l'équation (1) sera toujours valable pour ces populations définies par un âge de départ. Ainsi, en utilisant les notations déjà établies, on a :
pour a> 20. Lorsque les deux côtés sont divisés par S(20,t), cela donne :
Sous sa forme discrète, pour les groupes d'âge x à x + 5, on a :
Mise en œuvre de la méthode
Afin de simplifier l'estimation des mesures de la table de mortalité à partir de ces proportions (Timæus 1991) a développé des modèles de régression pour la mortalité des hommes et des femmes, en estimant les coefficients à partir des données sur la survie des parents dans le même ensemble de populations simulées que celles utilisées dans la méthode de base des proportions d’orphelins (Timæus 1992).
La proportion de personnes âgées d’âge a qui ont une mère survivante, notée S(a), peut être calculée comme la moyenne des probabilités de survie chez les mères qui ont donné naissance à chaque âge y, pondéré par la proportion de naissances qui se produisent à l’âge y (Brass and Hill 1973) :
où l’intégrale couvre toute la population en âge de procréer de s à ω ans. La division de S(a) par S(20) pour a > 20, annule le dénominateur. Ainsi, la proportion d’individus d’un groupe d’âge quinquennal dont les mères sont encore vivantes, parmi ceux qui avaient une mère survivante quand ils avaient 20 ans exactement s’exprime comme :
(3)
pour x ≥ 20. La proportion équivalente d’individus dans chaque groupe d'âge dont les pères survivent est :
(4)
où f(y) représente le calendrier de la fécondité par âge et l(a) correspond aux survivants de la table de mortalité des hommes plutôt que celle des femmes, les âges de procréation s et ω étant aussi ceux des hommes.
Les équations 3 et 4 peuvent être évaluées numériquement en utilisant des tables-types de mortalité et des schémas de fécondité par âge. On peut ensuite ajuster un modèle de régression qui prédit des probabilités de survie à partir des données simulées sur la survie des parents. L'équation d'estimation utilisée pour les orphelins de mère après 20 ans est analogue à celle proposée pour les orphelins depuis la naissance (Timæus 1991, 1992). Cette équation est basée sur l'observation selon laquelle, la proportion de répondants dont les mères sont vivantes, équivaut à une probabilité de survie , où N est l'âge des répondants et B est proche de l'âge moyen à la naissance des enfants, mais dépend aussi de N (Brass and Hill 1973). Pour les applications pratiques cependant, il est plus commode d’ajuster légèrement les proportions sur base de l'âge moyen à la naissance des enfants et d’estimer les probabilités de survie à partir d’un âge de base arrondi, b, situé près de B, et pour une durée d'exposition n, qui est un multiple de cinq ans. En outre, pour les orphelins après l'âge de 20 ans, l'exposition commence 20 ans après l’âge B. Ainsi, la probabilité de survie est estimée à partir d'un âge de référence de 45 ans et l'équation utilisée pour faire les estimations prend la forme suivante :
L'équation équivalente donne parfois des résultats médiocres pour les hommes. Des estimations plus précises peuvent être obtenues si l'information sur la survie des pères dans deux groupes d’âge adjacents est utilisée pour estimer la mortalité. Si les schémas par âge de la mortalité et de la fécondité diffèrent des schémas généraux reflétés dans les coefficients de régression, les proportions de répondants dont le père est vivant dans le groupe d’âge supérieur et celles du groupe d’âge inférieur sont altérées dans des directions qui se compensent en comparaison à la proportion de pères survivant pour l’âge qui sépare les deux groupes d’âge (Timaeus 1992). Si l'on estime les mesures de la table de mortalité à partir des données sur deux groupes d'âge, pour une durée d'exposition égale à l’âge qui les sépare, on réduit la sensibilité des résultats aux variations de la pente de la relation entre la survie des parents et les survivants de la table de mortalité. L'âge moyen à la naissance des enfants des hommes dans les pays en développement est légèrement inférieur à 35 ans en moyenne. Ainsi, les probabilités de survie peuvent être estimées à partir des orphelins après 20 ans en utilisant 55 ans comme âge de référence et un modèle de la forme:
Les coefficients pour les différents groupes d'âge définis par n sont présentés dans le tableau 1 et le tableau 2.
Extensions de la méthode
Masquelier and Timæus (2024) ont développé une méthode alternative à celle décrite en détail ici, spécifiquement conçue pour les populations faisant face à une épidémie généralisée de VIH. Cette méthode repose sur les proportions d'orphelins observées dans des cohortes synthétiques. Le modèle de régression a été étendu pour inclure des coefficients prenant en compte la prévalence et les tendances de l'infection au VIH dans la population, ainsi que, le cas échéant, la couverture des traitements par la thérapie antirétrovirale au moment de la collecte des données.
En plus de l'analyse des données sur les orphelins issues de deux opérations de collecte en utilisant les cohortes synthétiques, Chackiel et Orellana (1985) soulignent que l’on peut recueillir des données dans une seule enquête pour produire des estimations récentes de la même manière. En plus des données habituelles sur la survie des parents, il est pour cela nécessaire de disposer d’informations sur les dates de décès des parents. Par exemple, l'enquête pourrait poser des questions sur l'année et le mois où le parent est décédé, ou sur le nombre d’années écoulées depuis son décès. Si les dates de décès des parents sont rapportées avec une précision raisonnable, cette information peut être utilisée pour reconstruire la proportion des enquêtés qui avaient des parents vivants cinq et dix ans plus tôt. À partir de ces données transversales successives, on peut construire des indices relatifs à la survie des parents organisés dans des cohortes synthétiques formellement identiques à celles générées à partir des données recueillies dans une série d'opérations de collecte distinctes. Ces indices peuvent ainsi être analysés en utilisant la procédure d'estimation de la mortalité à partir des données de plusieurs enquêtes sur les orphelins à l’âge adulte décrite ici.
Assez peu d'enquêtes ou de recensements ont tenté de recueillir des informations sur la date de décès des parents. La qualité des réponses a été très faible pour certaines d'entre elles, mais dans d'autres enquêtes, les dates de décès pour la décennie précédent l’enquête est du plus grand intérêt analytique, car elles semblent avoir été très bien déclarées. Une approche alternative pour distinguer les parents décédés récemment et qui pourrait générer de meilleurs résultats consiste à demander si les parents sont décédés avant ou après un autre événement du cycle de vie, tel que le mariage ou la naissance du premier enfant du répondant.
Les méthodes pour produire des estimations de mortalité à partir de données de ce type sont décrites avec d'autres méthodes d'analyse de données sur les orphelins obtenues d'une seule enquête ou recensement.
Autres lectures et références
La méthode de base des proportions d’orphelins est présentées dans tous les manuels classiques d’estimation indirecte (Sloggett, Brass, Eldridge et al. 1994; Division de la Population des NU. 1984. ) mais, à l’exception de celui des Nations unies sur l’estimation de la mortalité adulte (UN Population Division 2002), ces manuels s’attachent à l’ancienne variante de la méthode, qui recourt à des facteurs de pondération pour obtenir des indices de tables de mortalité, plutôt qu’à la méthode fondée sur la régression, couramment utilisée aujourd’hui. Les méthodes fondées sur la régression ont été proposées précédemment pour les femmes (Hill and Trussell 1977; Palloni and Heligman 1985), mais elles ont été développées pour les hommes plus récemment par Timæus (1992). Ce dernier article passe aussi en revue des contributions plus anciennes sur le sujet et présente les bases théoriques de la méthode.
Les méthodes permettant d’organiser les données sur la survie des parents dans des cohortes synthétiques et d’estimer la mortalité adulte sur cette base ont été proposées dans les années 1980 (Chackiel et Orellana 1985; Timæus 1986; Division de la Population des NU 1984; Zlotnik et Hill 1981). La version de cette approche qui met l'accent sur les orphelins après 20 ans et qui est décrite ici a été proposée par Timæus (1991). Masquelier and Timæus (2024) ont développé une méthode alternative spécifiquement conçue pour les populations faisant face à une épidémie généralisée de VIH.
Blacker JGC. 1984. "Experiences in the use of special mortality questions in multi-purpose surveys: the single-round approach," in Data Bases for Mortality Measurement. New York: United Nations, pp. 79-89. https://www.un.org/development/desa/pd/sites/www.un.org.development.desa.pd/files/publications/mortality/mortality_1984_databasesformortalitymeasurements.pdf
Blacker JGC and JM Gapere. 1988. “The indirect measurement of adult mortality in Africa: results and prospects,” in African Population Conference, Dakar, 1988. Liège: International Union for the Scientific Study of Population, Vol. 2:3.2.23–38.
Brass W and K Hill. 1973. “Estimating adult mortality from orphanhood,” in International Population Conference, Liège, 1973. Liège: International Union for the Scientific Study of Population, Vol. 3:111–123.
Chackiel J and H Orellana. 1985. “Adult female mortality trends from retrospective questions about maternal orphanhood included in censuses and surveys,” in International Population Conference, Florence, 1985. Liège: International Union for the Scientific Study of Population, Vol. 4:39–51.
Division de la Population des NU. 1984. Manuel X. Techniques indirectes d’estimation démographique. New York : Nations Unies, Département des affaires économiques et sociales internationales, ST/ESA/SER.A/81. https://unstats.un.org/unsd/demographic/standmeth/handbooks/Manuel_X-fr.pdf
Hill K. 1984. "An evaluation of indirect methods for estimating mortality," in Vallin, J, Pollard John H and L Heligman (eds). Methodologies for the Collection and Analysis of Mortality Data. Liège: Ordina, pp. 145-176.
Hill K and TJ Trussell. 1977. "Further developments in indirect mortality estimation", Population Studies 31(2):313-334. doi: https://dx.doi.org/10.1080/00324728.1977.10410432
Masquelier, B and IM Timæus. 2024. "Estimating adult mortality based on maternal orphanhood in populations with HIV/AIDS". Population Studies: 1-21. doi: https://doi.org/10.1080/00324728.2024.2416185
Palloni A and L Heligman. 1985. "Re-estimation of structural parameters to obtain estimates of mortality in developing countries", Population Bulletin of The United Nations 18:10-33. https://www.un.org/development/desa/pd/sites/www.un.org.development.desa.pd/files/files/documents/2020/Jan/un_1986_population_bulletin_18.pdf
Palloni A, M Massagli and J Marcotte. 1984. "Estimating adult mortality with maternal orphanhood data: analysis of sensitivity of the techniques", Population Studies 38(2):255-279. doi: https://dx.doi.org/10.1080/00324728.1984.10410289
Preston SH and N Chen. 1984. Two Census Orphanhood Methods for Estimating Adult Mortality, with Applications to Latin America.
Preston SH and AJ Coale. 1982. "Age structure, growth, attrition and accession: A new synthesis", Population Index 48(2):217-259.
Sloggett A, W Brass, SM Eldridge, IM Timæus, P Ward and B Zaba. 1994. Estimation of Demographic Parameters from Census Data. Tokyo, Japan: United Nations Statistical Institute for Asia and the Pacific.
Timæus I. 1986. "An assessment of methods for estimating adult mortality from two sets of data on maternal orphanhood", Demography 23(3):435-450. doi: https://dx.doi.org/10.2307/2061440
Timæus IM. 1991. "Estimation of mortality from orphanhood in adulthood", Demography 28(2):213-227. doi: https://dx.doi.org/10.2307/2061276
Timæus IM. 1992. "Estimation of adult mortality from paternal orphanhood: a reassessment and a new approach", Population Bulletin of The United Nations 33:47-63. https://www.un.org/development/desa/pd/sites/www.un.org.development.desa.pd/files/files/documents/2020/Jan/un_1992_population_bulletin_33.pdf
UN Population Division. 2002. Methods for Estimating Adult Mortality. New York: United Nations, Department of Economic and Social Affairs, ESA/P/WP.175. https://www.un.org/development/desa/pd/sites/www.un.org.development.desa.pd/files/files/documents/2020/Jan/un_2002_methodsestimatingadultmort.pdf
Zlotnik H and KH Hill. 1981. "The use of hypothetical cohorts in estimating demographic parameters under conditions of changing fertility and mortality", Demography 18(1):103-122. doi: https://dx.doi.org/10.2307/2061052
- Printer-friendly version
- Log in to post comments
