Estimation de la fécondité à partir des accroissements de parité des cohortes

Description de la méthode

Les tableaux sur le nombre d’enfants déjà nés par groupe quinquennal d’âge classique des femmes pour un seul recensement ou une seule enquête donnent une information abondante sur la fécondité passée des femmes. Malheureusement, si la fécondité a évolué, les parités moyennes des femmes des différents groupes d’âge ne permettent pas d’estimer le profil par âge de la fécondité, ni par cohorte, ni par période.

Si l’information sur le nombre d’enfants déjà nés existe dans deux recensements ou enquêtes à cinq ou dix ans d’écart environ, la variation du nombre moyen d’enfants déjà nés dans une cohorte de femmes reflète leur fécondité au cours de la période intercensitaire. Il devient alors possible d’estimer la distribution de la fécondité par âge pour cette période. Arretx (1973) a développé une méthode pour utiliser une telle information quand les deux sources sont séparées de 10 ans. Le Manuel X (Division de la Population des NU 1984) présente une variante d’une démarche proposée par Coale et Trussell recourant au quotient P/F. Nous proposons une amélioration par rapport à la présentation du Manuel X, en nous appuyant sur le modèle relationnel de Gompertz.

La méthode consiste à estimer les taux moyens de fécondité par âge de la période intercensitaire, en construisant les parités moyennes d’une cohorte fictive intercensitaire. Une distribution de fécondité cumulée est alors calculée par interpolation à partir de ces parités, et les taux de fécondité par âge sont obtenus à partir de la fécondité cumulée grâce à une suite de soustractions.

La méthode est conçue pour des situations où on peut calculer des parités moyennes par groupe d’âge des femmes en deux points du temps à peu près séparés de dix ans. Si l’intervalle entre les deux recensements est de cinq ans, les femmes d’un groupe quinquennal d’âge à la seconde date sont les survivantes des femmes dans le groupe quinquennal cinq ans plus jeune à la première date. L’accroissement de parité moyenne de la cohorte entre le premier et le second recensement reflète sa fécondité entre les deux recensements, si on peut supposer que la descendance des femmes qui sont décédées ou qui ont migré entre temps n’était pas, en moyenne, systématiquement différente de celle des femmes qui sont restées. En cumulant les accroissements de parité, on peut estimer les parités moyennes d’une cohorte fictive qui aurait, au long de sa vie féconde supposée, les taux de fécondité par âge de la période intercensitaire. Si cette période est de 10 ans, un groupe quinquennal à la seconde date est composé des survivantes des femmes du groupe quinquennal dix ans plus jeunes à la première date. Dans ce cas, il est encore possible de calculer l’accroissement de parité de chaque cohorte pour construire les parités moyennes d’une cohorte fictive. La méthode s’applique aux données provenant entièrement ou partiellement d’enquêtes nationales sur des échantillons représentatifs aussi bien qu’à des données de recensement, car bien que les individus enquêtés d’une cohorte donnée ne soient pas les mêmes aux deux dates, leurs parités moyennes sont représentatives des parités de la population féminine échantillonnée.

Il n’est pas nécessaire que les deux séries de données se réfèrent à deux points séparés par cinq ou dix ans exactement. A moins que la fécondité soit en train d’évoluer très rapidement, des intervalles de quatre ou onze ans fourniront par exemple des estimations raisonnables. Dans ces cas, on ne suit plus une cohorte d’une enquête à l’autre, mais cela n’est pas très important puisque la parité moyenne d’un groupe d’âge ne change pas rapidement d’une année à l’autre.

Bien que la force de la méthode réside dans sa robustesse en cas de modifications de la fécondité, la technique que nous présentons ici peut aussi permettre d’estimer les taux de fécondité par âge lorsqu’on utilise les données d’un seul recensement ou d’une seule enquête, à condition que la fécondité n’ait pas changé au cours de la vie reproductive des femmes concernées.

Hypothèses

La plupart des hypothèses sont celles associées au modèle relationnel de Gompertz, à savoir

• Le standard de fécondité choisi pour la procédure d’ajustement reflète bien la forme de la distribution de la fécondité dans la population.
• Les variations de la fécondité ont été progressives et régulière et elles ont affecté tous les groupes d’âge à peu près de la même manière.
• Les jeunes femmes entre 20 et 30 ans ont déclaré correctement leurs parités.

On suppose en outre que la mortalité et la migration n’ont eu aucun effet sur les distributions effectives par parité ; c’est-à-dire qu’on suppose que la parité moyenne des femmes qui sont décédées ou ont migré entre les deux enquêtes ne diffère pas significativement de la parité moyenne aux mêmes âges des femmes survivantes et présentes en fin de période.

Travail préparatoire et recherches préliminaires

Avant d’entreprendre l’analyse des niveaux de la fécondité par cette méthode, les chercheurs doivent s’interroger sur la qualité des données au moins dans les domaines suivants :

• la structure par âge et sexe de la population; et
• les parités moyennes, après application de la correction d’el Badry si nécessaire.

Précautions et mises en garde

On gardera présentes à l’esprit les mises en garde concernant l’utilisation des informations sur les enfants déjà nés dans les estimations de fécondité. Même dans les pays où les données sont par ailleurs bonnes, les femmes âgées ont tendance à omettre de déclarer certains de leurs enfants, sans doute ceux qui sont décédés ou ceux qui ont quitté le foyer parental. En conséquence, il arrive fréquemment que les parités moyennes ne s’accroissent pas à un rythme vraisemblable ou même qu’elles décroissent au-delà de 35 ou 40 ans. Les taux de fécondité calculés à partir de parités affectées par de telles omissions tendent à sous-estimer la fécondité aux âges élevés. Les effets peuvent ne pas être très visibles si l’erreur est relativement mineure. Les estimations de fécondité fondées sur les parités moyennes des femmes âgées doivent donc être interprétées avec prudence, en particulier si elles font apparaître une fécondité relativement faible par rapport à celle estimée à partir des déclarations des jeunes femmes. Les parités moyennes d’une cohorte fictive sont, en outre, très sensibles aux variations dans la déclaration des parités d’un recensement à l’autre, et leur calcul constitue en conséquence un intéressant test de cohérence des données initiales.

Quand il existe des données supplémentaires sur la fécondité récente, on doit préférer à la méthode décrite ici la procédure qui compare les taux de fécondité intercensitaires cumulés aux parités moyennes d’une cohorte fictive en utilisant un modèle relationnel de Gompertz synthétique; cette seconde méthode est en effet moins sensible à l’omission d’enfants déjà nés dans les déclarations des femmes âgées.

Application de la méthode

Les deux premières étapes sont les mêmes que celles de la méthode relationnelle synthétique de Gompertz.

Etape 1: Calcul des parités moyennes déclarées à partir de chaque recensement

Calculer les parités moyennes ${}_5{P}_x(t_1)$ et ${}_5{P}_x(t_2)$ des femmes de chaque groupe d’âge [x, x + 5) aux deux recensements (t₁ et t₂), pour x =15, 20 … 45 si cela n’a pas déjà été fait lors des recherches préliminaires ou à l’occasion de l’application de la correction d’el Badry. Pour faciliter l’exposé, nous désignons par [[wysiwyg_mathjax:1208:] la parité moyenne dans le groupe d’âge i au temps t où i= (x/5 – 2). Les parités moyennes tirées du premier recensement (ou enquête) sont notées P(i,1) et celles tirées du second P(i,2).

Etape 2: Calcul des parités moyennes pour une cohorte fictive

Le mode de calcul des parités dépend de la longueur de l’intervalle entre les deux recensements.

a) Intervalle de cinq ans

Si l’intervalle entre les deux séries de données est de cinq ans, les survivantes du groupe d’âge i au premier recensement appartiennent au groupe d’âge i+1 au deuxième, et l’accroissement de parité entre les deux recensements est égal à P(i+1,2) - P(i,1). Ces accroissements peuvent être calculés pour chaque groupe d’âge, et les parités de la cohorte fictive sont alors obtenues par cumul des accroissements successifs. Ainsi, si on désigne par$$\Delta P(i+1)$$ l’accroissement de parité pour la cohorte du groupe d’âge i aux premier recensement, et par P(i,s) la parité du groupe d’âge i dans la cohorte fictive (où  renvoie à ‘synthétique’), on a

$$\Delta P(i+1)=P(i+1,2)-P(i,1)$$

pour i=1,…, 6, et donc

$$P(i,s)={\displaystyle \sum _{j=1}^i\Delta P(j)}$$.

On considère que l’accroissement de parité $$\Delta P(i+1)$$ pour le groupe d’âge le plus jeune (i = 0) est égal à P(1,2), en supposant que P(0,1), parité moyenne des femmes de 10-14 ans au premier recensement, est nulle. Si la fécondité évolue rapidement, cette valeur de $$\Delta P(1)$$ reflète donc des taux du moment plus proches de l’enquête que du milieu de l’intervalle, donnant un poids une peu exagéré à l’évolution de la fécondité.

b) Intervalle de dix ans

Si la période entre les recensements ou les enquêtes est de 10 ans, les survivantes de la cohorte appartenant au groupe d’âge i lors de la première enquête seront dans le groupe d’âge (i+2) lors de la seconde. Les parités de la cohorte fictive sont alors obtenues en cumulant deux séries parallèles d’accroissements de parité. Une fois encore, pour les groupes d’âge les plus jeunes, on considère que $$\Delta P(1)$$ est égal à P(1,2) et que $$\Delta P(2)$$est égal à P(2,2). Les autres accroissements de parité sont égaux à $$\Delta P(i+2)=P(i+2,2)-P(i,1)$$ pour i=1,…, 5. 

Les parités de la cohorte fictive pour les groupes d’âge ayant un numéro pair sont obtenues en cumulant les accroissements de parité pour les groupes d’âge ayant un numéro pair, alors que ceux pour les groupes d’âge ayant un numéro impair sont obtenus en cumulant les accroissements de parité pour les groupes d’âge ayant un numéro impair. Donc

$$\begin{array}{l}P(1,s)=\Delta P(1)=P(1,2)\\ P(2,s)=\Delta P(2)=P(2,2)\\ P(3,s)=\Delta P(1)+\Delta P(3)\\ P(4,s)=\Delta P(2)+\Delta P(4)\\ P(5,s)=\Delta P(1)+\Delta P(3)+\Delta P(5)\\ P(6,s)=\Delta P(2)+\Delta P(4)+\Delta P(6)\\ P(7,s)=\Delta P(1)+\Delta P(3)+\Delta P(5)+\Delta P(7)\end{array}$$

Les étapes suivantes reprennent celles déjà décrites lors du recours au modèle relationnel de Gompertz, mais en ajustant une droite sur les données de parité seulement.

Etape 3: Ajustement d’un modèle relationnel de Gompertz

En cas de cohérence interne des données de parité, les points représentant z(i) - e(i) en fonction de g(i) sont alignés sur une droite. On doit exclure du modèle les P-points dont la position s’écarte de la droite. Une régression linéaire ordinaire (par les moindres carrés) permet d’ajuster des droites sur les P-points et d’identifier, les uns après les autres, ceux qui ne s’ajustent pas nettement sur une droite. L’objectif est de rechercher la combinaison du plus grand nombre de P-points qui s’alignent (à peu près) sur la même droite, et de les utiliser pour ajuster le modèle.

Les points sont retenus dans l’ajustement selon les règles suivantes :

• Une série de points contigus doit être incluse dans le modèle. Seuls des points extrêmes peuvent être exclus. (La raison est que chaque point sur le graphique est le résultat d’un calcul de ratio entre les valeurs de données adjacentes. Si l’analyse conduit à considérer une donnée comme non fiable en tant que dénominateur, il n’est pas logique de l’accepter comme numérateur du ratio suivant.)
• Il vaut mieux éliminer les P-points aux âges avancés plutôt qu’aux jeunes âges car les données y sont généralement moins fiables et présentent moins de cohérence entre descendance et fécondité récente.
• Un ajustement réalisé sur un nombre élevée de points est préférable à celui réalisé sur un plus faible nombre moins de points, même s’il est légèrement moins bon.

Etape 4: Evaluer la qualité des paramètres estimés

Les valeurs de α et β, qui représentent la droite de meilleur ajustement joignant les P-points et les F-points restants, nécessitent un contrôle pour vérifier qu’elles ne s’éloignent pas de leurs valeurs centrales de telle manière que le choix du standard serait mis en cause. Un bon ajustement est obtenu si -0,3 < α < 0,3, et si 0,8 < β < 1,25.

Si les paramètres se situent en dehors de ces intervalles, une au moins des séries de données sous-jacentes pose problème ou le standard est inadéquat. Il convient alors d’essayer un autre standard ou de modifier la sélection des points avant de procéder plus avant. Si les paramètres restent en dehors aux intervalles ci-dessus, il faut considérer que la méthode est inappropriée.

Etape 5: Taux de fécondité par âge et indice synthétique de fécondité ajustés

Une fois estimés les deux paramètres du modèle, ceux-ci peuvent être appliqués au standard des parités pour fournir des valeurs ajustées $$Y(i)=\alpha +\beta .Y^s(i)$$ .

. Celles-ci sont ensuite ramenées à des mesures de la proportion cumulée de fécondité réalisée par groupe d’âge i, grâce à la transformation anti-gompit. Les anti-gompits fondés sur les distributions de parité indiquent la proportion de fécondité réalisée dans le groupe d’âge. En divisant la parité observée dans chaque groupe d’âge par ces proportions, on obtient une série d’estimations de l’indice synthétique de fécondité. La moyenne de ces valeurs calculée sur le sous-ensemble des groupes d’âge qui ont été utilisés pour estimer α et β donne l’estimation ajustée de l’indice synthétique de fécondité, $\widehat{T}$ .

En appliquant les mêmes α et β aux gompits standards pour les âges qui bornent les groupes d’âge conventionnels (c’est-à-dire 20, 25 …50 ans), en appliquant la transformation anti-gompit, et en multipliant par $\widehat{T}$, on obtient une distribution de la fécondité cumulée aux divers âges. En faisant la différence entre les estimations successives de la fécondité cumulée et en la divisant par cinq, on obtient une distribution de fécondité ajustée pour les groupes d’âge conventionnels (15-19, 20-24 etc.).

On considère que ces taux de fécondité par âge s’appliquent au point médian de la période entre les deux enquêtes.

Exemple

Nous utilisons les données sur les parités moyennes tirées des recensements du Kenya en 1989 et 1999, comme dans l’exemple sur le modèle relationnel synthétique de Gompertz. Mais dans cette application on suppose qu’on ne dispose d’informations que sur les parités moyennes, pas sur la fécondité récente. Le processus d’ajustement du modèle relationnel de Gompertz aux données de parité est, pour l’essentiel, le même que pour le modèle relationnel de Gompertz de base. L’exposé insiste donc sur les différences entre les deux procédures. La méthode est mise en œuvre dans un dossier Excel.

Etape 1: Calcul des parités moyennes déclarées à partir de chaque recensement

Une correction d’el Badry a été appliquée aux données du recensement de 1989. De toute évidence, les résultats du recensement de 1999 ont été corrigés : il n’y a pas de données manquantes sur la parité. Les parités moyennes tirées des deux recensements figurent aux deux premières colonnes du tableau 1. Les descendances des femmes âgées ont reculé d’environ 0,6 enfant au cours de la décennie. Mais l’accroissement de la descendance des adolescentes est un peu surprenant.

Etape 2: Calcul des parités moyennes pour une cohorte fictive

La période intercensitaire est de 10 ans (entre 1989 et 1999). Nous suivons donc la procédure décrite à l’étape 2(b) pour calculer les parités moyennes des cohortes, qui figurent dans la dernière colonne du tableau 1.

Tableau 1 Parités moyennes par groupe d’âge, Kenya, recensements de 1989 et 1999

Comme indiqué à l’étape 2(b), $$\Delta P(1)=P(1,2)=0,2848$$ et $$\Delta P(2)=P(2,2)=1,3640$$

, alors que

$$P(5,s)=\Delta P(1)+\Delta P(3)+\Delta P(5)=0,2848+(2,6073-0,2416)+(5,3867-3,2138)=4,8234.$$

On voit aisément que d’importantes omissions ont dû affecter les parités aux âges élevés, puisque la parité dans la cohorte fictive à l’âge le plus élevé est inférieure à la parité des femmes dans la cohorte fictive intercensitaire âgée de 40-44 ans.

La définition de l’âge de la mère n’a aucune incidence sur la méthode. Les parités moyennes sont – par définition – celles qui prévalent à la date de l’enquête ou du recensement.

Etape 3: Ajustement d’un modèle relationnel de Gompertz

On utilise les données de la cohorte fictive à la dernière colonne du tableau 1 pour estimer la fécondité au moyen du modèle relationnel de Gompertz. Les points de données (P-points) fondés sur les parités moyennes sont éliminés l’un après l’autre jusqu’à ce que les points restants soient alignés avec les parités (transformées) du schéma de fécondité standard. Les points ajustés sont représentés sur la figure 1.

Image

Figure 1 Fitted P- points, hypothetical cohorts, 1989 and 1999 Kenyan census data

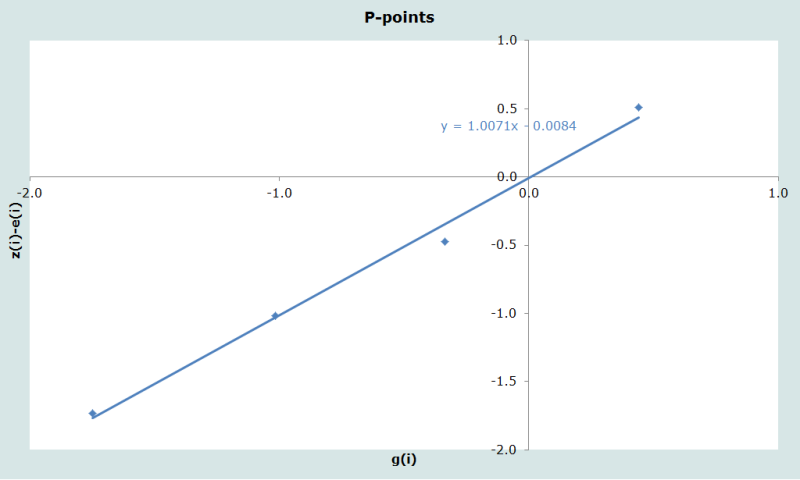
Seuls cinq points de parité peuvent être représentés puisque la parité supposée pour le groupe 45-49 ans est moindre que pour le groupe 40-44 ans (5,4987 contre 5,6041), ce qui signifie que le gompit du rapport entre ces deux points n’est pas défini. L’examen de ces points fait apparaître une sous-déclaration de la fécondité aux âges qui servent à déterminer le dernier point représenté. L’élimination de ce point entraine une nette réduction de l’écart quadratique moyen ; le modèle est donc ajusté sur les quatre points restants.

Etape 4: Evaluer la qualité des paramètres estimés

Il en résulte des valeurs de α et β égales respectivement à -0,0084 and 1,0071. Le schéma de fécondité est donc proche de celui qui sous-tend le standard modifié par Zaba.

Etape 5: Taux de fécondité par âge et indice synthétique de fécondité ajustés

On applique ces paramètres aux gompits des parités du standard, en utilisant le modèle relationnel linéaire $Y(i)=\alpha +\beta Y^s(i)$. En prenant les anti-gompits (colonne 4 du tableau 2) et en divisant par ceux-ci les parités observées aux âges choisis pour l’ajustement du modèle, on obtient une série de cinq estimations de l’indice synthétique de fécondité (comprises entre 5,4 et 5,7 enfants par femme). Leur moyenne ($\widehat{T}$) est de 5,54 enfants par femme.

Tableau 2 Calcul de l’indice synthétique de fécondité estimé (T-chapeau), Kenya, recensements de 1989 et 1999

On applique les estimations ajustées de α et β aux gompits du standard, Y^s(x), dans chaque groupe d’âge pour obtenir les gompits ajustés. On en déduit les anti-gompits qui, multipliés par $\widehat{T}$<, donnent la distribution cumulée de fécondité modifiée, FM(x). La différence entre deux cumuls consécutifs, divisée par cinq donne la série finale des taux de fécondité par âge à la dernière colonne du tableau 3.

Tableau 3 Calcul de la distribution finale de fécondité ajustée, Kenya, recensements de 1989 et 1999

L’indice synthétique de fécondité estimé est de 5,53 enfants par femme ; il s’applique à mi-chemin entre les deux recensements. Dans cet exemple, les taux de fécondité par âge tirés des parités de la cohorte fictive peuvent être comparés à ceux obtenus par l’application du modèle relationnel synthétique de Gompertz (indice synthétique = 5,56 enfants par femme). La proximité des deux séries de résultats est rassurante.

Il faut toutefois se souvenir que les résultats peuvent être sérieusement biaisés si les mères omettent de déclarer des enfants déjà nés, et en particulier si l’ampleur de ces omissions varie d’une enquête à l’autre.

Description détaillée de la méthode

La méthode décrite ici est une variante du modèle relationnel de Gompertz, mais, au lieu d’utiliser des données de parité et de fécondité recueillies en un point du temps, elle élabore un schéma de fécondité ‘moyen’ fondé sur les descendances déclarées en deux points du temps et utilise celles-ci – seules – pour déterminer une distribution de fécondité. L’exposé mathématique complet du modèle relationnel a déjà été présenté.

Variantes de la méthode

Une option de la feuille de calcul permet de choisir une période intercensitaire égale à zéro. Ceci permet de calculer un indice synthétique de fécondité à partir d’une seule série de données de parité. Pour que les estimations produites soient plausibles, il ne suffit pas que les parités moyennes aient été déclarées correctement, il faut aussi que la fécondité se soit maintenue constante sur une longue période avant le recensement ou l’enquête.

Autres lectures et références

L’essentiel de l’exposé de la méthode est donné par Arretx (1973) et mis à jour dans le Manuel X (Division de la Population des NU 1984). La version donnée dans le Manuel X s’appuie sur la méthode du quotient P/F pour convertir les accroissements de parité en taux de fécondité ; la méthode présentée ici recourt à la méthode relationnelle de Gompertz, qui est plus souple.

Arretx C. 1973. "Fertility estimates derived from information on children ever born using data from censuses," in International Population Conference, Liège 1973. Vol. 2. Liège: International Union for the Scientific Study of Population, pp. 247-261.

Division de la Population des NU. 1984. Manuel X. Techniques indirectes d’estimation démographique. New York : Nations Unies, Département des affaires économiques et sociales internationales, ST/ESA/SER.A/81. https://unstats.un.org/unsd/demographic/standmeth/handbooks/Manuel_X-fr.pdf