Le modèle multi-exponentiel de migration

 Description de la méthode

Ce chapitre explique comment ajuster un modèle multi-exponentiel de migration à des données observées sur les migrations.

Depuis une trentaine d’années, ce modèle, conçu par Rogers et Castro (1981), s’est révélé remarquablement efficace pour la représentation des structures par âge typiques des migrations. En général, on observe les mêmes structures par âge, qu’il s’agisse des migrations internationales et interrégionales dans leur ensemble ou des migrations relatives à une région particulière. La fonction multi-exponentielle a été élaborée pour exprimer la relation entre la migration et l’âge, et elle le fait au travers d’une série additive de composantes exponentielles à 7, 9, 11 ou 13 paramètres, selon le degré de complexité du schéma de migration et de l’aptitude des données à supporter une paramétrisation croissante.

Appliqué à une série de taux de migration par année d’âge, le modèle de Rogers-Castro fournit une expression optimale et nuancée de la structure par âge de la migration, qui peut servir à lisser une série de taux de migration observés et que l’on peut utiliser directement pour améliorer la compréhension de la dynamique des migrations. Ce résultat peut trouver de nombreuses autres applications, par exemple dans la mise au point de schémas de migration utilisables dans des projections de population multirégionales. Dans l’idéal, on disposera d’indices de migration par année de calendrier et année d’âge, auxquels on ajustera le modèle de Rogers-Castro. Mais, si – comme c’est souvent le cas dans les pays en développement, où la piètre qualité des données de base peut faire obstacle au développement de calculs aussi minutieux – les données ne sont disponibles que par groupes quinquennaux d’âge, on doit estimer par interpolation des taux par année d’âge au moyen de l’une des méthodes décrites ci-après, avant de tenter l’ajustement par un modèle de Rogers-Castro.

Données requises et hypothèses

Tabulations nécessaires

• Probabilités ou taux de migration par année d’âge (ou, si ce n’est pas possible, par groupes quinquennaux d’âge) de 0 à un âge supérieur à 65 ans.

Idéalement, les données devraient se présenter sous forme de taux par année d’âge. Quand elles sont réparties en groupes quinquennaux d’âge, il faut estimer leurs valeurs par année d’âge au moyen d’une interpolation, avant de tenter l’ajustement par une fonction multi-exponentielle. Le choix de l’âge maximum est quelque peu arbitraire, mais la borne supérieure des données utilisées pour l’ajustement d’un modèle devrait, au moins, être supérieure à l’âge modal de la retraite.

Hypothèses importantes

Le recensement national le plus récent dénombre avec exactitude la population par région de résidence et par lieu de naissance, et identifie les personnes qui ont migré d’une région à l’autre depuis une certaine date antérieure (par exemple le recensement précédent).

Travaux préparatoires et recherches préliminaires

Avant de mettre en œuvre cette méthode, il faut examiner la qualité des données sur au moins deux aspects :

• la structure par âge de la population (éventuellement par région) ; et
• le degré de couverture des recensements (éventuellement par région).

Mise en garde

La méthode ne doit être appliquée aux données de migration nette qu’avec précaution, car la distribution multi-exponentielle des taux par âge modélise les flux migratoires bruts (c’est-à-dire les entrées ou les sorties), mais pas automatiquement les migrations nettes, à moins que l’un des deux flux ne soit nettement plus important que l’autre à tous les âges.

Présentation générale du modèle multi-exponentiel de migration

La fonction multi-exponentielle a été élaborée par Rogers et Castro (1981) pour exprimer le lien entre la migration et l’âge. La migration est généralement forte au cours de la première année de vie ; elle chute jusqu’à un minimum au début de l’adolescence, pour augmenter rapidement jusqu’à son maximum au début de l’âge adulte, après quoi elle diminue, sauf un éventuel sursaut autour de l’âge de la retraite, suivi d’une reprise de la baisse. Dans certains cas, on peut observer une dernière remontée aux âges les plus avancés (Rogers et Castro 1981 ; Rogers et Watkins 1987).

Depuis une trentaine d’années, le système de modélisation de la migration de Rogers-Castro s’est révélé remarquablement efficace pour la représentation des structures par âge des migrations (Little et Rogers 2007 ; Raymer et Rogers 2008 ; Rogers et Castro 1981 ; Rogers et Castro 1986 ; Rogers et Little 1994 ; Rogers, Little et Raymer 2010 ; Rogers et Raymer 1999 ; Rogers et Watkins 1987). Les mêmes structures par âge des migrations ont été observées pour des régions de taille différente et pour des sous-populations distinguées selon le sexe et le groupe ethnique (Rogers et Castro 1981). On les a observées tant dans le cas des migrations interrégionales dans leur ensemble que pour les migrations relatives à une région particulière. Un flux migratoire unidirectionnel (de la région i vers la région j) présente également la même structure. Par exemple, le modèle de Rogers-Castro a été appliqué avec succès aux flux migratoires intercommunaux (entre local authorities) en Angleterre (Bates et Bracken 1982 ; 1987), entre zones métropolitaines et non-métropolitaines au Canada (Liaw et Nagnur 1985), entre régions au Japon, en Corée et en Thaïlande (Kawabe 1990), et au niveau national en Afrique du Sud et en Pologne (Hofmeyr 1988 ; Potrykowska 1988).

Appliqué à une série de taux de migration par année d’âge, le modèle de Rogers-Castro fournit une expression optimale et nuancée de la structure par âge de la migration, qui peut être caractérisée par 7, 9, 11 ou 13 paramètres, selon le degré de complexité de cette structure et la robustesse des données. De plus, les fluctuations aléatoires, souvent associées à l’imprécision des taux par âge observés, sont aplanies.

Des modèles de Rogers-Castro ont été utilisés pour réaliser des projections de population au Canada (George 1994), et appliqués à des périodes, des régions ou des sous-populations dont les données migratoires étaient insuffisantes ou inexistantes (Rogers, Little et Raymer 2010).

Dans sa forme la plus complète et la plus complexe, le modèle multi-exponentiel compte 13 paramètres. Si on appelle M(x) le taux de migration à l’âge x, le modèle complet est défini par :

$$\begin{array}{c}M\left(x\right)=a_1\exp \left(-{\alpha }_{1}x\right)\\ +a_2\exp \left\{-{\alpha }_2\left(x-{\mu }_2\right)-\exp \left[-{\lambda }_2\left(x-{\mu }_2\right)\right]\right\}\\ +a_3\exp \left\{-{\alpha }_3\left(x-{\mu }_3\right)-\exp \left[-{\lambda }_3\left(x-{\mu }_3\right)\right]\right\}\\ +a_4\exp \left({\lambda }_{4}x\right)\\ +c.\end{array}$$

Il comporte cinq composantes additives. La première, $$a_1\exp \left(-{\alpha }_{1}x\right)$$, est une fonction exponentielle négative représentant le schéma de migration aux âges qui précèdent l’entrée sur le marché du travail. La deuxième, $$a_2\exp \left\{-{\alpha }_2\left(x-{\mu }_2\right)-\exp \left[-{\lambda }_2\left(x-{\mu }_2\right)\right]\right\}$$, est une fonction unimodale asymétrique à gauche qui décrit le schéma de migration par âge des personnes d’âge actif. La troisième, $$a_3\exp \left\{-{\alpha }_3\left(x-{\mu }_3\right)-\exp \left[-{\lambda }_3\left(x-{\mu }_3\right)\right]\right\}$$, est presque une courbe en cloche représentant la fonction de migration par âge après la retraite, quand les migrations augmentent brusquement au moment de la retraite avant de décliner à nouveau. Associée à celle-ci, la quatrième composante, $$a_4\exp \left({\lambda }_{4}x\right)$$, est une fonction exponentielle positive qui concerne la migration par âge après la retraite dans les quelques cas où l’on constate une hausse générale de la migration à cette époque de la vie. On peut observer ce phénomène, par exemple, aux États-Unis, avec les personnes âgées du Nord-Est qui migrent vers les États de la sunbelt du Sud-Est et du Sud-Ouest. La dernière composante est un terme constant, c, qui représente les migrations « résiduelles ».

Les recherches effectuées jusqu’à présent ont identifié quatre familles de modèles multi-exponentiels (Rogers, Little et Raymer 2010) ; une seule d’entre elles, qui présente à la fois un pic au moment de la retraite et une augmentation des migrations par la suite, utilise les 13 paramètres et les 5 composantes. Décrite dans des études sur la migration des personnes âgées (Rogers et Watkins 1987), elle est illustrée dans le cadre inférieur droit de la figure 1.

Image

Figure 1 The four main families of the Rogers-Castro model migration schedules showing additive components

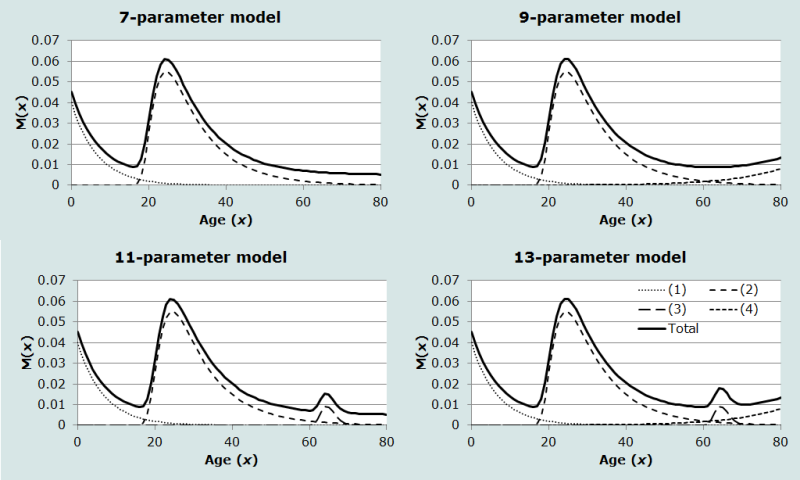
Source : D’après Raymer et Rogers (2008).

Note. Les courbes présentent, en séquence, (1) le schéma de migration par âge des jeunes qui ne sont pas encore sur le marché du travail ; (2) celui des personnes d’âge actif ; (3) celui des personnes retraitées, avec une hausse suivie d’une diminution ; et (4) celui des personnes retraitées avec hausse généralisée aux âges élevés.

Les autres familles de modèles sont des formes restreintes du modèle complet, ce qui signifie qu’au moins une composante en est absente. Par exemple, le schéma le plus courant identifié par Rogers, Little et Raymer (2010) utilise sept paramètres et comporte les deux premières composantes et le terme constant. On l’appelle le schéma standard : son profil est présenté dans le cadre supérieur gauche de la figure 1.

De nombreux schémas de migration présentent le profil standard plus un pic autour de l’âge de la retraite (Rogers et Castro 1981 ; 1986), ce qui équivaut au modèle à 11 paramètres, qui comprend les composantes 1, 2, 3 et 5 (cadre inférieur gauche de la figure 1). Dans les populations qui comptent de nombreux travailleurs migrants, surtout dans les pays en développement, la troisième composante peut donner lieu à un creux au lieu d’un pic, puisque ces immigrés rentrent chez eux au moment de la retraite.

On emploie le modèle à 9 paramètres quand on observe le schéma standard pour les jeunes et les actifs et un redressement de la courbe au-delà de l’âge de la retraite (cadre supérieur droit de la figure 1). Ce cas a été observé dans diverses régions des Pays-Bas en 1974 par Rogers et Castro (1981).

Comme cela devrait être clair d’après ce qui précède, tous les paramètres sont interprétables et peuvent servir à caractériser le modèle auquel ils appartiennent.

Dans la version originale à 11 paramètres du modèle multi-exponentiel de migration, Rogers et Castro (1981) ont illustré leur modèle en l’appliquant aux taux d’émigration interne masculine de Stockholm de 1974. La figure 2 présente les données originales (la courbe irrégulière) et la courbe lisse ajustée à 11 paramètres correspondante.

Cinq des onze paramètres (α₁, α₂, α₃, λ₂ and λ₃) correspondent aux pentes croissantes ou décroissantes des divers segments de la courbe modélisée, tandis que les paramètres de niveau (a₁, a₂, a₃ et c) correspondent aux extremums de la courbe : a₁ pour le pic de la première année de vie, a₂ pour celui des migrations de main-d’œuvre, a₃ pour celui des migrations au moment de la retraite, c étant le taux de migration résiduelle. Les paramètres μ₂ et μ₃ indiquent les âges auxquels interviennent respectivement les pics de migration de main-d’œuvre et de migration de retraités.

Image

Figure 2 The Rogers-Castro 11-parameter model migration schedule fitted to the out-migration rates of males leaving the Stockholm region, 1974

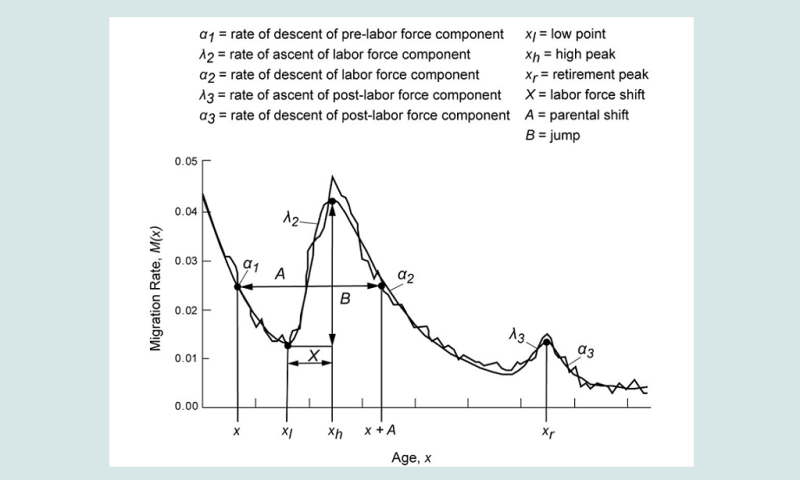
Source : Rogers et Castro (1981). Reproduction autorisée par l’International Institute for Applied Systems Analysis (IIASA).

On peut utiliser divers indices pour décrire soit le schéma observé soit le schéma modélisé. Par exemple, x_l est l’âge auquel la migration est la plus faible avant l’entrée sur le marché du travail, x_h est l’âge auquel elle est la plus forte chez les personnes d’âge actif, et x_r est l’âge du pic de migration au moment de la retraite. On appelle l’écart entre x_l et x_h « labour force shift », X, et la hausse du taux de migration entre x_l et x_h « jump », B. Le « parental shift », A, décrit l’écart d’âge moyen entre la migration des parents et la migration correspondante des enfants. Le taux brut de « migraproduction » (TBM) est le total des taux à tous les âges (c’est-à-dire la surface sous la courbe), et il mesure le niveau global d’émigration interne d’une région, ou le niveau global d’un flux unidirectionnel (d’une région i vers une région j) (Rogers et Castro 1981).

Application de la méthode

L’application de la méthode comporte les étapes suivantes.

Étape 1 : Préparer une série de taux observés

La première étape du calcul d’un modèle de migration consiste à préparer les données. Le choix des indices de migration à utiliser dépend des sources de données disponibles (registre, recensement ou enquête) et de l’objectif de la recherche. Par exemple, dans une étude comparative de schémas migratoires, n’importe quel indice pourrait convenir pourvu qu’il ait été élaboré de la même manière dans les différents contextes à comparer. Par ailleurs, si les modèles doivent servir au calcul de projections de population par année d’âge, le schéma ajusté devrait représenter des taux de migration par année d’âge et année de calendrier. Mais si on ne dispose pas d’observations par année d’âge et année de calendrier qui évoluent de façon relativement lisse en fonction de l’âge, on doit avant tout convertir les données en indices par année d’âge et année de calendrier. Voici plusieurs situations couramment rencontrées.

a.    Données de recensement, taux annuels de migration, période quinquennale           d’observation

Quand un recensement fournit les nombres de migrants survivants au terme d’une période rétrospective de cinq ans ainsi que l’année de la dernière migration, on peut calculer des taux de migration par année de calendrier et année d’âge au moyen d’une procédure, conceptuellement simple mais algébriquement complexe, de rétroprojection décrite par Dorrington et Moultrie (2009). Leur méthode intègre l’effet de la mortalité en appliquant aux migrants le régime de mortalité de la population générale, et l’effet de la migration interrégionale en appliquant les taux annuels de migration de la dernière année pour évaluer la population des régions un an avant le recensement, puis en utilisant ces estimations pour évaluer les taux de migration deux ans avant le recensement et en appliquant ceux-ci pour évaluer la population des régions deux ans avant le recensement, etc. Cela nécessite des données complémentaires sur la région de naissance des enfants de moins de 5 ans et des estimations annuelles de la population des régions par année d’âge. Les schémas de migration ainsi obtenus peuvent être ajustés et lissés par un modèle de Rogers-Castro et être utilisés dans des projections de population année par année.

b.    Interpolation de probabilités annuelles à partir de probabilités                                quinquennales

Quelle que soit la période d’observation des migrations, et que l’on utilise des données de recensement ou de registre, les probabilités de migration sont plus fiables quand elles sont évaluées par groupes quinquennaux que par année d’âge (Rogers, Little et Raymer 2010). En outre, les effectifs de migrants par tranches d’âge d’un an ne sont habituellement disponibles que dans les enquêtes par sondage, car les services statistiques nationaux publient généralement les effectifs de migrants interrégionaux par groupes quinquennaux d’âge.

Pour appliquer le modèle multi-exponentiel quand les indices de migration disponibles se présentent par groupes quinquennaux d’âge, on a besoin d’un procédé de conversion des taux quinquennaux en taux annuels. L’interpolation par spline cubique (McNeil, Trussell et Turner 1977) est l’une de ces techniques, qui fournit une structure par année d’âge lisse. Rogers et Castro (1981) ont utilisé des taux suédois disponibles par année d’âge et par groupes quinquennaux pour tester la précision de cette méthode, et ils ont obtenu des résultats généralement satisfaisants.

Pour obtenir des courbes lisses de migration par année d’âge, les indices de migration observés par groupes quinquennaux d’âge sont attribués à l’âge central de chaque groupe, soit 2 ans, 7 ans, 12 ans, 17 ans, …, 72 ans, 77 ans, etc. (ou 2,5 ans, 7,5 ans, 12,5 ans, …, etc., si on travaille avec des taux plutôt qu’avec des probabilités). À partir de cette série de valeurs, on calcule une série continue de probabilités d’émigration internationale par âge au moyen d’une interpolation par spline cubique qui engendre des polynômes du troisième degré passant par la série des points de contrôle prédéfinis (appelés nœuds). On peut aussi utiliser des extensions, payantes ou libres, de Microsoft Excel, comme XlXtrFun, pour appliquer l’interpolation par spline cubique.

Une approche alternative consiste en une adaptation de la procédure d’interpolation à 6 paramètres de Beers (1945) pour interpoler les taux, des groupes les plus jeunes aux groupes les plus âgés, y compris l’extrapolation à 0 an et 1 an (ou 0,5 an et 1,5 an). Pour cette extrapolation, on suppose que l’écart entre les indices de migration à 1 et 2 ans est le même qu’entre 2 et 3 ans, et que l’écart entre les indices à 0 et 1 an est le même qu’entre 3 et 4 ans.

Donc, quelle que soit l’approche retenue, on a besoin d’une série de taux de migration par groupes quinquennaux d’âge, de 0-4 ans à 65-69 ans au moins.

Étape 2 : Choisir le type de modèle multi-exponentiel

Une fois que la série d’indices observés est prête, on doit choisir le type de modèle multi-exponentiel à adopter. Le système de modèles multi-exponentiels de migration présenté plus haut décrit les caractéristiques des modèles à 7, 9, 11 et 13 paramètres. Ce choix doit se fonder sur un examen visuel de la courbe, en gardant à l’esprit que le modèle est supposé représenter le profil réel de la courbe de migration. Parfois, une fois tracée la représentation graphique, on ne voit pas clairement comment modéliser au mieux la partie correspondant à l’époque de la retraite et aux grands âges. Par exemple, il se peut qu’un modèle classique à 7 ou un modèle à 9 paramètres (migration en hausse aux âges élevés) convienne. Dans une telle situation, le choix en faveur du modèle à 9 paramètres pourrait se fonder sur la perspective théorique d’une hausse de la migration dans les dernières années de la vie. D’un autre côté, le modèle à 9 paramètres pourrait être écarté sur la base des indices de qualité d’ajustement, comme étant insuffisamment économe s’il ne donne pas un meilleur ajustement que le modèle à 7 paramètres. Pour bien choisir le type de modèle, il est recommandé de comparer la qualité d’ajustement d’un modèle simple à celle d’un modèle plus complexe (par exemple, comparer l’ajustement d’un modèle à 7 paramètres à celui d’un modèle à 11 paramètres). En règle générale, et sans perdre de vue la robustesse présumée des données de base, il faut une amélioration sensible de l’ajustement pour justifier le choix d’un modèle plus complexe.

Dans la plupart des pays en développement, en particulier quand l’âge de la « retraite » n’est pas concentré entre 60 et 65 ans et qu’il existe une tendance à exagérer les âges élevés, les données ne sont sans doute pas assez sûres pour s’adapter à un modèle plus complexe que la version à 7 paramètres.

Étape 3 : Ajustement du modèle au moyen du Solveur

Étant donné le nombre de paramètres (entre 7 et 13) des modèles multi-exponentiels de migration, il n’est pas conseillé de déterminer l’ajustement optimal ab initio, par essais et erreurs. Il vaut mieux utiliser des algorithmes analytiques. La procédure que nous présentons ci-dessous utilise un algorithme, Solver, présent dans le logiciel Microsoft Excel. Solver n’est pas toujours fourni dans les configurations habituelles de Microsoft Excel. Pour l’activer, il faut cliquer sur « Fichier→ Options → Compléments → Gérer Compléments Excel → Atteindre … » et s’assurer que la case « Complément solver » est cochée.

Les caractéristiques de la fonction Solver et les conditions et contraintes qu’il faut accepter pour l’employer ont été sélectionnées dans le manuel d’exercices en ligne associé à ce chapitre. Pour appliquer le programme à une feuille de calcul, cliquer sur « Données → Solveur → Résoudre ».

Le modèle ajusté dans le manuel d’exercices en ligne est organisé de manière à permettre à l’utilisateur de décider si la « cible » à minimiser sera la somme des carrés des écarts entre taux observés et taux ajustés ou le chi-carré.

Par défaut, Solver est prévu pour utiliser tous les paramètres. Si on souhaite ajuster une courbe avec seulement quelques-uns des paramètres, on doit le spécifier dans la fenêtre « Cellules variables » et attribuer aux autres paramètres des valeurs fixes pertinentes (qui peuvent être ou non égales à zéro, selon les exigences de la procédure d’ajustement). Nous présentons ci-dessous un exemple dans lequel une telle optimisation sous contrainte peut être nécessaire.

La somme des carrés des écarts se calcule ainsi :

$$\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left(O_i-F_i\right)}^2}$$

où O_i représente le taux observé à l’âge i, F_i la valeur ajustée à l’âge i et n le nombre de groupes d’âge.

Le chi-carré se calcule ainsi :

$$\frac{1}{n}{\displaystyle \sum _{i=1}^n\frac{{\left(O_i-F_i\right)}^2}{F_i}}.$$

Le chi-carré est plus sensible aux mauvais ajustements aux âges où les taux sont faibles (ce qui engendre une erreur proportionnellement plus importante), et il constitue donc un meilleur indicateur de la qualité d’ajustement quand on tente d’ajuster la « bosse de la retraite » (la troisième composante).

Le choix des valeurs initiales de la procédure d’ajustement

Le choix des valeurs de départ est la principale difficulté dans l’estimation de paramètres non-linéaires. Dans l’idéal, à partir d’un ensemble de valeurs initiales, l’algorithme procède par itérations et débouche sur une série corrigée de valeurs « optimales ». Mais cet optimum peut n’être qu’un optimum local et non général. Un meilleur choix des valeurs des paramètres de départ peut entraîner une qualité d’ajustement améliorée et aboutir à une série différente de valeurs finales. Un choix moins pertinent de valeurs initiales peut empêcher toute convergence, même vers un optimum local.

Gardant ceci à l’esprit, la méthode la plus efficace pour s’assurer que les résultats d’une procédure d’ajustement seront réellement « optimaux » est de choisir des valeurs des paramètres utilisées antérieurement pour une courbe « similaire ». À cet effet, on peut commencer avec les valeurs déjà introduites dans le manuel d’exercices en ligne, qui ont servi à ajuster les courbes dans les exemples développés ci-dessous.

La convergence peut être plus difficile à atteindre avec les modèles à 11 et 13 paramètres. Quand le recours à ces modèles plus lourds est justifié, on peut essayer d’ajuster d’abord aux données un modèle classique à 7 paramètres (ce qui assure déjà l’ajustement pour le pic de la courbe et pour les âges de la première moitié de la vie). Puis on peut figer ces 7 paramètres à la valeur obtenue lors de cette première étape (et donc les traiter à partir de là comme des constantes) et ensuite évaluer les paramètres restants. Une autre procédure efficace consiste à appliquer d’abord une méthode d’estimation linéaire, qui ne comporte pas d’algorithme itératif. Cette méthode a été décrite pour la première fois par Rogers et Castro (1981) et incluse ensuite dans la série de techniques alternatives présentée par Rogers, Castro et Lea (2005).

La recherche d’une solution optimale comporte un autre défi : le choix d’un critère d’arrêt de l’algorithme itératif. Quand la procédure itérative converge vers une solution, le chi-carré, qui mesure les écarts entre valeurs observées et valeurs estimées, diminue. On a atteint une solution acceptable quand le chi-carré ne diminue plus que d’une quantité négligeable entre une itération et la suivante. La valeur de cette faible variation, appelée « seuil de tolérance », est définie par l’utilisateur. On peut être tenté de la fixer à un niveau très bas, donc très proche de zéro, pour aller jusqu’à une valeur véritablement minimale du chi-carré. Mais le risque de cette attitude est qu’un seuil de tolérance aussi bas ne soit jamais atteint, même quand une solution a été obtenue. Press, Flannery, Teukolsky et al. (1986) proposent 0,001 comme valeur raisonnable du seuil de tolérance. Si le programme ne converge pas, on peut alléger les critères de convergence, en relevant le seuil de tolérance ou en essayant une nouvelle série de valeurs de départ.

Pour le choix des valeurs de départ, une autre méthode, procédant par essais et erreurs, s’appuie sur les graphiques du manuel d’exercices Excel associé à ce chapitre (en ligne). En introduisant votre propre série de données observées dans l’une des feuilles de calcul, vous pouvez formuler des « hypothèses initiales » sur les valeurs des paramètres et les introduire dans les cellules destinées à leurs valeurs finales. Ensuite, après examen visuel de l’ajustement obtenu et identification des paramètres les moins satisfaisants, relancez la procédure avec de nouvelles valeurs de ceux-ci. Continuez ainsi jusqu’à ce que la courbe ajustée soit raisonnablement proche de la courbe observée. Vous aurez alors en main des valeurs initiales acceptables à introduire dans la procédure d’estimation non-linéaire par les moindres carrés.

Étape 4 : Évaluer la qualité d’ajustement du modèle

On évalue la qualité d’ajustement du modèle en calculant l’écart absolu moyen en pourcentage (EAMP ; en anglais : mean absolute percent error) :

$$EAMP=100\frac{1}{n}{\displaystyle \sum }_{i=1}^n\left[\frac{|F_i-O_i|}{O_i}\right].$$

L’EAMP a tendance à exagérer les erreurs, surtout quand les données observées comportent de nombreuses valeurs proches de zéro (Morrison, Bryan et Swanson 2004).

En plus de l’EAMP, on calcule également le R², le carré du coefficient de corrélation entre les valeurs des O_i et celles des F_i. À titre heuristique, on considère couramment qu’un ajustement raisonnable est atteint avec un EAMP inférieur ou égal à 15 % et un R² sensiblement supérieur à 90 %.

Par ailleurs, puisque la méthode suppose que le modèle de Rogers-Castro calculé représente l’allure réelle de la courbe de migration, il devrait représenter la structure sous-jacente des données observées.

Étape 5 : Interprétation des résultats de l’ajustement

Si l’objectif est de décrire le schéma de migration et si on a pu ajuster un modèle multi-exponentiel aux données, on peut utiliser n’importe quel indice résumé (par exemple le taux brut de migration, X, B ou A), ainsi que les estimations des paramètres, pour caractériser la série. Les indices résumés et les interprétations des paramètres sont donnés dans la présentation générale, plus haut dans ce chapitre.

Exemples

Dans les exemples développés ci-dessous, on applique des modèles multi-exponentiels de migration à diverses séries de données, de qualité et de complexité variable, provenant de différentes sources. Tous ces exemples sont fournis dans le manuel d’exercices en ligne sur le site web Tools for Demographic Estimation.

C’est parce qu’on doit recourir à des méthodes itératives pour ajuster une table-type de mortalité aux probabilités conditionnelles de survie aux âges adultes que les exemples ne sont pas développés en détail dans le texte. Nous renvoyons le lecteur à l’explication, fournie dans la section précédente, de l’utilisation de Solver, dans Microsoft Excel, pour déterminer les ajustements optimaux. Le manuel d’exercices est prêt à employer Solver pour le calcul des résultats présentés.

Données de recensement, migrations sur une période d’un an

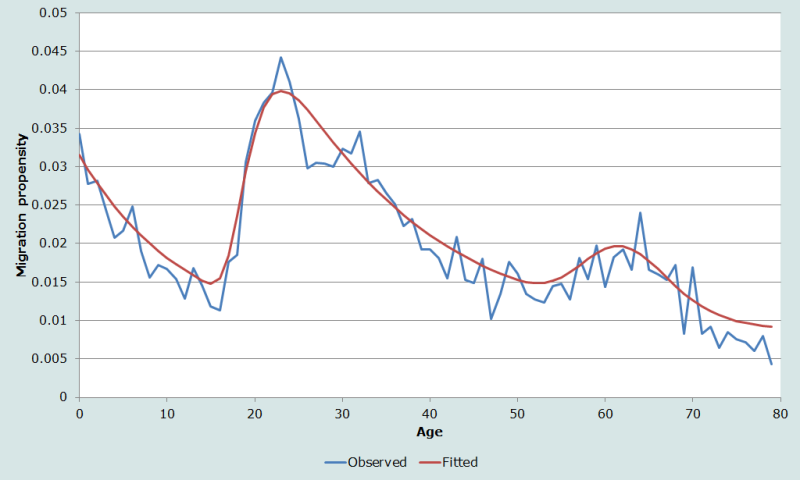
La figure 3 présente un exemple basé sur des probabilités de migration par année d’âge sur une période d’un an, à partir des données d’un recensement. Les données proviennent de l’American Community Survey (ACS) de 2005, une enquête nationale réalisée chaque année par le US Census Bureau. Même dans le cas de la Californie, un État fortement peuplé, les probabilités de migration par année d’âge sur une période d’un an sont très instables. L’EAMP est égal à 17 % et le R² à 0,92.

Il faut être prudent quand on utilise des probabilités de migration par année d’âge sur des périodes d’un an. Pour chaque année d’âge, les effectifs soumis au risque de migration et les effectifs de migrants peuvent être faibles, et cela engendre des probabilités irrégulières et instables. Il peut être préférable de calculer des probabilités par groupes quinquennaux d’âge, qui s’avèrent plus fiables que les probabilités par année d’âge (Rogers, Little et Raymer 2010), et calculer ensuite par interpolation les probabilités par année d’âge, soit par spline cubique, soit par la formule de Beer, comme on l’a vu dans la section consacrée à l’application de la méthode.

Image

Figure 3 Out-migration over the 1-year interval, 2004-2005, with fitted 11-parameter model schedule, California, 2005 American Community Survey

Données de recensement, migrations sur une période de cinq ans

L’exemple de la figure 4 utilise des données de recensement relatives à l’État du New Hampshire. L’échantillon public de données individuelles (PUMS) à 1 % du US Bureau of Census est un échantillon relativement petit extrait du recensement, et le New Hampshire est l’un des États les moins peuplés. Les probabilités de migration par année d’âge sont très instables, leurs fluctuations sont énormes, mais le modèle donne une estimation lissée du véritable profil de la courbe. L’EAMP est égal à 52 % et R² à 0,68.

Image

Figure 4 Out-migration over the 5-year interval, 1995-2000, and fitted with a 7-parameter model schedule, New Hampshire, 2000 Census 1 per cent PUMS

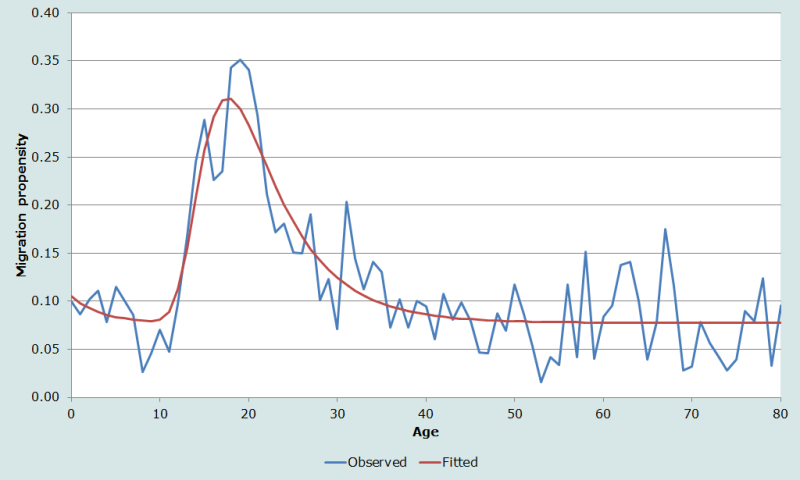
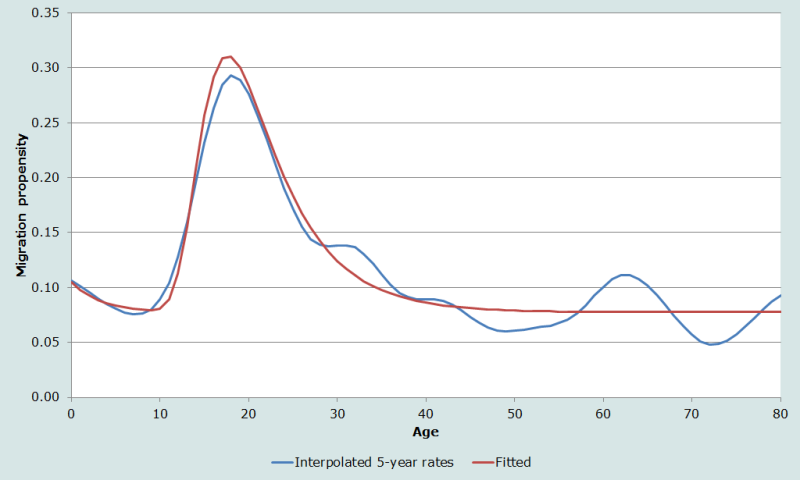
La figure 5 présente l’application de la méthode d’interpolation des splines cubiques aux probabilités de migration par groupes quinquennaux d’âge du New Hampshire, calculées à partir des données de l’échantillon public à 1 % du recensement de 2000. La courbe des valeurs interpolées à partir des taux quinquennaux est nettement plus lisse et donne des estimations plus fiables que la courbe des valeurs observées par année d’âge de la figure 4, elle constitue donc une meilleure série d’estimations à comparer avec la courbe ajustée multi-exponentielle. L’EAMP, qui valait 52 % avec les probabilités par année d’âge, tombe à 15 % avec les valeurs interpolées à partir des probabilités par groupes quinquennaux d’âge, et R² passe de 0,68 à 0,94.

Plusieurs facteurs expliquent pourquoi les niveaux des probabilités de migration sont nettement plus élevés au New Hampshire (figure 5) qu’en Californie (figure 3). L’exemple californien présente les migrations sur une période d’un an et l’exemple du New Hampshire porte sur une période de cinq ans. De plus, le territoire du New Hampshire est beaucoup plus petit que celui de la Californie, et on s’attend généralement à ce que la migration soit d’autant plus intense que la zone géographique est plus petite.

Image

Figure 5 Out-migration over the 5-year interval, 1995-2000, and fitted with a 7-parameter model schedule, New Hampshire, 2000 Census 1 per cent PUMS. (Migration rates in 5-year age groups and interpolated)

Diagnostics, analyse et interprétation

Contrôles et validation

Il est important de vérifier par examen visuel si les taux de migration par âge ont un profil compatible avec les modèles de Rogers-Castro. Si ce n’est pas le cas, il est probable que ces modèles ne donneront pas un ajustement satisfaisant. De même, il vaut la peine de contrôler l’existence de valeurs extrêmes, en particulier pour les âges élevés, ce qui pourrait fausser le choix des paramètres ou même le choix du nombre de paramètres à prendre en compte pour l’ajustement. Si les données observées sont particulièrement erratiques, il est bon de les regrouper par classes quinquennales d’âge et de calculer ensuite une distribution lissée en utilisant soit l’interpolation à 6 paramètres de Beer soit une courbe spline.

Remarques sur l’application de la méthode

La théorie du modèle multi-exponentiel a été présentée plus haut dans ce chapitre, nous ne la répéterons pas ici. Dans cette section, nous développerons en détail certains éléments à examiner attentivement avant toute mise en application de la méthode.

Préparation des données

Le modèle multi-exponentiel s’applique à des séries de taux de migration par année d’âge, généralement de 0 an jusqu’à 65 ans, voire au-delà de 65 ans pour couvrir pleinement le schéma de migration des personnes âgées. Les données de migration par âge peuvent concerner un flux unidirectionnel (c’est-à-dire d’une région i vers une région j) ou l’émigration interne totale (c’est-à-dire d’une région i vers toutes les autres régions), ou l’ensemble des migrations interrégionales sans distinction d’origine ou de destination. Habituellement, les données sur les migrations proviennent des recensements nationaux (ou, dans les pays développés, des registres de population). Le modèle multi-exponentiel peut s’appliquer à divers indices de migration par année d’âge calculés à partir de l’une quelconque de ces sources.

Quand il est calculé à partir des données d’un registre national, le taux de migration des personnes qui avaient l’âge x au début d’une période déterminée est le rapport du nombre de migrations observées au cours de cette période au nombre moyen de personnes-années exposées au risque de migration. Certaines personnes peuvent migrer plus d’une fois en cours de période. Ce sont des taux du type événements/exposition au risque, bien que les migrations de personnes qui n’ont pas survécu jusqu’à la fin de la période puissent ne pas figurer au numérateur (Rogers et Castro 1981).

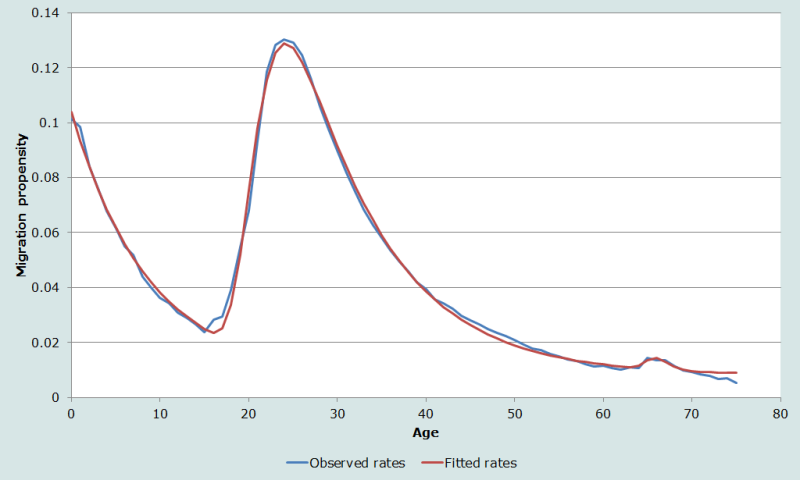
Les données de la courbe de migration de la figure 2, sur l’émigration masculine de Stockholm sur une période d’un an, provenaient du registre national suédois. Par contre, la figure 6 présente les séries observée et estimée par le modèle de l’ensemble des migrations masculines intercommunales suédoises sur une période de cinq ans. Comme il fallait s’y attendre, les niveaux sont beaucoup plus élevés sur la figure 6, du fait que les migrations sont plus intenses quand toutes les régions sont envisagées que quand il s’agit seulement de la région de Stockholm. On s’attend également à observer davantage de migrations sur une période de cinq ans que sur une seule année. Rees (1977) a constaté que les probabilités de migration sur cinq ans sont généralement moins que cinq fois (entre trois et cinq fois) supérieurs à la probabilité sur un an. La courbe des taux observés est aussi plus lisse et plus proche de celle du modèle sur la figure 6, ce qui signifie que les taux par année d’âge sont plus fiables quand ils sont mesurés sur une longue période.

Image

Figure 6 Swedish male inter-communal migration over the 5-year interval, 1968-1973 with fitted 11-parameter model schedule

D’un autre côté, les recensements dénombrent les migrants survivants (et non les migrations). Les migrants sont les personnes qui déclarent résider dans une région au début de la période rétrospective considérée et dans une autre région au moment du recensement. Une personne qui a fait plusieurs migrations, consignées dans le registre national, peut être considérée comme non-migrante lors du recensement si elle est revenue à son point de départ. En général, les effectifs de migrants dénombrés par un recensement sont inférieurs aux nombres de migrations, surtout quand la période d’observation est longue et permet donc qu’il y ait de nombreux retours et de nombreux migrants décédés. C’est pourquoi une série de mesures de la migration fondée sur le registre de population n’est pas directement comparable à une série basée sur un recensement (Rogers et Castro 1986).

Habituellement, les recensements enregistrent la résidence actuelle de chaque individu et lui demandent où il résidait un an ou cinq ans auparavant. Avec ces données et l’âge des individus au moment du recensement, on établit les nombres de migrants survivants et de survivants qui étaient exposés au risque de migration. Le rapport du nombre de migrants survivants au nombre de survivants exposés au risque de migrer est parfois qualifié de « conditionnel », parce que tant les migrants que les personnes exposées au risque de migration doivent avoir survécu jusqu’à la fin de la période rétrospective considérée pour être comptabilisés par le recensement (Rogers, Little et Raymer 2010). Comme ce n’est pas un taux du type événements/exposition au risque, nous parlerons plutôt ici de probabilité de migrer.

Données de recensement, migrations sur une période d’un an

Pour calculer des probabilités de migration par année d’âge quand le recensement demande à chaque personne où elle vivait un an auparavant, toutes les personnes sont « renvoyées » à la région où elles habitaient un an plus tôt quand elles avaient un an de moins, ce qui nous donne le nombre de personnes soumises au risque de migrer au départ de cette région. Par exemple, un enfant d’1 an au recensement de 2010 avait 0 an en 2009. Si les âges en 2010 vont de 1 à 85 ans, ceux de 2009 vont de 0 à 84 ans. (Note : seules les personnes âgées d’1 an et plus auront déclaré un lieu de résidence un an auparavant.) Revenir un an en arrière donne le nombre de personnes qui, ayant survécu jusqu’au recensement de 2010, étaient exposées au risque d’émigrer de la région i en 2009. Le nombre d’émigrants est celui des personnes qui ont déclaré habiter la région i en 2009 et ont été recensées dans une autre région en 2010. Pour chaque année d’âge, le rapport du nombre de migrants au nombre de personnes exposées au risque de migrer donne la probabilité d’émigration interne par âge sur l’année précédant le recensement. Quand le numérateur est un nombre de migrants unidirectionnels, c’est-à-dire de personnes qui ont migré de la région i vers la région j, ce rapport constitue la probabilité de migrer de la région i vers la région j, par âge.

Il faut être prudent quand on utilise des probabilités de migration par année d’âge sur une période d’un an. Pour chaque année d’âge, les effectifs soumis au risque de migration et les effectifs de migrants peuvent être faibles, et cela engendre des probabilités irrégulières et instables. Il peut être préférable de calculer des probabilités par groupes quinquennaux d’âge, qui s’avèrent plus fiables que les probabilités par année d’âge (Rogers, Little et Raymer 2010), et calculer ensuite par interpolation les probabilités par année d’âge.

Données de recensement, migrations sur une période de cinq ans

Si le recensement demande à chaque individu où il habitait cinq ans auparavant, on peut calculer des probabilités de migrer par année d’âge sur la période de cinq ans tant que l’âge de chacun est connu. Pour ce faire, on « renvoie » tous les individus à la région où ils vivaient cinq ans avant, quand ils avaient cinq ans de moins. Les enfants âgés de 5 ans lors d’un recensement effectué en 2000, par exemple, avaient 0 an en 1995. Si les âges en 2000 vont de 5 à 85 ans, ceux de 1995 vont de 0 à 80 ans. Le nombre d’émigrants est celui des personnes qui ont déclaré habiter la région i en 1995 et ont été recensées dans une autre région en 2000. Pour chaque année d’âge, le rapport du nombre de migrants au nombre de personnes exposées au risque de migrer donne la probabilité d’émigration interne par âge sur les cinq années précédant le recensement.

Données de recensement, taux annuels de migration sur une période de cinq ans

Quand le recensement donne les nombres de migrants qui ont survécu jusqu’au terme d’une période de cinq ans, on peut calculer des taux de migration par année d’âge et année de calendrier au moyen d’une procédure de rétroprojection décrite par Dorrington et Moultrie (2009). Cette méthode intègre l’effet de la mortalité en appliquant aux migrants le régime de mortalité de la population générale, et l’effet des migrations répétées en appliquant les taux annuels de migration de la dernière année pour évaluer la population des régions un an avant le recensement, puis en utilisant ces estimations pour évaluer les taux de migration deux ans avant le recensement et en appliquant ceux-ci pour évaluer la population des régions deux ans avant le recensement, etc. Cela nécessite des données complémentaires sur la région de naissance des enfants de moins de 5 ans et des estimations annuelles de la population des régions par année d’âge. Les schémas de migration ainsi obtenus peuvent être ajustés et lissés par un modèle de Rogers-Castro et être utilisés dans des projections de population année par année.

Limites

À moins que l’on ait des données exactes ne présentant aucune irrégularité, le modèle multi-exponentiel ne fournit pas d’ajustement très précis et peut donc être surparamétré, en ce sens que plusieurs séries différentes de paramètres peuvent s’ajuster aussi bien les unes que les autres aux données observées. En pareil cas, il pourrait être utile de donner une valeur constante à un ou deux paramètres et de procéder à l’ajustement avec les autres ; nous recommandons donc une certaine modération quant au nombre de paramètres.

Extensions de la méthode

L’application du modèle multi-exponentiel ne se limite pas aux séries de taux ou probabilités de migration. Plusieurs études ont montré que les structures par âge de migrants (et de migrations si on dispose de données de registre) ont souvent une forme multi-exponentielle et peuvent être fidèlement représentées par un modèle de Rogers-Castro (Little et Rogers 2007 ; Rogers, Little et Raymer 2010).

On peut déterminer les nombres de migrants ou de migrations par année d’âge en utilisant l’une ou l’autre des sources de données et des méthodes présentées plus haut, car ce sont simplement les numérateurs des taux ou probabilités de migration. Les données observées ajustées par les modèles sont les rapports des nombres de migrants ou de migrations par année d’âge à leurs totaux respectifs. (Note : si les effectifs de migrants sont distribués par classes quinquennales d’âge, l’un ou l’autre type d’interpolation sera nécessaire ; si on utilise l’interpolation par spline cubique, l’effectif associé à chaque centre de classe doit être l’effectif de la classe quinquennale divisé par cinq.)

Par exemple, la figure 7 présente la distribution de fréquences des migrations suédoises par âge. Elle se révèle très lisse et fiable, à l’exception des âges les plus élevés. Un modèle à 7 paramètres donne un très bon ajustement, avec un R² de 0,99 et un EAMP de 29 %. Mais cet exemple montre comment l’EAMP peut exagérer l’imperfection du modèle, car il « gonfle » excessivement en présence d’une série de petites variations dans les données observées.

Image

Figure 7 Swedish age composition of inter-communal migration, 1968-1973 and fitted with a 7-parameter model schedule

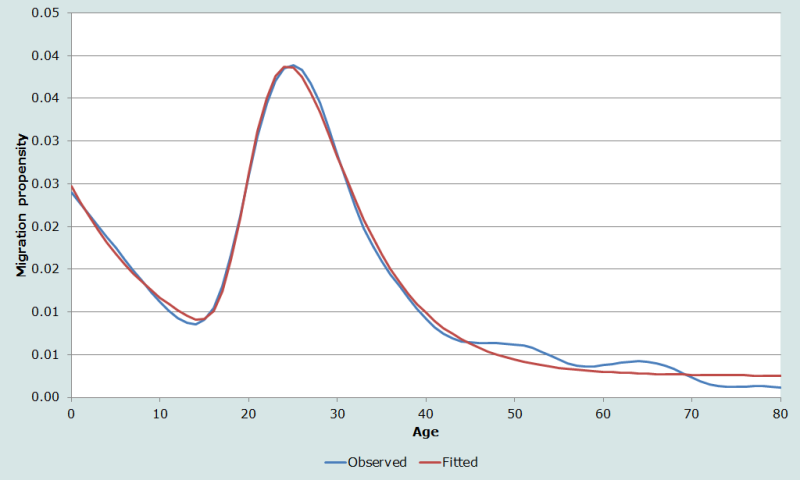
Il existe deux autres logiciels qui permettent d’ajuster la courbe multi-exponentielle en Excel dans le manuel d’exercices. Ce sont : (1) Data Master 2003, un programme gratuit d’ajustement de courbes qui applique l’algorithme de Levenberg-Marquardt ; et (2) R (R Core Team), un environnement logiciel, gratuit également, destiné aux calculs statistiques et représentations graphiques en tous genres, et qui demande donc un temps d’apprentissage assez long avant de pouvoir être utilisé en toute sécurité. L’Appendice à ce chapitre, sur le site web Tools for Demographic Estimation, fournit des instructions élémentaires pour la définition des fonctions de R nécessaires au calcul des modèles à 7 et 11 paramètres en utilisant l’algorithme de Gauss-Newton.

Références

Bates J and I Bracken. 1982. "Estimation of migration profiles in England and Wales", Environment and Planning A 14(7):889-900. doi: https://dx.doi.org/10.1068/a140889

Bates J and I Bracken. 1987. "Migration age profiles for local-authority areas in England, 1971-1981", Environment and Planning A 19(4):521-535. doi: https://dx.doi.org/10.1068/a190521

Beers H. 1945. "Six-term formulas for routine actuarial interpolation", The Record of the American Institute of Actuaries 33(2):245-260.

Dorrington R and TA Moultrie. 2009. "Making use of the consistency of patterns to estimate age-specific rates of interprovincial migration in South Africa," Paper presented at Annual Meeting of the Population Association of America. Detroit, Michigan, 29 April - 2 May 2009.

George MV. 1994. Population projections for Canada, provinces and territories, 1993-2016. Ottawa: Statistics Canada, Demography Division, Population Projections Section.

Hofmeyr BE. 1988. "Application of a mathematical model to South African migration data, 1975–1980", Southern African Journal of Demography 2(1):24–28.

Kawabe H. 1990. Migration rates by age group and migration patterns: Application of Rogers' migration schedule model to Japan, The Republic of Korea, and Thailand. Tokyo: Institute of Developing Economies.

Liaw K-L and DN Nagnur. 1985. "Characterization of metropolitan and nonmetropolitan outmigration schedules of the Canadian population system, 1971-1976", Canadian Studies in Population 12(1):81-102.

Little JS and A Rogers. 2007. "What can the age composition of a population tell us about the age composition of its out-migrants?", Population, Space and Place 13(1):23-19. doi: https://dx.doi.org/10.1002/psp.440

McNeil DR, TJ Trussell and JC Turner. 1977. "Spline interpolation of demographic data", Demography 14(2):245-252. doi: https://dx.doi.org/10.2307/2060581

Morrison PA, TM Bryan and DA Swanson. 2004. "Internal migration and short-distance mobility," in Siegel, JS and DA Swanson (eds). The Methods and Materials of Demography. San Diego: Elsevier pp. 493-521.

Potrykowska A. 1988. "Age patterns and model migration schedules in Poland", Geographia Polonica 54:63-80.

Press WH, BP Flannery, SA Teukolsky and WT Vetterling. 1986. Numerical Recipes: The Art of Scientific Computing. Cambridge: Cambridge University Press.

R Core Team (2012). R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/

Raymer J and A Rogers. 2008. "Applying model migration schedules to represent age-specific migration flows," in Raymer, J and F Willekens (eds). International Migration in Europe: Data, Models and Estimates. Chichester: Wiley, pp. 175-192.

Rees PH. 1977. "The measurement of migration, from census data and other sources", Environment and Planning A 9(3):247-272. doi: https://dx.doi.org/10.1068/a090247

Rogers A and LJ Castro. 1981. Model Migration Schedules. Laxenburg, Austria: International Institute for Applied Systems Analysis. https://pure.iiasa.ac.at/id/eprint/1543/1/RR-81-030.pdf

Rogers A and LJ Castro. 1986. "Migration," in Rogers, A and F Willekens (eds). Migration and Settlement: A Multiregional Comparative Study. Dordrecht: D. Reidel, pp. 157-208.

Rogers A, LJ Castro and M Lea. 2005. "Model migration schedules: Three alternative linear parameter estimation methods", Mathematical Population Studies 12(1):17-38. doi: https://dx.doi.org/10.1080/08898480590902145

Rogers A and JS Little. 1994. "Parameterizing age patterns of demographic rates with the multiexponential model schedule", Mathematical Population Studies 4(3):175-195. doi: https://dx.doi.org/10.1080/08898489409525372

Rogers A, JS Little and J Raymer. 2010. The Indirect Estimation of Migration: Methods for Dealing with Irregular, Inadequate, and Missing Data. Dordrecht: Springer.

Rogers A and J Raymer. 1999. "Estimating the regional migration patterns of the foreign-born population in the United States: 1950-1990", Mathematical Population Studies 7(3):181-216. doi: https://dx.doi.org/10.1080/08898489909525457

Rogers A and J Watkins. 1987. "General versus elderly interstate migration and population redistribution in the United States", Research on Aging 9(4):483-529. doi: https://dx.doi.org/10.1177/0164027587094002