Estimation de la mortalité adulte à partir de la survie des frères et sœurs
Description de la méthode
Cette méthode calcule la mortalité adulte directement à partir de données fournies par les adultes sur leurs fratries (c’est-à-dire, leurs frères et sœurs). Elle ne peut être appliquée que si une enquête a recueilli des histoires de fratries complètes. Ces histoires sont obtenues en demandant à chaque répondant le nom, le sexe, l'âge, le statut de survie et, s’ils sont décédés, l'âge et l'année du décès de chacun de ses frères et sœurs nés de la même mère. Les informations sur les frères sont utilisées pour estimer la mortalité des hommes et les informations sur les sœurs pour estimer la mortalité des femmes. Plusieurs enquêtes recueillent les histoires de fratries uniquement à partir des informations fournies par les femmes ; mais les histoires de fratries collectées auprès des répondants de sexe masculin peuvent être analysées en utilisant exactement les mêmes méthodes. Comme les répondants et leurs frères et sœurs ont en moyenne le même âge, les informations sur les fratries des répondants peuvent être utilisées pour mesurer la mortalité dans les mêmes groupes d'âge que ceux des répondants.
La collecte des histoires de fratries est un processus complexe qui nécessite une formation et une supervision rigoureuses du personnel de terrain pour être exécutée correctement. Ce n’est pas une méthode de collecte dont l’utilisation est appropriée dans un recensement. De nombreuses Enquêtes Démographiques et de Santé (EDS) collectent des histoires de fratries (le terme utilisé dans les EDS est le «Module mortalité maternelle»). Alors que la plupart de ces enquêtes ont recueilli ces informations seulement auprès des femmes âgées de 15 à 49 ans, car c’est pour ces femmes qu’est complété le questionnaire individuel détaillé, certaines EDS ont aussi collecté de la même façon des histoires de fratries auprès des hommes.
Un avantage que les méthodes basées sur la fratrie ont sur les questions relatives au décès survenu dans les ménages est que seuls les recensements ou exceptionnellement les grandes enquêtes peuvent collecter des informations sur un nombre relativement important de décès survenus dans les ménages au cours de l'année précédant l'enquête pour produire des estimations de mortalité qui soient suffisamment précises pour être utiles. Parce que les répondants donnent en moyenne des informations sur plusieurs frères et sœurs, et qu’on peut calculer des taux sur plusieurs années d'exposition, les estimations peuvent être faites à partir d’histoires de fratries collectées dans de plus petites enquêtes. Néanmoins, toutes les méthodes permettant d’estimer la mortalité des adultes nécessitent que soient collectées des données sur plusieurs milliers de ménages. Un autre avantage de la méthode est qu’elle repose sur une procédure d'estimation dans lequel peu d’hypothèses interviennent, en particulier, elle ne suppose pas que la population étudiée soit fermée à la migration. Les résultats ne seront toutefois pas représentatifs concernant des petits états ou des régions dans lesquels une proportion substantielle de la population aura émigré ou sera composée d’immigrés.
Contexte
Les méthodes d’origine élaborées pour estimer la mortalité à partir des informations sur la survie des frères et sœurs étaient des méthodes indirectes fondées sur l'idée que l'âge moyen des frères et sœurs des répondants de tout âge est proche de l'âge de ces répondants. La proportion des frères et sœurs encore en vie d'un répondant est donc un bon estimateur de la probabilité de survivre (dans une table de mortalité) jusqu’à l'âge du répondant (Hill and Trussell 1977 ; Division de la Population des NU 1984). Malheureusement, sur le terrain, l'application de cette approche a montré que la qualité des données recueillies sur les frères et sœurs était souvent assez pauvre, parce que les frères ou les sœurs qui décèdent avant ou peu après la naissance du répondant sont souvent omis par les répondants qui peuvent tout ignorer d’eux (Blacker and Brass 1983 ; Zaba 1986).
L'intérêt pour l'estimation de la mortalité à partir des données sur les fratries a été relancé par le développement de la méthode des sœurs pour mesurer la mortalité maternelle (Graham, Brass and Snow 1989). Cette méthode suppose que l’on dispose de données sur le nombre de sœurs du répondant qui ont survécu jusqu’à l'âge de 15 ans, le nombre d'entre elles qui sont décédées par la suite, et parmi les sœurs décédées, le nombre de celles qui étaient enceintes au moment du décès, ou qui étaient enceintes dans les 6 à 8 semaines qui ont précédé le décès. En limitant l’analyse aux frères et sœurs à qui ont survécu jusqu’à l’âge de 15 ans, on exclut de fait les frères et sœurs qui sont décédés avant 15 ans et, par conséquent, peuvent avoir été ignorés ou oubliés par la répondant. Les réponses fournies par les répondantes aux deux premières questions dans chaque groupe d'âge quinquennal permettent de calculer les proportions de sœurs encore en vie parmi celles qui ont survécu à 15 ans. La méthode indirecte de la survie des frères et sœurs adultes a ensuite été développée pour estimer la mortalité des femmes adultes toutes causes confondues à partir des mêmes proportions des femmes encore en vie. Des données comparables sur les frères des répondants peuvent être utilisées pour estimer la mortalité des hommes.
La méthode permettant d’estimer directement la mortalité adulte à partir des informations sur l’histoire des fratries a été lancée par le programme d’Enquêtes Démographiques et de Santé (EDS), en s’inspirant des recherches antérieures détaillées plus haut (Rutenberg and Sullivan 1991). Cette technique est plus ambitieuse en termes de quantité d'information qui est recueillie auprès des répondants ; elle est également plus demandeuse du point de vue des répondants et du personnel de terrain qui mène les interviews. Cependant, en remplaçant les estimations indirectes fondées sur des modèles démographiques par des mesures directes des taux de mortalité des adultes, on réduit le nombre d'hypothèses nécessaires pour produire ces estimations, et de façon plus importante encore, on peut ainsi distinguer les décès survenus dans un passé récent et les décès survenus plus loin dans le passé, qui sont connus pour être rapportés avec moins de précision.
Données nécessaires et hypothèses
Tabulation de données nécessaires
Le calcul direct des taux de mortalité à partir des histoires de fratries implique a peu près les mêmes démarches que le processus plus familier de calcul des taux de mortalité infanto-juvénile à partir des données d'histoires génésiques. En effet, une histoire complète des frères et sœurs du répondant, quand elles incluent le répondant, est en fait une histoire génésique de leur mère. Cependant, en comparaison avec les estimations de mortalité faites pour les enfants, les estimations de mortalité adulte sont entachées d’importantes erreurs d'échantillonnage. Cela reflète le fait que les taux de mortalité sont beaucoup plus bas à l'âge adulte que dans l'enfance et que, dans une population en croissance, le nombre de frères et sœurs exposés aux risques de mortalité est plus petit que le nombre d'enfants déclarés par les mères. Par conséquent, dans toutes les enquêtes auprès des ménages, on observe beaucoup moins de décès parmi les frères et sœurs adultes que parmi les enfants.
Le calcul des mesures de mortalité qui se réfèreraient à des cohortes à partir d’histoires de frères et sœurs a peu d’intérêt au vu de la facilité avec laquelle les logiciels modernes d'exploitation et d’analyse de données d'enquêtes permettent de calculer les durées d'exposition au risque de décès. Ainsi, ce document met l'accent sur le calcul des taux de mortalité par âge et par période à partir des données sur l’histoire des fratries et sur la façon avec laquelle on peut en déduire d'autres indicateurs de mortalité.
Pour calculer la mortalité des femmes, on a besoin des données suivantes :
- Le nombre de décès des sœurs des répondants selon la période et le groupe quinquennal d'âge des sœurs au moment de leur décès.
- Le nombre d’années d'exposition vécues par les sœurs et distribuées par période et par groupe quinquennal d'âge de ces sœurs (au moment de l'exposition au risque).
Pour calculer le taux de mortalité des hommes, on a besoin des données suivantes :
- Le nombre de décès des frères des répondants selon la période et le groupe quinquennal d'âge des frères au moment de leur décès.
- Le nombre d’années d'exposition vécues par les frères et distribuées par période et par groupe quinquennal d'âge de ces frères (au moment de l'exposition au risque).
Le calcul des durées d'exposition doit généralement exclure le répondant lui-même ou la répondante elle-même (par définition, ceci est fait quand on analyse les données sur les sœurs récoltés par les hommes et vice versa). Cette condition est expliquée dans la discussion sur les hypothèses importantes formulées pour cette méthode.
Les tableaux sur la fratrie de même sexe que le répondant (c'est-à-dire les sœurs des femmes et les frères des hommes) doivent être pondérés seulement par les pondérations d’échantillonnage fournies avec les données. Les tableaux sur la fratrie de sexe opposé (c'est-à-dire les frères des femmes et les sœurs des hommes) doivent en outre être pondérés par l’inverse de la taille de la fratrie survivante de même sexe que le répondant. Cette nécessité sera aussi expliquée dans la discussion sur les hypothèses importantes faites par la méthode.
La période de temps pendant laquelle l'exposition au risque de mortalité est mesurée peut être définie en termes de dates du calendrier ou par rapport à la date à laquelle le répondant a été interviewé. Cette dernière approche permet une utilisation optimale des données, car elle garantit assure que le temps vécu par les fratries des répondants au cours des années incomplètes dans lequel les entretiens ont eu lieu est tout de même inclus dans l’analyse. Alternativement, le calcul des taux de mortalité sur des années civiles particulières a l'avantage de donner des résultats qui correspondent à un temps précis et comparable avec celui associé aux estimations provenant d'autres sources. Cette approche implique généralement de ne pas prendre en compte les données de l'année où l’enquête a eu lieu sur le terrain (bien qu’on puisse choisir d’inclure ces données dans la période la plus récente si le plus gros des interviews a eu lieu à la fin de cette année).
Le fichier Excel associé à ce chapitre est conçu pour calculer les taux de mortalité pour deux périodes successives antérieures à la date de la collecte des données sur le terrain. Beaucoup de rapports d’EDS fournissent des taux pour la période de sept ans précédant l’enquête (soit, 0-6 années complètes) et une façon d’utiliser ce fichier Excel serait de calculer les taux de mortalité pour les trois années précédant l'enquête et ensuite pour les quatre années qui précèdent ces trois années. Alternativement, on pourrait calculer les taux de mortalité pour deux périodes de quatre ans et donc pour une période totale de huit ans précédant la collecte des données sur les histoires des fratries. L'expérience montre que l'exhaustivité de la déclaration des frères et sœurs décédés et la précision avec laquelle leurs âges et leurs dates de décès sont déclarés se dégradent souvent rapidement pour des événements survenus loin dans le passé. En outre, en utilisant des périodes de quatre ans plutôt que de cinq ans, on minimise les erreurs qui résultent de l'attribution par erreur de dates de décès à cinq et dix ans avant la collecte des données en raison d’une tendance à arrondir les années.
Les groupes d'âge de frères et sœurs pour lesquels les données sont collectées doivent correspondre globalement à l'âge des répondants qui ont procuré les informations. Par exemple, afin de mesurer la mortalité entre 15 et 60 ans, dans les meilleures de cas, les données sur la survie de frères et sœurs devraient être recueillies auprès des répondants âgés de 15 à 59 ans. Si les données sont collectées uniquement auprès d’adultes, peu d'entre eux ont des frères et sœurs qui sont encore de jeunes enfants, et, même si les données sur les enfants ne sont pas biaisées par l’omission de certains frères et sœurs décédés, les estimations sont susceptibles d'être entourées par d’importantes erreurs d'échantillonnage et elles ne seront pas représentatives de tous les jeunes enfants. Ainsi, pour les EDS et les autres enquêtes qui recueillent des données sur les histoires de fratries auprès de répondants âgés de 15 à 49 ans, l'indice de mortalité préféré est 35q15, c’est-à-dire la probabilité qu’un individu âgé de 15 ans décède avant d’atteindre son 50e anniversaire.
Bien que la probabilité conditionnelle de décéder entre 15 et 60 ans (45q15) soit largement utilisée par les agences internationales et d'autres organisations comme indice de prédilection de mortalité des adultes, le nombre de décès déclarés par les répondants âgés de 15 à 49 pour la tranche d'âge 55-59 ans sera plus faible que celui rapporté pour les groupes d'âge plus jeunes. Ainsi, plutôt que de calculer directement 45q15, il est préférable de le faire en ajustant une table de mortalité standard aux estimations obtenues pour les âges de 15 à 54 ans, puis en extrapolant à partir de ce modèle pour obtenir la mortalité dans la dernière classe d'âge de cinq ans. C’est l’approche qui est mise en œuvre dans le fichier Excel associé.
Pour éliminer les ambiguïtés résultant des mariages polygames et des remariages, il est généralement indiqué aux enquêteurs que la ‘fratrie’ concerne les enfants nés de la même mère. Que cela ait été fait ou non, les réponses peuvent généralement être acceptées telles qu’elles sont. Aussi longtemps que les répondants ont le même groupe de parents à l’esprit quand ils listent les frères et sœurs en vie, d’une part, et d’autre part, ceux sont décédés, il importe peu pour l’estimation de la mortalité de savoir exactement qui sont les parents des frères et sœurs.
Si les histoires de fratries ont été recueillies auprès des hommes et des femmes, leurs réponses devraient généralement être exploitées séparément de sorte que les deux ensembles de données puissent être pondérés de manière appropriée et qu’il soit possible de vérifier la cohérence de l’une série par rapport à l’autre.
Hypothèses importantes
Une limitation inhérente aux méthodes de mesure de la mortalité adulte fondées sur les fratries est qu’elles sous-estiment la mortalité dans la mesure où cette mortalité se concentre au sein de certaines fratries (c'est-à-dire au sein de certains ensembles de frères et/ou de sœurs nés de la même mère). Cette concentration (clustering en anglais) survient chaque fois que les décès sont plus concentrés dans une petite fraction des fratries que sous le seul effet du hasard et elle résulte de l’hétérogénéité entre fratries face au risque de décès des individus (Zaba and David 1996). Il en résulte un biais vers le bas des estimations de mortalité, simplement parce que les membres des fratries à forte mortalité sont moins nombreux que les membres de fratries à faible mortalité à survivre pour répondre aux questions sur leurs frères et sœurs. Ce biais ne peut pas être complètement corrigé car, à la limite, les fratries dont les membres sont tous décédés ne sont déclarées par personne. Il n’est pas possible de savoir combien de ces fratries ont existé ou quelles étaient leurs tailles, bien qu’il soit possible de faire des suppositions à leur égard.
Les schémas par âge estimés et les tendances de la mortalité seront biaisées si l’effet de clustering de la mortalité au sein des fratries varie avec l'âge. En effet, si les caractéristiques partagées par les frères et sœurs (par exemple, les facteurs génétiques, les premières expériences de la vie, le statut socio-économique, les styles de vie, et le lieu de résidence) influencent fortement la mortalité des adultes d'âge moyen, alors que la mortalité avant 40 ans a une grande composante aléatoire, les estimations de mortalité pour les adultes plus âgés seront davantage sous-estimées que celles faites pour les jeunes adultes.
La question du biais résultant des réponses multiples aux questions sur les fratries a donné lieu à une abondante littérature. Le problème existe aussi bien dans les données d’enquêtes que de recensements, car plus un individu est cité dans un recensement, plus il a de chances d’avoir un frère ou une sœur qui le cite dans un échantillon probabiliste.i En outre, même dans les enquêtes, il peut arriver que des réponses multiples soient données concernant un même individu. Par exemple, si deux sœurs de la même mère sont interrogées dans le même ménage, il y aura des déclarations multiples concernant les autres membres de leur fratrie. La procédure d’analyse standard utilisée, par exemple, dans les rapports EDS s’appuie sur les événements et les durées d’exposition des frères et sœurs cités, en laissant de côté la durée d’exposition de la répondante (survivante) elle-même. Les événements et la durée d’exposition sont pondérés seulement par les pondérations d’échantillonnage du répondant, sans prendre en compte les nombres de répondants survivants potentiels dans la fratrie.
Trussell et Rodriguez (1990) ont démontré mathématiquement que, pour des fratries dont tous les membres font face à un risque identique de décéder, le calcul standard qui exclut aussi le répondant du dénominateur des mesures donne des estimations non biaisées de la mortalité. En effet, la réduction – au numérateur - du nombre de mentions d’un frère ou d’une sœur décédés, du fait que les personnes décédées ne peuvent pas se citer l’une l’autre, et l’exclusion des répondants vivants du dénominateur se compensent mutuellement et donnent le risque correct concernant chaque fratrie en tant que groupe.
La question des biais qui pourraient résulter de différences de mortalité en fonction de la taille de la fratrie est liée à la question de la déclaration multiple de certains frères ou sœurs. Elle a suscité beaucoup d’intérêt chez les chercheurs car, à la différence d’autres facteurs qui jouent sur le risque au sein des fratries classées par sexe et âge du répondant, la taille de la fratrie de chaque répondant est connue. Si la mortalité ne varie pas avec la taille de la fratrie, les estimations standard sont les mêmes à la fois pour chaque taille de fratrie, y compris les fratries d’une personne qui sont exclues de l’analyse parce que le répondant n’a personne à déclarer, et pour la population dans son ensemble. Même si la mortalité varie avec la taille de la fratrie, les estimations standard restent sans biais pour chaque taille de la fratrie, comme l’a montré Masquelier (2013). Mais pour obtenir des estimations de la mortalité pour la population, il convient de repondérer les estimations relatives aux fratries de différentes tailles en fonction de la distribution des tailles des fratries observée dans la population. Quand les répondants citent les personnes de même sexe, on peut le faire en divisant la proportion de frères ou sœurs dans les fratries survivantes de même taille par la fréquence des fratries de cette taille dans la population. Pour les fratries d’une seule personne, leur mortalité doit être extrapolée à partir de la mortalité dans les fratries de plus grandes tailles.
Gakidou et King (2006) soutiennent que, à l’inverse de la démarche standard, les fratries doivent inclure le répondant survivant, mais elles doivent toujours être pondérées en plus par la probabilité qu’elles soient déclarées – c’est-à-dire par l’inverse du nombre de répondants potentiels qui survivent dans la fratrie. Comme dans la démarche de Masquelier, un ajustement supplémentaire doit aussi être fait pour les fratries non déclarées du fait du décès de tous leurs membres. Dans une analyse des histoires complètes de fratries tirées d’enquêtes EDS, Obermeyer, Rajaratnam, Park et al. (2010) estiment que l’absence d’ajustement pour tenir compte des chances variables d’être mentionné par plusieurs frères et sœurs peut biaiser de -20 % les estimations de la mortalité toutes causes confondues.
Toutefois, Masquelier (2013) soutient que Obermeyer et al. ont repondéré les données de façon inappropriée et qu’il en est résulté une surestimation du biais. Il souligne que, si on doit repondérer, il importe d’ajuster seulement pour tenir compte de la chance d’être mentionné plusieurs fois, mais uniquement par les frères et sœurs qui ont survécu à l’âge initial à partir duquel la mortalité est mesurée. Mais il s’interroge en outre sur la réalité de la variation de la mortalité par taille de la fratrie. Il pourrait s’agir d’un artefact dû à l’omission plus fréquente des frères et sœurs décédés dans les histoires relatives à des fratries de plus grandes tailles. C’est pourquoi Masquelier recommande d’utiliser l’approche standard, sans essayer de repondérer les données relatives à chaque taille de fratrie. A partir de là, soit la mortalité est estimée pour chaque taille de la fratrie, et une estimation repondérée est obtenue pour la population de la même façon que l’approche décrite dans les précédents paragraphes, soit les estimations ne font l’objet d’aucune pondération supplémentaire. Comme il est nécessaire, pour obtenir des estimations séparées pour chaque taille de fratrie, que l’on dispose d’un très large échantillon ou que l’on utilise des modèles de régression pour ajuster les données, c’est la seconde approche (l’absence de pondération spécifique pour les tailles de fratries) qui est retenue ici.
La problématique est différente quand on analyse les déclarations qui portent sur le sexe opposé (par exemple, les réponses faites par des femmes au sujet de leurs frères). Dans ce cas, le répondant ne fait pas partie du groupe exposé au risque de décéder. Toutefois, le calcul standard donnera encore des résultats biaisés pour l’ensemble de la population si la mortalité des frères est associée au nombre de sœurs, dans l’exemple où c’est l’une d’entre elles qui est interrogée. Concernant les déclarations qui portent sur le sexe opposé, il est donc clair qu’il faut pondérer chaque déclaration par l’inverse du nombre de frères ou sœurs du même sexe que le répondant, comme suggéré par Gakidou et King (2006). Bien entendu, les questions sur les membres de la fratrie de sexe opposé ne peuvent évidemment donner aucune information sur les fratries au sein desquelles aucun membre survivant n’est de même sexe que le répondant. L’adoption de cette démarche revient donc à supposer que la mortalité des individus dans de telles fratries est égale à la mortalité du reste de la population. Mais dans les enquêtes qui recueillent des données auprès des deux sexes, chacun d’entre eux fournit cette information sur l’autre, de sorte qu’on peut pondérer les décès et l’exposition au risque déclarés par les répondants par l’inverse de la probabilité que les frères et sœurs dans chaque groupe d’âge soient mentionnés.
Travaux préparatoires et recherches préliminaires
La première étape dans l'analyse des données sur l’historique des fratries devrait consister à évaluer l'ampleur de la non-déclaration et de l’incomplétude des informations dans l'ensemble de données, en particulier le nombre de répondants qui ont déclaré qu'ils ne savaient pas si une sœur ou un frère particulier était encore en vie ou ont simplement omis de répondre à la question. Il est également important d'évaluer la qualité de données sur les dates naissance des frères et sœurs et de vérifier si, l'âge à l’enquête ou leur âge au décès sont manquants ou ont été imputés. Si beaucoup de répondants n’ont pas répondu à ces questions, les données observées peuvent ne pas être représentatives de la population dans son ensemble. En plus, un niveau élevé de non-réponse peut indiquer que le personnel de terrain ou les répondants ont eu quelques difficultés avec les questions ; il peut être éclairant de déterminer si ces problèmes sont observés chez une minorité des enquêteurs ou au sein d’une catégorie spécifique de répondants. Une concentration des âges ou des années sur certains chiffres particuliers reflète également une mauvaise qualité de l’information recueillie. Si les données sur l'âge et les dates semblent être de mauvaise qualité, on peut potentiellement obtenir de meilleurs résultats en analysant les données avec la méthode indirecte relative à la survie des frères et des sœurs à l’âge adulte.
Si les femmes et les hommes ont été interrogés, un moyen utile de vérifier l'exhaustivité des données est d'évaluer combien de frères et sœurs sont rapportées en moyenne par les répondants du sexe opposé et si le rapport de masculinité à la naissance change nettement à mesure que l'âge du répondant ou l’intervalle de temps depuis la naissance du frère ou de la sœur augmente. Il est assez fréquent d’observer que les enquêtés d’un des deux genres (généralement des hommes) rapporte moins de frères et sœurs, et en particulier moins de frères et sœurs décédés. Dans d'autres enquêtes, les hommes et les femmes peuvent déclarer un même nombre de frères et sœurs de chaque sexe (après avoir ajusté les données pour tenir compte du fait que les répondants ne renseignent pas sur eux-mêmes), mais des nombres différents de frères et sœurs qui sont survivants. Le premier type d’écarts pourrait résulter de déclarations d'âge erronées, ce qui n’est pas le cas du second type d’incohérences.
Tout biais associé à l’effet de clustering de la mortalité au sein de certaines familles résulte se traduit par une sous-estimation. En outre, il semble peu probable que les répondants inventent les frères et sœurs qui n’existent pas ou déclarent que leurs frères et sœurs vivants sont décédés. Ainsi, l'analyse devrait probablement se concentrer sur les données fournies par les répondants du sexe qui renseignent le plus de frères et sœurs et la plus grande proportion de frères et sœurs décédés.
Précautions et mises en garde
- Les seules méthodes faisant usage de données sur les fratries qui peuvent être recommandées produisent des probabilités de survie au-delà de 15 ans, conditionnées au fait d'avoir au moins survécu à 15 ans exacts. En théorie, il est possible de collecter et d'analyser des données sur les décès de frères et sœurs quand ils sont encore des enfants. Malheureusement, ces données sont souvent très incomplètes, en particulier pour les frères et sœurs qui sont décédés avant ou peu après la naissance du répondant. Ainsi, la plupart des applications de la méthode cherchent uniquement à mesurer la mortalité des frères et sœurs à 15 ans ou plus. Pour produire une table de mortalité complète, il faut estimer des probabilités de survie de la naissance à 15 ans en faisant recours à d’autres sources de données.
- Même dans une grande enquête, le nombre de frères et sœurs qui décèdent chaque année dans chaque groupe d'âge reste faible. Dans la plupart des applications de la méthode, les décès et la période d'exposition doivent être regroupés sur plusieurs années afin d'estimer des taux de mortalité qui sont assez précis pour être utiles. Ainsi, la méthode est peu susceptible d'être utile pour détecter des variations brusques ou des fluctuations rapides de la mortalité chez les adultes.
- A mesure que l’on exploite les données en remontant dans le temps avant la période de collecte, le nombre de frères et sœurs exposés au risque de décéder diminue rapidement, en particulier aux âges élevés. En outre, les répondants ont tendance à omettre certains frères et sœurs décédés, en particulier les décès qui sont survenus dans un passé lointain. Ainsi, les histoires de fratrie conduisent généralement à sous-estimer la mortalité et ce biais s’aggrave pour les estimations qui sont éloignées de la période de collecte. Ainsi, la méthode directe relative aux frères et sœurs ne devrait pas être utilisée pour estimer les taux de mortalité pour une période éloignée de plus de 10 ans de l’enquête. Souvent, seules les données portant sur les sept dernières années sont analysées.
- Étant donné que la probabilité d’omission des frères et sœurs décédés augmente à mesure que l’intervalle de temps écoulé depuis leurs décès et l’enquête s’agrandit, le calcul des taux de mortalité pour deux périodes précédant l'enquête sert surtout à un examen de la plausibilité des estimations. Il permet à l’analyste de vérifier si les données indiquent une augmentation invraisemblable de la mortalité. Il faut être prudent avant d’extrapoler les tendances de la mortalité adulte à partir des estimations faites à partir d’un seul ensemble de données sur la fratrie.
- La procédure directe d’estimation de la mortalité adulte à partir de l’information sur les frères et sœurs adultes n’implique pas l’hypothèse d’une population fermée à la migration. Il peut néanmoins être difficile d’interpréter des estimations fondées sur la fratrie concernant la mortalité d’unités géographiques infranationales, comme des zones urbaines et rurales ou des districts, ou des groupes de répondants ayant des caractéristiques socioéconomiques spécifiques. En effet, si les frères et sœurs partagent généralement la même identité ethnique, il arrive fréquemment que les frères et sœurs vivent ailleurs que les répondants et aient des caractéristiques socioéconomiques différentes d’eux. Les estimations relatives aux populations infranationales risquent aussi d’avoir de très larges intervalles de confiance.
Application de la méthode
Que l'on analyse les données sur les frères, les sœurs, ou les deux sexes combinés, et que l’on utilise les informations procurées par les hommes, les femmes ou les deux sexes, la procédure d'estimation des taux de mortalité à partir des histoires de fratries est la même. Le fichier Excel est conçu pour calculer les taux de mortalité pour les frères et pour les sœurs pour deux périodes précédant une enquête et pour l'ensemble de la période couverte par la combinaison de ces deux périodes. Des feuilles de calcul séparées sont fournies pour l'analyse des données fournies par les hommes et les femmes enquêtées. Le classeur peut produire des estimations pour des périodes de durée variable et pour les données exploitées par année avant l'enquête ou pour des années calendrier qui correspondent globalement à ces années avant l’enquête.
Deux tabulations sont nécessaires pour calculer les taux de mortalité pour les frères et sœurs de chaque sexe à partir des informations fournies par les répondants de chaque sexe, donnant potentiellement lieu à quatre paires de tabulations. Un tableau croisé devrait porter sur le nombre de décès de frères et sœurs par âge pour chaque année civile et un autre tableau devrait concerner les personnes-années d’exposition au risque de décès par âge pour chaque année civile. On peut produire les données pour les groupes d'âge et les périodes qui vont être utilisées dans l'analyse. Alternativement, on peut produire les tableaux par année d'âge et par année calendrier de sorte que les données sur les décès et les personnes-années puissent être ensuite agrégées dans un ensemble d'intervalles plus larges jugées pertinentes.
Comme on peut supposer que les dates de naissance ou de décès de certains frères et sœurs n’auront pas été déclarées, la manière la plus satisfaisante pour corriger ce problème dans les données consiste à imputer des dates exactes à l’aide de nombres aléatoires afin d’attribuer à un frère ou à une sœur une date exacte à laquelle l'événement a pu se produire (Stanton, Abderrahim and Hill 1997). Les organismes qui ont conduit les enquêtes, tels que MeasureDHS, ont peut-être procédé à de telles imputations avant de diffuser les données provenant des enquêtes qu’elles ont réalisées.
Pour que l’imputation et l’analyse des données portant sur certains frères et sœurs soient possibles, on a besoin de connaître soit leur date de naissance ou leur âge actuel s’ils sont en vie, ainsi que leur année de décès, leur âge au décès ou le temps écoulé en année depuis leur décès s’ils sont décédés. Si les deux dates de naissance et de décès sont toutes deux incomplètes, on peut généralement attribuer au hasard à la personne une date exacte de naissance avant de lui assigner une date de décès précise. Des précautions doivent être prises pour enregistrer la clé (appelée seed en anglais) utilisée pour générer des nombres aléatoires, de sorte que les dates imputées puissent être reproduites exactement si on a besoin de recréer les fichiers de données utilisées pour estimer les taux de mortalité à partir des données originales.
Les détails de la procédure qui devrait être utilisée pour procéder à l'imputation des dates exactes dépendent des questions précises posées aux répondants notamment sur les âges et les dates de décès de leurs frères et sœurs. Quelques exemples suffiront pour illustrer les principes des calculs. Si le répondant a été interviewé le 23/11/2011 et a indiqué que l'un de ses frères et sœurs était âgé de 33 ans, la date de naissance de cette personne doit se situer entre le 24/11/1977 et le 23/11/1978. Si un frère est né en octobre 1972 et décédé à 17 ans, il faudrait d'abord lui attribuer au hasard une date exacte de naissance, peut-être le 14/10/1972, puis lui attribuer une date exacte de décès entre le 14/10/1989 et le 13/10/1990. Si le répondant a donné une information sur l’année de décès de son frère, la période dans laquelle on choisit au hasard une date de décès devrait être limitée à l'année correcte en question.
Il faut s’assurer que la date de décès qui a été assignée à partir d’un nombre d’années écoulées depuis la naissance du frère ou de la sœur décédé n’excède pas la date de l’interview du répondant. Par exemple, si le répondant a été interviewé le 28/2/2003 et a déclaré que son frère est né en 1980 et décédé à 23 ans, alors on considérera que cette personne est née dans les deux premiers mois de 1980 et que son décès a eu lieu en 2003, mais, au plus tard le 28 février 2003. La procédure d'imputation doit également veiller à ce que les dates de naissance imputées se produisent dans un ordre temporel correct.
Une fois qu’une date exacte de naissance a été attribuée à chaque frère et sœur et, qu’une date exacte de décès a été assignée à ceux qui sont décédés, il est facile d'identifier les groupes d'âge où les décès se sont produits et de repartir les durées vécues par chaque personne entre les groupes d’âge et les périodes d’exposition (Stanton, Abderrahim and Hill 1997). Les logiciels modernes d'analyse de données d'enquêtes contiennent souvent des commandes qui font ce calcul de façon semi-automatisée.
Graphiquement, la mortalité est mesurée pour le groupe d'âge et la période de temps définie par les lignes épaisses dans la figure 1. Le parcours de vie d'un individu est représenté par âge et période par les lignes diagonales (telles qu’il le serait dans un diagramme de Lexis classique). Le groupe d'âge pour lequel la mortalité est calculée est défini par un intervalle ayant xl comme limite inférieure, et xh comme limite supérieure. La période de temps pendant laquelle la mortalité est calculée est (t2 - t1), où t2 est la date de fin de la période et t1 la date du début de la période. Ainsi, toutes les personnes d’âge x au temps t1 qui ne décèdent pas avant t2 seront âgées de xt2 = xt1 + (t2 - t1) au temps t2. Pour les statistiques sur la mortalité des adultes, l'âge et les périodes de temps sont presque toujours mesurés en années.
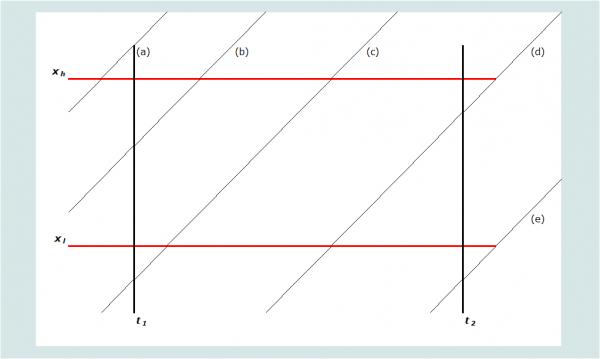
Il convient de noter que la durée d'exposition vécue par chaque frère ou sœur dans une année donnée est presque toujours divisée entre deux âges adjacents. Cinq scénarios possibles sont représentés sur la figure 1, marqué de (a) à (e). En notant xd l'âge au décès des personnes qui décèdent dans un groupe d'âge donné et une période donnée, le calcul pour chaque scénario des personnes-années d'exposition vécues par les frères et sœurs des répondants dans ce groupe d'âge et cette période peut être fait à partir des formules reprises dans le tableau 1. En additionnant les durées d’exposition de l'ensemble des frères et sœurs, on obtient le dénominateur pour le taux de mortalité, soit le total d’années d'exposition au risque dans le groupe d'âge au cours de la période. La somme de décès survenus dans la même tranche d'âge et la même période fournit le numérateur du taux.
Tableau 1 Algorithme pour déterminer la durée d’exposition au risque de mortalité
|
Scénario |
Description |
Règles définissant la durée d’exposition |
Période d’exposition vécue par les survivants |
Période d’exposition des décédés (si le décès a lieu dans la période) |
|
(a) |
Plus âgé que xh à t1 |
xt1 > xh |
0 |
0 |
|
(b) |
Age entre xl et xh à t1. Atteint l’âge xh dans la période |
xl < xt1 < xh xt1+(t2-t1) > xh |
xh-xt1 |
xd-xt1 |
|
(c) |
Atteint xl et xh dans la période |
xl > xt1 xt1+(t2-t1) > xh |
xh-xl |
xd-xl |
|
(d) |
Atteint xl dans la période. La période se termine avant xh |
xl > xt1 xl < xt1+(t2-t1) < xh |
xt1+(t2-t1) > xl |
xd-xl |
|
(e) |
N’atteint pas xl dans la période |
xt1+(t2-t1) < xl |
0 |
0 |
Une fois que les tabulations des décès et des durées d'exposition ont été produites, diverses mesures de mortalité peuvent être générées en utilisant les formules standards de construction d’une table de mortalité. Dans la feuille de calcul Excel, ces calculs sont effectués pour les données présentées par groupes quinquennaux d'âge. Le taux de mortalité par âge, 5Mx, est obtenu en divisant les décès dans un groupe d'âge quinquennal au cours d’une année spécifique (ou d’un ensemble d’années) par les personnes-années d’exposition au risque de mortalité dans ce groupe et durant cette période :
La probabilité de décéder dans un groupe d'âge quinquennal, 5qx peut être calculée pour les années concernées à partir du taux de mortalité correspondant à l'aide de la formule standard, qui suppose que les décès sont répartis uniformément à l’intérieur du groupe d'âge :
La probabilité de survie dans un groupe d'âge quinquennal, 5px, est 1 – 5qx.
A partir de la série d'estimations de 5px, on peut calculer la probabilité cumulée de décéder entre 15 ans et 50 ans pour la période (35q15), en multipliant les probabilités intermédiaires de survie dans les intervalles de cinq ans pour obtenir la probabilité de survie de 15 à 50 (35q15), et en soustrayant cette probabilité de 1 pour obtenir son complément :
Les intervalles de confiance à 95 pour cent qui entourent ces mesures synthétiques de la mortalité des adultes sont calculées dans la feuille de calcul en utilisant la formule de Greenwood. Cette formule suppose que les données sont générées à partir d'un échantillon aléatoire simple et surestiment ainsi la précision des indicateurs basés sur des données provenant d'enquêtes par grappes.
La feuille de calcul fournit une représentation graphique des logits des probabilités conditionnelles de survie de 15 ans à chacun des âges ultérieurs, rapportés aux valeurs équivalentes des logits des survivants d’une table type de mortalité. Ces diagrammes sont utiles pour évaluer la qualité des estimations. Les erreurs de données apparaissent habituellement sous la forme d’irrégularités dans la série ou sur la forme d’une courbe qui fléchit vers le bas dans les groupes d’âge les plus élevés. Ce dernier trait est caractéristique d’une sous-estimation de la mortalité due à l'exagération des âges à l’enquête et des âges au décès.
Enfin, la feuille de calcul ajuste un modèle relationnel à 2-paramètre associé à une table type de mortalité sur la série de valeurs np15 au moyen d'une régression linéaire simple sur tous les groupes d'âge de 15 à 55 ans. Ceci va atténuer l’ampleur de certaines erreurs dans la série. Les valeurs ajustées des probabilités 35q15 et 45q15 sont extraites de cette table de mortalité ajustée. La feuille de calcul peut calculer ces indicateurs de mortalité en utilisant soit le modèle Général des tables types des Nations Unies (UN Population Division 1982) ou l'une des quatre familles des tables types de mortalité de Princeton (Coale, Demeny and Vaughan 1983). La table type de mortalité choisie devrait avoir une structure par âge de la mortalité au sein des âges adultes qui ressemble à celle de la population étudiée. Une autre table de mortalité peut être utilisée comme standard s’il y a de bonnes raisons de penser qu'elle se rapproche davantage de la structure de la mortalité des adultes dans la population étudiée. La table de mortalité la plus appropriée peut ne pas appartenir à la famille de modèles qui saisit le mieux la relation entre la mortalité des enfants et celle des adultes. Si on ne sait rien de la structure par âge de la mortalité à l'âge adulte, l'utilisation du modèle général des Nations Unies ou du modèle Ouest de Princeton est recommandée.
Exemple
Les calculs à la base de la méthode sont illustrés dans le tableau 2 à l'aide des données sur la survie des sœurs recueillies auprès des femmes interrogées dans l'enquête sur la mortalité maternelle du Bangladesh (Maternal Mortality Survey of Bangladesh 2001), disponible sur le site de DHS. Cette enquête menée au Bangladesh disposait d’un échantillon exceptionnellement large. Les décès et les durées d'exposition des sœurs des répondantes appartenant aux différents groupes d'âge quinquennaux ont été cumulés sur la période de sept ans précédant l'enquête. Après le calcul des taux et des probabilités de survie de la table de mortalité, ces dernières ont été lissées par ajustement d’une table type de mortalité à l’aide d’un modèle relationnel à 2-paramètres et en utilisant le modèle Sud des tables de mortalité de Princeton comme standard.
Tableau 2 Calcul direct des taux de mortalité des femmes par âge et des quotients de mortalité entre 15 et 50 ans ainsi que 15 et 60 ans, Bangladesh, 1994-2001
|
Groupe d’âge x à x+4 |
Décès des sœurs
|
Personnes-années d’exposition
|
Taux de mortalité 5Mx |
Probabilité de décéder sur cinq ans 5px |
Probabilité cumulée de décéder x-10p15 |
Logits x-10Y15 |
Logits ajustés x-10Y15 |
|
15-19 |
350,3 |
211 840,6 |
0,00165 |
0,9918 |
0,9918 |
-2,3956 |
-2,4318 |
|
20-24 |
436,8 |
241 208,5 |
0,00181 |
0,9910 |
0,9828 |
-2,0235 |
-2,0109 |
|
25-29 |
488,0 |
241 111,4 |
0,00202 |
0,9899 |
0,9729 |
-1,7909 |
-1,7758 |
|
30-34 |
455,0 |
210 963,3 |
0,00216 |
0,9893 |
0,9625 |
-1,6225 |
-1,5978 |
|
35-39 |
417,5 |
160 378,1 |
0,00260 |
0,9871 |
0,9500 |
-1,4727 |
-1,4472 |
|
40-44 |
377,5 |
97 268,6 |
0,00388 |
0,9808 |
0,9318 |
-1,3072 |
-1,3020 |
|
45-49 |
242,0 |
50 456,1 |
0,00480 |
0,9763 |
0,9097 |
-1,1550 |
-1,1581 |
|
50-54 |
169,4 |
19 621,2 |
0,00863 |
0,9577 |
0,8713 |
-0,9561 |
-1,0002 |
|
55-59 |
56,7 |
6 276,6 |
0,00904 |
0,9558 |
0,8328 |
-0,8027 |
-0,8286 |
|
35q15 (95% CI) |
|
0,090 |
(0,086 - 0,094) |
(α = |
-0,191) |
0,090 |
|
|
45q15 (95% CI) |
|
0,167 |
(0,155 - 0,179) |
(β = |
0,949) |
0,160 |
|
La figure 2 présente les estimations en vis-à-vis du standard de mortalité, en distinguant les périodes entre 0 à 2 ans et entre 3 à 6 ans avant l'enquête. Les estimations équivalentes pour les frères des répondants sont présentées dans la figure 3. Pour ces données particulières, les estimations ajustées de 35q15 et 45q15 sont presque identiques aux estimations calculées directement à partir des données observées soit 90 pour 1000 et 167 pour 1000 respectivement.
Diagnostics, évaluation et interprétation
Contrôles et validation
Si des histoires de fratries ont été recueillis à la fois auprès des hommes et des femmes dans un recensement ou dans une enquête de grande envergure, il est recommandé de les analyser séparément par sexe des répondants, afin d’évaluer la cohérence de leurs déclarations. La mortalité des individus d'un sexe déterminé, tel que rapporté par leurs frères, devrait être le même que la mortalité des mêmes individus tels que rapportés par leurs sœurs. Le cas contraire laisserait supposer la présence d’un biais important dans les estimations pour un ou pour les deux sexes. La cohérence dans les données collectées ne garantit bien sûr pas leur exactitude, mais des différences statistiquement significatives entre les estimations obtenues à partir des répondants d’un des deux sexes pris séparément signifient qu'au moins un des deux sexes, et peut-être les deux, a donné des réponses inexactes aux questions. Ce type de contrôle sur les résultats ne pourrait pas être effectué sur les données de l'enquête sur la mortalité maternelle au Bangladesh 2001, car les histoires de fratries n’ont été recueillies qu’auprès des femmes dans cette étude.
Interprétation
Les résultats de l'application de la méthode directe de calcul des taux de mortalité à partir des histoires de fratries collectées dans l'enquête sur la mortalité maternelle au Bangladesh en 2001 sont présentés dans les figures 2 et 3. Ils sont encourageants. Les points relevés ne sont pas erratiques et la courbe ne fléchit pas vers le bas aux âges plus élevés. Il y a une certaine courbure dans la série masculine, en particulier pour la période antérieure, mais ceci couvre toute la série de données de 20 ans jusqu'à 60 ans, et ne concerne pas uniquement les âges plus élevés. Ceci indique probablement que la structure par âge de la mortalité dans cette population diffère de celle de la table-type de mortalité qui a été utilisée.
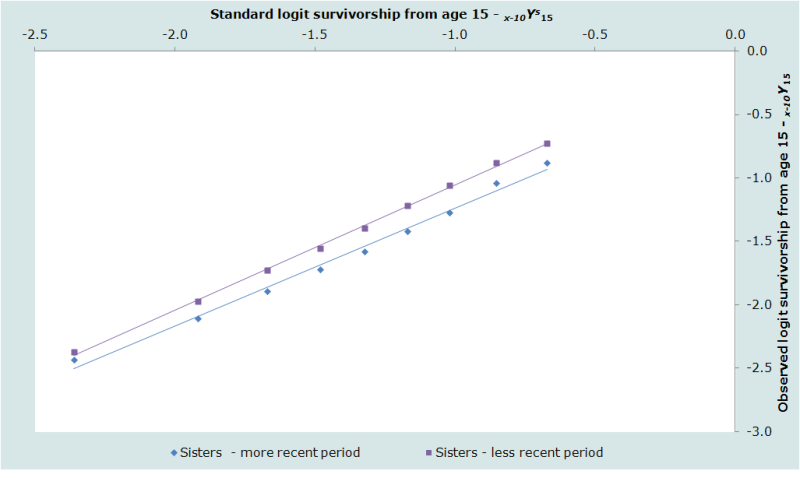
Les estimations relatives aux deux périodes sont cohérentes l’une par rapport à l’autre pour les deux sexes, suggérant que la mortalité adulte a baissé de façon substantielle dans les années 1990. Ainsi, on estime que la probabilité de décéder entre 15 et 50 ans pour les hommes a chuté de 104 pour 1000 à 76 pour 1000 entre la période située de 3 à 6 ans avant l’enquête et la période située de 0 à 2 ans avant l’enquête. La probabilité de décéder entre 35 et 50 ans a chuté chez les femmes de 107 pour mille à 73 pour mille au cours de ces deux mêmes périodes.

Bien que la probabilité globale de décéder entre 15 et 50 ans au Bangladesh soit très similaire pour les hommes et les femmes et ait diminué presque au même rythme pour les deux sexes, les figures 2 et 3 révèlent que les structures par âge de la mortalité aux âges adultes des hommes et des femmes sont très différentes dans ce pays. La mortalité augmente beaucoup plus fortement avec l'âge pour les hommes que pour les femmes. Le paramètre β de table de mortalité féminine modèle ajustée aux données de 1994 à 2001 est de 0,95 tandis qu’il est de 1,14 pour les hommes. Ainsi, si l'on examine les taux de mortalité pour les groupes d'âge quinquennaux, ils montrent qu’au Bangladesh, dans le groupe d’âge de 15 à 40 ans les femmes ont une mortalité plus élevée que les hommes, alors que dans le groupe 40 à 50 ans les hommes ont une mortalité plus élevée que les femmes.
La régularité interne de chacune des quatre séries d'estimations, la cohérence des estimations pour les deux périodes précédant l'enquête, et la plausibilité de la structure par âge de la mortalité évaluée par rapport aux standards externes, prouve que la méthode a bien fonctionné dans cette enquête du Bangladesh. Le trait le plus surprenant de ces résultats est la très forte baisse de la mortalité des adultes qui est suggérée dans la deuxième moitié des années 1990 au Bangladesh.
Fonctionnement dans les populations subissant une épidémie généralisée de VIH
L'épidémie de VIH pose deux problèmes pour les méthodes d'estimation de la mortalité basée sur la survie des apparentés (UN Population Division 1982). Premièrement, les deux modes de transmission (sexuelle et verticale) du virus créent un biais de sélection significatif dans les données recueillies sur la survie des parents. Deuxièmement, l'incidence de l'infection au VIH est concentrée chez les jeunes adultes. Ainsi, les populations qui font face à une mortalité importante causée par le sida ont des structures de mortalité par âge très différentes des autres populations et des systèmes de tables-types de mortalité existants.
Un avantage majeur que les méthodes basées sur la survie de la fratrie ont sur les méthodes de survie des parents pour mesurer la mortalité des adultes est qu'elles ne sont pas concernées par les biais de sélection découlant de la transmission directe du virus. Certains biais résiduels subsistent toutefois en raison de la concentration de la mortalité due au sida au sein des fratries. Tous les enfants nés d'une femme après qu'elle ait été infectée sont exposés au risque d'infection par transmission verticale. En outre, le risque d'infection par le VIH a tendance à varier considérablement entre les localités or, les frères et sœurs vivent souvent à proximité les uns des autres. L'effet de la proximité sera cependant relativement faible par rapport aux biais qui affectent les données que les parents ont fournies à propos de leurs enfants ou vice versa. En outre, les estimations directes de la mortalité basée sur la survie des frères et sœurs ont un avantage sur la méthode indirecte d’estimation également basée sur les fratries dans les populations à forte mortalité liée au sida en ce qu'elles mesurent la structure par âge de la mortalité directement – aucune hypothèse ne doit être faite à ce propos.
Extensions et variantes de la méthode
Afin d'extraire le maximum d'information utile des données sur les fratries en présence d’erreurs de déclaration et d'échantillonnage, les analystes ont eu recours à des modèles de régression appliqués aux données individuelles (au niveau des frères et sœurs) issues de plusieurs enquêtes et plusieurs pays pour contraindre quelque peu les résultats (par exemple, Obermeyer, Rajaratnam, Park et al 2010 ; Timæus and Jasseh 2004). Par exemple, Timæus et Jasseh intègrent un schéma par âge standard de mortalité à 2 paramètres dans leur modèle de régression du logarithmique des taux de mortalité afin de lisser les données. Ils font varier le coefficient de régression du standard (qui détermine la structure par âge de la mortalité) entre les pays, mais sans le faire changer au fil du temps. En outre, ils supposent que la vitesse de baisse de la mortalité pour des causes autres que le sida varie selon les pays mais qu’elle suit une tendance log-linéaire dans tous les pays. D'autres analystes ont des contraintes différentes sur leurs estimations.
Autres lectures et références
La méthode directe de calcul de la mortalité adulte à partir des histoires de fratries n’est pas abordée dans les manuels classiques sur l'estimation indirecte. Bien que leur rapport soit principalement axé sur la mesure de la mortalité maternelle, Stanton, Abderrahim et Hill (1997) discutent en détail d'un certain nombre de questions importantes relatives à l'estimation de la mortalité toutes causes confondues à partir des histoires de fratries, y compris l'imputation des dates exactes de naissance et de décès et le calcul des durées d'exposition. Les biais liés à la mortalité différentielle selon la taille des fratries et les problèmes associés au fait que certaines fratries sont mentionnées plusieurs fois sont discutés par Gakidou et King (2006), Masquelier (2013), et d'autres.
Blacker JGC and W Brass. 1983. "Experience of retrospective enquiries to determine vital rates," in Moss, L and H Goldstein (eds). The Recall Method in Social Surveys. London: University of London Institute of Education, pp. 48-61.
Coale AJ, P Demeny and B Vaughan. 1983. Regional Model Life Tables and Stable Populations. London: Academic Press.
Division de la Population des NU. 1984. Manuel X. Techniques indirectes d’estimation démographique. New York : Nations Unies, Département des affaires économiques et sociales internationales, ST/ESA/SER.A/81. https://unstats.un.org/unsd/demographic/standmeth/handbooks/Manuel_X-fr.pdf
Gakidou E and G King. 2006. "Death by survey: estimating adult mortality without selection bias from sibling survival data", Demography 43(3):569-585. doi: https://dx.doi.org/10.1353/dem.2006.0024
Graham W, W Brass and RW Snow. 1989. "Estimating maternal mortality: The sisterhood method", Studies in Family Planning 20(3):125-135. doi: https://dx.doi.org/10.2307/1966567
Hill K and TJ Trussell. 1977. "Further developments in indirect mortality estimation", Population Studies 31(2):313-334. doi: https://dx.doi.org/10.2307/2173920
Masquelier B. 2013. "Adult mortality from sibling survival data: A reappraisal of selection biases?", Demography, 50(1):207-228. doi: https://dx.doi.org/10.1007/s13524-012-0149-1
Obermeyer Z, JK Rajaratnam, CH Park, E Gakidou et al. 2010. "Measuring adult mortality using sibling survival: a new analytical method and new results for 44 countries, 1974-2006", PLoS Medicine 7(4):e1000260. doi: https://dx.doi.org/10.1371/journal.pmed.1000260
Rutenberg N and JM Sullivan. 1991. "Direct and indirect estimates of maternal mortality from the sisterhood method," Paper presented at Demographic and Health Surveys World Conference, August 5-7, 1991, Washington, D.C. Columbia. Macro International. Vol. 3:1669-1696.
Stanton C, N Abderrahim and K Hill. 1997. DHS Maternal Mortality Indicators: An Assessment of Data Quality and Implications for Data Use. Calverton: Macro International.
Timæus IM and M Jasseh. 2004. "Adult mortality in Sub-Saharan Africa: evidence from Demographic and Health Surveys", Demography 41(4):757-772. doi: https://dx.doi.org/10.1353/dem.2004.0037
Trussell J and G Rodriguez. 1990. "A note on the sisterhood estimator of maternal mortality", Studies in Family Planning 21(6):344-346. doi: https://dx.doi.org/10.2307/1966923
Zaba B. 1986. Measurement of Emigration using Indirect Techniques: Manual for the Collection and Analysis of Data on Residence of Relatives. Liège: Ordina.
Zaba B and PH David. 1996. "Fertility and the distribution of child mortality risk among women", Population Studies 50(2):263-278. doi: https://dx.doi.org/10.1080/0032472031000149346
- Printer-friendly version
- Log in to post comments
