Introduction aux tables-types de mortalité
Utilisation de tables-types pour l'estimation de la mortalité
On utilise des tables-types de mortalité comme références quand on examine des estimations empiriques de mortalité, pour lisser ou rectifier des valeurs défectueuses et pour compléter une table de mortalité quand on ne dispose d’estimations que pour certains groupes d’âge.
Dans ce contexte, le terme « lisser » renvoie à tout processus d’élimination ou de minimisation des irrégularités observées dans les données recueillies ou dans les premiers indices calculés à partir de ces données. Les techniques de lissage comprennent une grande variété de procédés, qui vont de l’ajustement de modèles au simple calcul de moyennes. Les techniques traditionnelles de lissage ou d’interpolation des structures par âge et des taux de mortalité par âge observés, comme le recours aux splines cubiques, sont décrites dans la littérature actuarielle et démographique, nous ne les aborderons pas ici. Nous nous intéresserons plutôt aux procédures fondées sur des modèles, indiquées quand les données de base sont défectueuses ou incomplètes.
En analyse démographique classique, on calcule une table de mortalité en transformant une série complète de taux de mortalité par âge (nmx) en quotients de mortalité (nqx). On peut alors en déduire les effectifs de survivants (l(x)) et les autres fonctions de la table. Mais, quand on analyse des données de recensement ou d’enquête, on n’obtient souvent des estimations de mortalité que pour une partie seulement des groupes d’âge. Par exemple, les estimations de mortalité calculées à partir des données d’une histoire génésique (Chapitre 17) ou d’une histoire des frères et sœurs (Chapitre 27) ne donnent aucune information sur la mortalité des jeunes sortis de la petite enfance ou sur celle des adultes de plus de 50 ans. Avec des estimations de ce genre, les tables-types de mortalité peuvent être utiles pour lisser les séries de taux de mortalité estimés et pour compléter la table de mortalité en formulant des hypothèses plausibles sur la valeur des taux aux âges auxquels la mortalité n’a pas pu être mesurée directement.
En outre, si on a évalué indirectement les probabilités de survie à partir d’informations sur les enfants nés vivants et survivants (Chapitre 16) ou sur la survie des parents (Chapitre 22) ou d’autres membres adultes de la famille, les résultats ne donnent que le niveau de la mortalité dans les grandes catégories d’âge. En particulier, pour les adultes, ces méthodes fournissent des probabilités conditionnelles de survie, c’est-à-dire des probabilités de survie de l’âge A à l’âge B, l(B)/l(A). Dans ce cas, on peut utiliser des tables-types à la fois pour estimer les taux de mortalité par groupes quinquennaux d’âge et pour compléter la table en faisant une hypothèse acceptable sur la mortalité aux grands âges.
Les deux chapitres qui suivent présentent deux manières de construire des tables de mortalité complètes à partir de données sur la mortalité dans certains groupes d’âge seulement. Le Chapitre 32 porte sur les méthodes qui combinent une estimation isolée de la mortalité infanto-juvénile (5q0) et une estimation de survie conditionnelle adulte de la même année ou de la même période, pour en déduire une table de mortalité complète. Plusieurs variantes de cette méthode sont présentées. Le Chapitre 33 décrit une méthode qui combine une série d’estimations datées de mortalité infanto-juvénile (comme celles que l’on déduit indirectement des informations sur les enfants nés vivants et les enfants survivants) et une série d’estimations datées de probabilités conditionnelles de survie à l’âge adulte (comme celles fournies par les méthodes indirectes d’exploitation des informations sur la survie des parents ou des frères et sœurs), pour obtenir la table de mortalité relative à une date déterminée.
Dans ce manuel, nous utilisons abondamment les tables-types de mortalité fondées sur des modèles relationnels logit, premièrement pour évaluer et lisser des séries d’estimations de mortalité des enfants et de mortalité adulte, et deuxièmement pour combiner des estimations indépendantes de mortalité des enfants et de mortalité adulte afin d’obtenir des tables complètes. Le système et ses propriétés font l’objet de la section suivante.
Vue d’ensemble du système relationnel logit de tables-types de mortalité
Brass et ses collègues (Brass, 1964, 1971 ; Brass et Coale, 1968) ont développé un système flexible à deux paramètres de tables-types de mortalité couramment appelé système relationnel logit de tables-types de mortalité. En gros, le premier paramètre, α, représente les écarts de niveau de mortalité entre populations différentes, et le deuxième, β, représente la variabilité d’une population à l’autre du rapport entre mortalité des enfants et celle des adultes.
Ce système de modèles est de type relationnel. C’est-à-dire qu’il est basé sur une transformation mathématique de la fonction de survie par âge, l(x), qui permet de relier entre elles, par une simple équation, deux tables de mortalité différentes. En particulier, Brass a découvert qu’une transformation logit des probabilités de survie jusqu’à l’âge x, l(x), rendait à peu près linéaire la relation entre les probabilités transformées de différentes tables de mortalité.
Donc, si on définit le logit de l(x) comme :
(1)
la relation linéaire suivante se vérifie approximativement à tous les âges :
(2)
Y(x) et Y*(x) étant les logits des probabilités de survie par âge, l(x) et l*(x), de deux tables de mortalité différentes, et α et β étant des paramètres constants.
Les habitués de la régression logistique reconnaîtront dans Y(x) la moitié du logarithme du rapport de cotes (odds) de la probabilité de décès entre la naissance et l’âge x, puisque :
Si l’équation 2 était vérifiée pour toute paire de tables de mortalité, cela signifierait qu’il serait possible de calculer n’importe quelle table de mortalité à partir d’un même modèle de référence, appelé le standard de mortalité, ls(x), en donnant des valeurs appropriées aux paramètres α et β. En réalité, l’équation n’est qu’approximativement satisfaite par des paires de tables de mortalité réelles, mais l’approximation est assez bonne pour permettre le recours à cette relation pour étudier et modéliser des schémas de mortalité observés.
Avant d’expliquer comment utiliser l’équation 2 pour calculer des tables-types de mortalité, arrêtons-nous un instant sur la signification des paramètres α et β. Considérons l’ensemble des tables de mortalité qui peuvent être calculées à partir d’une certaine table-type, ls(x), et de différentes valeurs de α et β. Si β est maintenu constant et égal à 1, modifier la valeur de α va soit augmenter soit diminuer les probabilités de survie à chaque âge. Donc, modifier α va engendrer des tables de mortalité dont le profil est essentiellement celui de la table-type ls(x) utilisée pour les construire, mais dont le niveau général de mortalité varie. Si, en revanche, on donne à α la valeur 0 et si on laisse β varier, les tables obtenues n’auront plus le même profil que ls(x). Toutes les tables ainsi calculées auront une intersection commune en un point unique, situé quelque part vers le milieu de l’éventail des âges, où ls(x) = 0,5 et Ys(x) = 0. Leurs probabilités de survie seront alors soit plus faibles aux âges jeunes et plus fortes aux âges élevés, soit plus fortes aux âges jeunes et plus faibles aux âges élevés, que celles de la table-type qui a servi à les calculer. Ainsi, β affecte la structure de la mortalité calculée plutôt que son niveau. Des variations simultanées de α et β feront varier à la fois le niveau et la structure de la fonction de survie calculée.
On peut déduire de l’équation 1 l’équivalence suivante :
et en combinant ceci avec l’équation 2, on obtient :
(3)
Ainsi, à partir d’une série quelconque de valeurs de ls(x) définissant une table-type de mortalité, on peut obtenir une autre série l(x) associée à chaque couple formé d’une valeur de α et d’une valeur de β. (Notons que, aux extrémités de l’éventail des âges, on ne peut plus utiliser l’équation 3 pour calculer l(x) : on doit affecter les valeurs 1 et 0 à l(0) et l(ω) respectivement.)
L’équation 3 peut servir au calcul de familles de tables-types de mortalité à partir d’une table choisie comme standard, ls(x). En principe, n’importe quelle table de mortalité peut être retenue comme standard. Par exemple, on peut choisir une table de mortalité fiable, mais relative à une autre date, de la population concernée ou une table de mortalité d’un pays voisin. Mais, quand on n’a pas de telles tables fiables ou appropriées sous la main, on prend souvent comme standard une table-type extraite des tables-types régionales de Princeton (Coale, Demeny et Vaughan, 1983) ou des tables-types de mortalité des Nations Unies pour les pays en développement (UN Population Division, UN Model Life Tables for Developing Countries, 1982). Le choix des tables standards employées dans ce manuel est expliqué dans la section suivante.
Du fait de la simplicité mathématique des équations 2 et 3, les tables-types obtenues à l’aide d’un modèle relationnel logit et basées sur un standard quelconque, se calculent facilement dans un tableur, ce qui évite de devoir manipuler de grandes quantités de tables publiées. La forme mathématique simple de l’équation 3 facilite également l’emploi du modèle relationnel logit des tables-types pour procéder à des simulations ou des projections de mortalité. Si on connaît les structures passées et actuelle de la mortalité d’une population, on peut déterminer les tendances des paramètres α et β en appliquant le modèle relationnel logit de tables-types à chacune d’elles, et on peut, moyennant quelques précautions, projeter ces deux paramètres pour obtenir des estimations de la mortalité future.
Description des tables-types de mortalité utilisées dans ce manuel
Toutes les tables de mortalité exprimées sous forme logit dans ce manuel sont basées sur une même série de tables standards. Celles-ci sont empruntées aux tables-types régionales de Princeton (Nord, Sud, Est et Ouest) et aux tables-types des Nations Unies pour les pays en développement (modèle général, Amérique Latine, Chili, Asie du Sud, Extrême-Orient), sexes séparés. Toutes ont une espérance de vie à la naissance de 60 ans. Les tables originales ont été modifiées, étendues et améliorées au fil du temps pour pouvoir être appliquées aux âges élevés. Nous utilisons les tables actualisées que la Division de la population des Nations Unies a développées et employées dans ses projections démographiques (UN Population Division 2013). Elles fournissent les valeurs de l(x) et de Lx (entre autres) pour les âges 0, 1, 5, 10, …, 130 ans.
Pour les tables standards basées sur les tables-types régionales de Princeton, les valeurs de l(2), l(3) et l(4) ont été déterminées en appliquant les multiplicateurs proposés par Coale, Demeny et Vaughan (1983, p. 21) à l(1) et l(5). Pour les tables standards basées sur les tables-types des Nations Unies pour les pays en développement, les décès entre 1 et 5 ans ont été répartis par année d’âge dans les mêmes proportions que dans les tables de mortalité par sexe et par région originales (UN Population Division 1982).
Certaines méthodes d’estimation de la mortalité des enfants et des adultes nécessitent des tables de mortalité sexes confondus (c’est-à-dire sans distinction de sexe). Comme ces tables (ou leur mise en œuvre) ne sont pas particulièrement sensibles au rapport de masculinité à la naissance, on a fixé celui-ci à 105 garçons pour 100 filles. Les tables de mortalité sexes confondus ont alors été calculées en appliquant les pondérations appropriées aux tables pour les deux sexes séparés :
où lc(x) représente le nombre de survivants à l’âge x de la table sexes confondus, et lm(x) et lf(x) étant les valeurs correspondantes pour le sexe masculin et le sexe féminin.
Comme ces tables de mortalité sont utilisées presque exclusivement dans un contexte relationnel (comme Brass (1971) l’a prévu initialement), les logits standards des ls(x) ont été calculés pour tous les âges supérieurs à zéro au moyen de la formule suivante :
Les valeurs numériques de ces logits peuvent être téléchargées sur le site web Tools for Demographic Estimation.
Le choix du standard
Il y a un choix capital à faire lors de la mise en œuvre de méthodes basées sur les tables-types de mortalité ou quand on combine des estimations obtenues par différentes méthodes pour construire une table unique à l’aide du système relationnel de tables-types, c’est le choix de la table standard qui servira de base aux calculs.
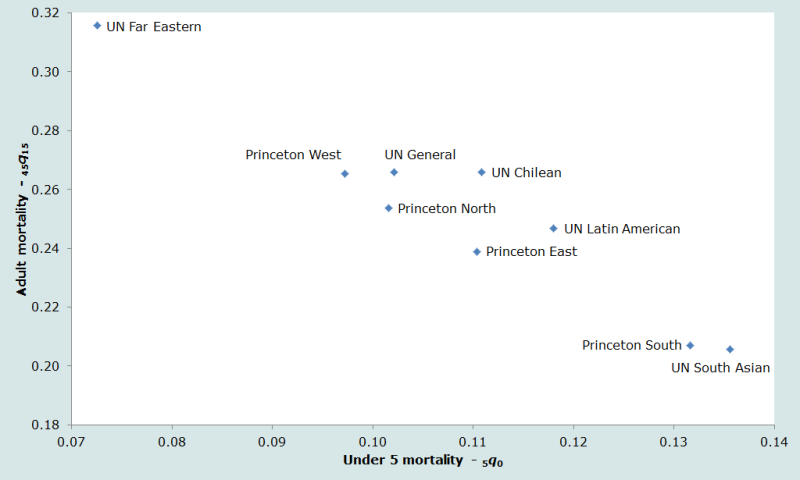
Les neuf tables de mortalité standards (quatre tables-types régionales de Princeton et cinq tables-types des Nations Unies pour les pays en développement) employées dans ce manuel représentent des schémas de mortalité très différents. La figure 1 montre la relation entre la mortalité des enfants et la mortalité adulte des tables standards sexes confondus – qui ont toutes une espérance de vie à la naissance de 60 ans. L’indice de mortalité des enfants est 5q0, la probabilité de mourir entre la naissance et le 5e anniversaire ; l’indice de mortalité adulte est 45q15, la probabilité de décéder entre 15 et 60 ans (conditionnelle au fait d’avoir survécu à 15 ans).
Ainsi, par exemple, la table Extrême-Orient des Nations unies s’avère avoir une mortalité adulte très élevée et une mortalité des enfants très faible, comparativement aux autres tables utilisées, alors que, à l’autre extrême, les tables Sud de Princeton et Asie du Sud des Nations unies ont une mortalité adulte relativement faible, mais une mortalité des enfants très élevée.
Un autre point de divergence entre ces diverses tables est le rapport entre la mortalité infantile (avant le 1er anniversaire) et la mortalité juvénile (entre les 1er et 5e anniversaires). En comparant ces quotients (figure 2), on voit que, si les tables Extrême-Orient et Chili des Nations Unies ont à peu près le même niveau de mortalité juvénile, leurs niveaux de mortalité infantile sont très différents.
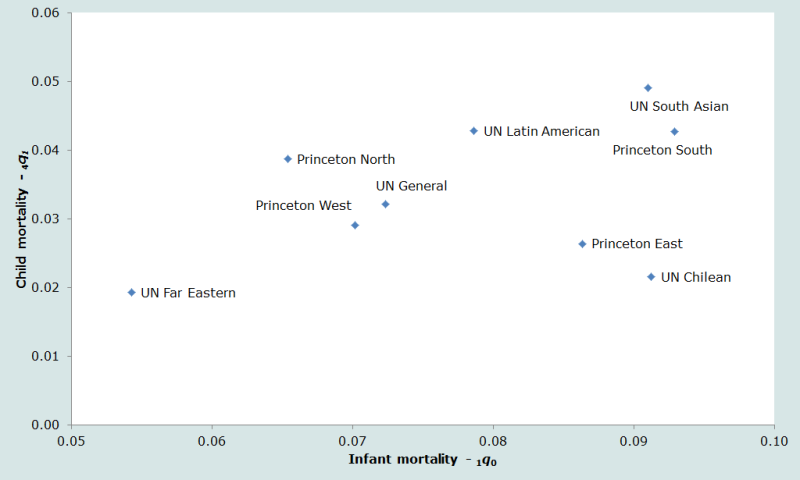
Idéalement, le choix d’une table standard devrait refléter au mieux le rapport entre mortalité infantile et mortalité juvénile, d’une part, et le rapport entre mortalité des enfants et mortalité adulte, d’autre part. Ainsi, si on dispose d’une estimation acceptable du schéma de mortalité d’un pays donné, on déterminera la meilleure table standard en comparant le schéma de mortalité observé avec ceux des tables-types. Mais quand l’analyste n’a pas, ou presque pas, d’informations fiables sur la mortalité par âge, il ne peut faire mieux que choisir le schéma qui lui paraît le plus approprié.
Dans les situations où on ne sait rien du schéma de mortalité par âge, il est recommandé d’utiliser soit le modèle Ouest de Princeton, soit le modèle général des Nations Unies, parce que ces tables-types ont été construites à partir d’un éventail de données relativement large. En outre, le modèle général des Nations unies, en particulier, peut être considéré comme un schéma moyen par rapport aux paramètres des figures 1 et 2.
Quant aux « renseignements complémentaires » qui pourraient aider à faire un choix pertinent, ils varient considérablement en genre et en qualité. Ils peuvent aller, par exemple, de taux de mortalité par âge estimés à partir de données d’état civil à la connaissance de quelques traits généraux comme la prévalence et la durée habituelle de l’allaitement maternel dans la population étudiée ou une estimation de la prévalence de la tuberculose.
Quand on dispose d’une série de taux de mortalité par âge observés (de préférence ajustés au moyen d’une méthode de répartition des décès comme celles qui sont décrites aux Chapitres 24 et 25), on peut choisir un schéma standard de mortalité en comparant les logits des l(x) observés à ceux des diverses tables-types de mortalité. Cette comparaison peut être menée à bien en portant sur un graphique la relation entre les valeurs observées de Y(x) et celles qui résultent des diverses tables-types, et en retenant la table-type qui présente la relation la plus linéaire entre les deux séries de valeurs.
À considérer la description donnée plus haut des schémas de mortalité des diverses tables-types, on voit d’emblée qu’ils diffèrent très nettement en termes de valeurs aux premiers âges et de rapport entre mortalité infantile (1q0) et mortalité juvénile (4q1). Il s’ensuit que des estimations très différentes de la mortalité des enfants peuvent être déduites des mêmes données observées selon la famille de tables-types que l’on aura retenue. De plus, en pareil cas, il peut être difficile de trouver des renseignements extérieurs solides qui aident au choix d’un standard, principalement parce que, bien souvent, les décès infantiles sont largement sous-déclarés. En l’absence de données empiriques sérieuses qui orientent le choix d’une table de mortalité standard adéquate, on peut suggérer quelques lignes de conduite générales qui réduisent l’éventail des possibilités et mènent à un choix raisonnable :
a) Dans une population où l’allaitement maternel est couramment pratiqué et où le sevrage est relativement tardif (au-delà de 12 mois), on peut raisonnablement s’attendre à une mortalité juvénile (4q1) relativement élevée comparativement à la mortalité infantile (1q0), étant donné que l’allaitement maternel peut s’avérer efficace pour prévenir des décès dus à la malnutrition et aux maladies infectieuses chez les nourrissons. Mais, au moment du sevrage, l’enfant est moins protégé contre ces dangers et donc plus exposé à un risque de décès plus élevé. Dans ce cas, la mortalité des enfants sera probablement bien représentée par le modèle Nord de Princeton ou le modèle général des Nations Unies. Toutefois, on ne peut pas déduire de cette observation que ces tables-types représenteront correctement la mortalité aux autres âges. Seules des informations indépendantes sur la mortalité adulte peuvent étayer cette conclusion.
b) Dans certaines populations d’aujourd’hui, l’allaitement maternel a été abandonné par une grande partie de la population féminine, et, dès leur plus jeune âge, les bébés reçoivent des doses de « lait maternisé » non stériles et souvent inadéquates. Quand cette pratique est adoptée par des mères qui vivent dans un environnement relativement insalubre et que s’y ajoutent de mauvaises conditions d’assistance lors de l’accouchement et dans les heures qui suivent (ce qui peut conduire à une fréquence élevée de tétanos néonatal), la mortalité infantile peut être élevée comparativement à la mortalité des enfants plus âgés. Dans un tel contexte, le modèle Est de Princeton ou le modèle chilien des Nations unies peuvent représenter correctement la mortalité des enfants. L’avertissement du paragraphe précédent reste valable : il convient de s’assurer que ces tables rendent bien compte du rapport entre mortalité des enfants et mortalité adulte.
c) Le sevrage précoce n’est pas la seule cause de malnutrition susceptible d’entraîner une mortalité infanto-juvénile élevée. Chez certaines populations, l’allaitement maternel est quasi universel, mais, l’hygiène et l’état nutritionnel des enfants étant insuffisants, la mortalité infantile et la mortalité juvénile sont élevées. Pour les pays peu développés de ce genre, le modèle Sud de Princeton ou le modèle sud-asiatique des Nations Unies peuvent être les plus adaptés.
d) En l’absence de données permettant de sélectionner la famille de tables-types qui convient le mieux à un pays donné, on peut choisir la famille qui a été utilisée dans le cas d’un pays voisin dont les caractéristiques culturelles et socio-économiques sont similaires.
e) Pour les raisons exposées plus haut, si on ne connaît pas grand-chose sur la population concernée, on recommande d’utiliser le modèle Ouest de Princeton ou le modèle général des Nations Unies.
Suite à ces remarques, il est clair que nos connaissances sur les schémas de mortalité sont encore assez limitées et que, de toute évidence, de meilleurs renseignements sur la mortalité des populations des pays en développement sont nécessaires pour évaluer la pertinence des modèles disponibles.
Autres systèmes de tables-types de mortalité
Deux des méthodes d’ajustement des tables de mortalité aux données observées qui seront présentées dans le chapitre suivant reposent sur deux autres approches de la modélisation des schémas de mortalité, qui diffèrent quelque peu du travail pionnier de Brass. Nous allons décrire brièvement ces deux autres systèmes de tables-types de mortalité. Pour des renseignements plus complets, nous renvoyons le lecteur intéressé à la littérature correspondante.
Le système logit modifié
Murray et ses collègues (Murray, Ferguson, Lopez et al., 2003) ont proposé un système relationnel logit modifié basé sur une table standard générale unique et deux séries de paramètres par âge supplémentaires, γ(x) et θ(x) :
Comme précédemment, Y(x) représente la transformation logit de l(x). Les deux premiers paramètres sont ceux du système relationnel logit de Brass. Le premier des deux paramètres additionnels, γ(x), relie la probabilité de survie des enfants de moins de 5 ans au standard, tandis que θ(x) joue le même rôle pour le niveau de survie des adultes.
Bien qu’à première vue on ait affaire à quatre paramètres, cette version modifiée du système relationnel logit reste en fait un modèle à deux paramètres. Puisqu’on donne par définition la valeur zéro à γ(5), θ(5), γ(60) et θ(60), α et β suffisent à déterminer l(5) et l(60) dans le modèle ajusté, et donc aussi les deux séries d’écarts par âge par rapport au schéma standard de mortalité, γ(x) et θ(x). En réalité, ces écarts servent à réduire l’impact qu’a sur la mortalité dans l’enfance et aux grands âges l’utilisation d’une valeur de β autre que 1 pour modéliser la relation globale entre mortalité des enfants et mortalité adulte.
Les utilisateurs de ce système de modèles doivent être avertis que les valeurs de γ(x) et θ(x) publiées dans l’article de 2003 sont affectées d’un signe erroné. Les paramètres du tableau 3 de cet article doivent donc être multipliés par –1 avant toute utilisation.
Le système log-quadratique
Un autre système de tables-types de mortalité à deux paramètres a été publié récemment par Wilmoth, Zureick, Canudas-Romo et al. (2012). Il met en relation quatre constantes scalaires par âge, a(x), b(x), c(x) et v(x), et deux paramètres, h et k, de la manière suivante :
Les valeurs de a(x), b(x), c(x) et v(x) ont été calculées à partir des données de mortalité de la Human Mortality Database ; avec les deux paramètres restants (h et k), on ajuste le modèle aux estimations empiriques de la mortalité.
Le premier paramètre, h, mesure le niveau général de la mortalité ; il est défini comme le logarithme du 5q0 observé. Le second, k (combiné avec v(x)), représente l’écart entre la structure par âge de la mortalité observée et celle d’une population standard. En pratique, il est choisi pour s’ajuster à un indice observé, ou une série d’indices observés, de la mortalité adulte (par exemple 45q15 ou 30q30).
Références
Brass W. 1964. Uses of census or survey data for the estimation of vital rates. Paper prepared for the African Seminar on Vital Statistics, Addis Ababa 14-19 December 1964. Document No. E/CN.14/CAS.4/V57. New York: United Nations.
Brass W. 1971. "On the scale of mortality," in Brass, W (ed). Biological Aspects of Demography. London: Taylor and Francis, pp. 69-110.
Brass W and AJ Coale. 1968. "Methods of analysis and estimation," in Brass, W, AJ Coale, P Demeny, DF Heisel, et al. (eds). The Demography of Tropical Africa. Princeton NJ: Princeton University Press, pp. 88-139.
Coale AJ, P Demeny and B Vaughan. 1983. Regional Model Life Tables and Stable Populations. New York: Academic Press.
Murray CJ, BD Ferguson, AD Lopez, M Guillot, J Salomon and O Ahmad. 2003. "Modified logit life table system: principles, empirical validation, and application", Population Studies 57(2):165-182. doi: 10.1080/0032472032000097083
UN Population Division. 1982. Model Life Tables for Developing Countries. New York: United Nations, Department of Economic and Social Affairs, ST/ESA/SER.A/77. https://www.un.org/development/desa/pd/sites/www.un.org.development.desa.pd/files/files/documents/2020/Jan/un_1982_model_life_tables_for_developing_countries.pdf
UN Population Division. 2011. Model Life Tables. New York: United Nations, Department of Economic and Social Affairs. https://www.un.org/development/desa/pd/data/model-life-tables
UN Population Division. 2013. World Population Prospects: The 2012 Revision. New York: United Nations, Department of Economic and Social Affairs. https://www.un.org/development/desa/pd/sites/www.un.org.development.desa.pd/files/files/documents/2020/Jan/un_2012_world_population_prospects-2012_revision_highlights.pdf
Wilmoth JR, S Zureick, V Canudas-Romo, M Inoue and C Sawyer. 2012. "A flexible two-dimensional mortality model for use in indirect estimation", Population Studies 66(1):1-28. doi: https://dx.doi.org/10.1080/00324728.2011.611411
- Printer-friendly version
- Log in to post comments
