Méthode de l’extinction des cohortes synthétiques
Description de la méthode
Les démographes Neil Bennett et Shiro Horiuchi (Bennett et Horiuchi 1981, 1984) ont proposé une généralisation de la méthode de Preston et Coale pour estimer la complétude de la déclaration des décès par rapport à une estimation de la population, et qui est maintenant connue sous le nom de la méthode de l’extinction des cohortes synthétiques (Synthetic Extinct Generations (SEG) method). Ces deux méthodes partent du même constat que, dans une population fermée, le nombre de personnes d’âge a survivantes à un instant t doit être égal au nombre de décès cumulés au-delà du temps t dans la même cohorte. Le principe de base sur lequel se fondent les méthodes de l’extinction des cohortes synthétiques est que le flux de décès à venir dans une cohorte peut être estimé par les décès d’âge a se produisant au temps t corrigés en tenant compte de la croissance démographique. Le cas le plus simple, mais très particulier, est celui d’une population stationnaire, associée à une table de mortalité, dans laquelle le nombre de décès d’âge a au temps t sera égal aux décès d’âge a dans la même cohorte. Un cas plus général, mais un peu plus complexe, est celui d’une population stable, c'est-à-dire une population fermée aux migrations, croissant à un taux constant r, et ayant une mortalité par âge constante et une structure par âge constante. Dans ce cas, si les données déclarées sont complètes et précises, le nombre de décès à l’âge x dans t années sera égal au nombre de décès mesuré à un instant précis multiplié par le coefficient de la croissance démographique, soit . C’est cette relation qui fonde la méthode de Méthode de Preston et Coale.
Dans le cas encore plus général dans lequel la population n’est pas stable, on peut trouver une relation équivalente en remplaçant : par , où r(y,t) représente le taux de croissance instantané de la population d’âge y au temps t.
Si les décès déclarés au temps t sont sous-déclarés dans la même proportion, c, à tous les âges, au moins pour les âges adultes, alors le nombre de décès attendus dans la cohorte sera sous-estimé dans la même proportion. On pourra donc estimer la complétude de la déclaration des décès en divisant la somme des estimations du nombre de décès attendus dans le futur dans la cohorte calculées d’après les décès mesurés à l’instant t par la population mesurée à la même date. On pourra ainsi recalculer les taux de mortalité du moment en divisant le nombre de décès déclarés dans chaque groupe d’âge par le coefficient c, puis en divisant ces nombres corrigés par une estimation de la population au risque, ce qui permettra de recalculer les taux partiels de natalité et de mortalité.
Données requises et hypotheses
Tabulation des données requises
- Les effectifs de femmes (ou d’hommes), répartis par groupe d’âge de cinq ans, et pour l’intervalle d’âge ouvert A+ (avec A aussi élevé que possible), à deux instants donnés, le plus souvent provenant de deux recensements (voir ci-dessous les inconvénients qui résultent de l’utilisation d’enquêtes par sondage au lieu de recensements).
- Les nombres de décès de femmes (ou d’hommes), répartis par groupe d’âge de cinq ans, et pour l’intervalle d’âge ouvert A+, pour toute la période située entre les deux recensements ou les deux enquêtes.
Hypothèses importantes
- La couverture de chaque recensement est la même à tous les âges
- La complétude de la déclaration des décès est la même à tous les âges au-delà d’un âge minimal (en général 15 ans)
- La population est fermée aux migrations. La méthode pourra être adaptée aux cas des migrations, mais on ne dispose que très rarement des effectifs de migrations nettes par âge. Pour les populations nationales, les migrations nettes sont souvent suffisamment faibles pour être négligées, mais lorsque ce n’est pas le cas, il conviendra de prendre en compte les migrations lorsqu’on interprétera les résultats et que l’on devra retenir une estimation finale de la complétude.
Travaux préparatoires et recherches préliminaires
Avant de mettre en œuvre cette méthode, on doit au préalable analyser la qualité des données, et au moins les points suivants:
- structure par âge de la population;
- structure par sexe de la population;
- structure par âge des décès; et
- structure par sexe des décès.
Si la période au cours de laquelle les décès sont déclarés est différente de celle située entreles deux recensements, il faudra corriger ces nombres pour estimer ceux qui se sont produits dans la période intercensitaire. Lorsqu’on dispose de données de l’état civil, cet ajustement consistera à répartir proportionnellement les décès des années correspondant aux années des deux recensements, c'est-à-dire la première et la dernière année de la période. Lorsqu’on dispose des décès déclarés par les ménages au cours des 12 mois précédents chacun des recensements, on doit estimer le nombre de décès de la période intercensitaire par interpolation (voir la feuille de calcul suivante : AM_Estimating deaths).
La méthode de l’extinction des cohortes synthétiques utilise des taux de croissance par âge pour effectuer ces calculs. Si la couverture du décompte de population varie d’un recensement à l’autre, dans un rapport constant par âge, alors les taux de croissance par âge vont être systématiquement biaisés, d’une quantité fixe, notée delta. La méthode généralisée de la balance de l’accroissement démographique permet d’ailleurs de calculer directement ce biais. Par contre la méthode de l’extinction des cohortes synthétiques ne permet pas d’estimer directement delta, mais des valeurs non-nulles de delta se traduisent par une tendance linéaire dans les estimations de la complétude par âge. On pourra alors estimer delta par itération, en recherchant la valeur qui produit des estimations de la complétude constantes par âge sur un intervalle situé entre deux âges, minimal et maximal.
Précautions et mises en garde
Lorsqu’ils appliquent cette méthode, les analystes doivent prendre en considération les points suivants :
- Le processus d’interprétation et d’estimation doit prendre en compte la source des données de mortalité (décès déclarés à l’état civil, décès déclarés par les ménages dans les recensements, ou décès déclarés dans les structures sanitaires), comme cela est expliqué plus loin. Les biais associés à la source des données tendent à avoir plus d’effet sur l’estimation de la complétude avec la méthode de l’extinction des cohortes synthétiques qu’avec la méthode généralisée de la balance de l’accroissement démographique.
- Le problème des migrations devient plus sérieux quand on applique la méthode à des zones géographiques régionales, et non plus nationales.
- Il est nécessaire de choisir correctement l’intervalle d’âges pour calculer delta (l’estimation relative de la couverture d’un recensement par rapport à l’autre). Les problèmes spécifiques sont les suivants : est-ce que la meilleure estimation de delta est fournie par l’ordonnée à l’origine obtenue par application de la méthode généralisée de la balance de l’accroissement démographique aux mêmes données (ce qui peut être le cas, par exemple, si on pense que le sous-enregistrement des décès augmente après l’âge à la retraite, pour des raisons expliquées ci-dessous) ? Est-ce qu’il convient d’exclure les âges en dessous de 30 ou 35 ans, car l’impact des migrations n’y est pas pris en compte spécifiquement ?
- Il est nécessaire de choisir correctement l’intervalle d’âges pour calculer la complétude. En général, cet intervalle d’âge pourrait exclure les jeunes adultes lorsqu’on suspecte de fortes migrations qui ne sont pas prises en compte, ou exclure les personnes âgées si les résultats indiquent que leurs décès sont moins bien déclarés que ceux des jeunes adultes, ou si les erreurs sur l’âge des personnes âgées semble affecter différemment les âges des survivants et ceux des décédés.
- Il convient de s’assurer que le module Solveur de Excel a fonctionné correctement, c’est à dire qu’il a fourni des résultats réalistes. Il peut arriver que le module Solveur fournisse une solution qui soit manifestement trop basse. Dans de telles situations, il est préférable d’ajuster delta à la main dans la bonne direction, et de faire tourner le module Solveur en démarrant par cette nouvelle valeur.
- Il convient de s’assurer que l’estimation de l’espérance de vie dans le groupe d’âge ouvert est réaliste. Il arrive souvent que les données sur les décès des personnes âgées sont rares et sujettes à des erreurs. Les estimations de l’espérance de vie qui en résultent peuvent être irréalistes, surestimant le plus souvent l’espérance de vie. Plus l’âge au début de l’intervalle ouvert est élevé, plus l’impact de ce type d’erreur sera faible.
- Lorsque la complétude des décès déclarés semble être inférieure à 60 %, on conseille de prendre garde aux résultats, car l’incertitude sur les estimations devient importante.
- Dans le cas où les données sur la population et les décès des ménages sont collectées lors d’un recensement unique, il est tentant de chercher à utiliser des données d’une enquête par sondage pour avoir une répartition par âge de la population à une autre date, antérieure ou postérieure, de manière à pouvoir utiliser la méthode. Mais, pour des raisons qui ne sont pas claires et qui n’ont pas fait l’objet de recherches approfondies, une telle combinaison de sources de données très différentes donne rarement des résultats satisfaisants.
Application de la méthode
D’un point de vue purement technique, on pourrait appliquer cette méthode à des données présentées par année d’âge, mais ce type de données est sujet à de fortes erreurs sur l’âge, si bien que, en pratique, on travaille le plus souvent avec des données présentées par groupe d’âge de 5 ans. Comme la plupart des données disponibles sont publiées selon ce format, la feuille de calcul correspondante est organisée pour travailler avec des groupes d’âge quinquennaux classiques. Il faut remarquer que John Blacker (Blacker 1988) a montré que ces groupes d’âge classiques sont sensibles aux préférences pour les chiffres ronds ; dans ce cas on pourra adapter la méthode pour travailler avec des groupes d’âge quinquennaux différents, centrés sur les chiffres qui font l’objet de l’attraction (12-17, 18-21 etc.), plutôt qu’avec des groupes d’âge commençant par ces chiffres (15-19, 20-24, etc.).
Etape 1: Lorsque ce nombre n’est pas immédiatement disponible, estimation du nombre de décès déclarés au cours de la période entre les deux recensements de population
Dans le cas où l’on dispose de données de l’état civil par année de calendrier, l’ajustement consiste à répartir proportionnellement les décès de la première et de la dernière année. On les répartit proportionnellement à la fraction de l’année couverte après le premier recensement et avant le second recensement. Sauf si la distribution des décès par âge change très rapidement au cours de l’année, cette approximation n’aura pas d’effet notable sur les résultats.
Dans le cas où l’on ne dispose pas des décès entre les deux enquêtes, mais si l’intervalle tombe entre deux périodes pour lesquelles on a de telles données (par exemple dans le cas où chaque recensement inclut la question sur les décès des douze derniers mois dans le ménage), on peut alors utiliser la feuille de calcul suivante : AM_Estimating deaths. Cette feuille de calcul permet d’estimer le nombre de décès entre deux instants donnés d’après les décès qui se sont produits au-cours de deux périodes les encadrant. Pour utiliser cette feuille de calcul, on a besoin du nombre de décès répartis par groupes d’âge quinquennaux pour les deux périodes, les dates de début et de fin de chaque période, ainsi que les dates de début et de fin de la période au cours de laquelle on veut estimer le nombre de décès.
Etape 2 : Calcul des taux de croissance par âge, après correction pour tenir compte des migrations et de la différence de couverture entre les deux recensements
Les taux de croissance par âge, après correction pour tenir compte des migrations et de la différence de couverture des deux recensements, se calculent à partir des deux recensements, et du nombre de migrants au cours de la période intercensitaire, répartis par groupe d’âge, comme suit :
où est la population du groupe d’âge x à x + 5 à l’instant t, 5NMx est le nombre de migrations nettes (immigrants moins émigrants) dans le groupe d’âge x à x + 5, et t1 et t2 sont les dates moyennes des deux recensements. Delta (δ) représente la correction à effectuer pour prendre en compte la différence de couverture des deux recensements. On le calcule soit en utilisant la méthode de la balance de l’accroissement démographique, soit par itération comme cela est expliqué plus loin.
Etape 3: Calcul de l’espérance de vie à l’âge A et au début de chaque groupe d’âge quinquennal, jusqu’à 65 ans
On peut faire ce calcul de plusieurs manières :
1) Utiliser une estimation provenant d’autres sources fiables, s’il en existe. Ce peut être une estimation provenant de recherches antérieures, ou une estimation tirée des projections de population comme celles fournies par les Perspectives de la population mondiale (UN Population Division 2011).
2) Utiliser une estimation calculée à partir des mêmes données auxquelles on a appliqué la méthode de la balance de l’accroissement démographique. Le classeur Excel qui correspond à cette méthode fournit, parmi ses résultats, une telle estimation.
3) Utiliser une table-type de mortalité. Pour cela, on pourra calculer le rapport des décès dans les groupes d’âge 10-39 ans et 40-59 ans (âge au dernier anniversaire), soit (30D10/20D40), comme entrée dans le système des tables-type. Ce rapport pourra être comparé à celui du modèle Ouest des tables-type de Princeton, qui servira à calculer l’espérance de vie. On trouvera dans le classeur Excel correspondant une feuille de calcul qui effectue ces calculs. Mais, comme le modèle Ouest des tables-type de Princeton ne permet pas d’ajuster un schéma par âge résultant des décès causés par le VIH/sida, cette approche ne convient pas aux pays qui souffrent d’une forte mortalité par sida.
4) Utiliser une méthode itérative: on part d’une valeur raisonnable, que l’on peut prendre dans une table-type du modèle Ouest de Princeton (sauf si le pays souffre d’une forte mortalité par sida), ou provenant d’une source indépendante. Ensuite, on estime la complétude, comme cela est expliqué plus loin, on recopie les nouvelles valeurs de l’espérance de vie après correction pour tenir compte du sous-enregistrement dans la feuille de calcul Espérances de vie du classeur Excel, on les colle dans la feuille de calcul Méthode du classeur Excel et on recommence l’estimation de la complétude. On peut répéter l’opération plusieurs fois si nécessaire, jusqu’à ce que l’estimation devienne stable, c'est-à-dire que les variations de l’espérance de vie deviennent négligeables. Malheureusement, s’il y a de bonnes raisons de penser que la mortalité reste sous-estimée aux âges élevés, même après correction du sous-enregistrement (par exemple si les âges sont exagérés, ou si le niveau de complétude baisse avec l’âge), alors cette approche va tendre à surestimer les espérances de vie, et par conséquent à surestimer le niveau de complétude de la déclaration des décès.
Etape 4 : Calcul du nombre de personnes qui atteignent l’âge x, et ceux qui atteignent le groupe d’âge x à x+4, d’après le nombre de décès déclarés
Le nombre de personnes qui atteignent l’âge x au cours de la période de référence, c'est-à-dire celle au cours de laquelle les décès sont déclarés, se calcule à partir des décès déclarés comme suit :
et
où A désigne le début de l’intervalle ouvert, nrx est le taux de croissance annuel dans le groupe d’âge de x à x+n (âge au dernier anniversaire), et eA est l’espérance de vie à l’âge A.
Le nombre de personnes qui atteignent le groupe d’âge de x à x+4 (âge au dernier anniversaire), pendant la période de référence, se calcule d’après les nombres de personnes qui atteignent l’âge x, de 5 ans en 5 ans, comme suit :
Etape 5 : Calcul du nombre de personnes qui atteignent le groupe d’âge x à x+4 au cours de la période située entre les deux recensements d’après les effectifs dénombrés
Le nombre de personnes qui atteignent le groupe d’âge de x à x + 4 (âge au dernier anniversaire), pendant la période de référence, se calcule en multipliant la moyenne géométrique des effectifs dénombrés dans le même groupe d’âge aux deux recensements par la durée de la période intercensitaire (mesurée en années), comme suit :
Etape 6: Calcul des rapports des estimations faites à partir des décès et des estimations faites à partir des recensements de population
On peut calculer deux séries de rapports entre les estimations qui proviennent des décès et celles qui proviennent des populations recensées. Les premiers rapports sont ceux des groupes d’âge quinquennaux, que l’on peut calculer directement. Les seconds rapports sont ceux des effectifs cumulés depuis l’âge x jusqu’à l’âge de début de l’intervalle ouvert, A, aux effectifs des personnes qui atteignent le même groupe d’âge, c'est-à-dire de l’âge x à l’âge A - 1 au cours de la période de référence, qui se calculent comme les sommes des effectifs dans les groupes d’âge quinquennaux, soit en formule :
Etape 7: Estimation de la complétude de la déclaration des décès
Afin de déterminer le niveau de sous-enregistrement des décès, il faut d’abord décider si les taux de croissance choisis doivent être corrigés pour prendre en compte la différence de couverture entre les deux recensements. L’interprétation de la représentation graphique des rapports est discutée plus en détail ci-dessous. Mais, en résumé, la correction à faire aux taux de croissance (delta) pour prendre en compte la différence de couverture entre les recensements peut se calculer comme la quantité qui produit un ensemble de rapports de même niveau, c'est-à-dire horizontaux sur le graphique. La feuille de calcul intitulée Méthode est préparée de telle manière que le module Solveur (Données / Solveur / Résoudre) trouve la valeur de delta qui minimise l’écart absolu entre la moyenne des rapports calculés sur un intervalle d’âge spécifié par l’utilisateur.
On suggère à l’analyste de commencer l’optimisation par la valeur de delta qui résulte de la méthode généralisée de la balance de l’accroissement démographique appliquée aux mêmes données. Si cette valeur initiale de delta produit un ensemble de rapports de même niveau pour les âges adultes, mais avec une courbure marquée aux âges élevés, ceci pourrait indiquer une baisse de la complétude aux âges élevés, qui pourrait être due à la désintégration de certains ménages suite au décès de l’un de ses membres. Dans ce cas, il conviendra de ne pas chercher un delta qui produise un ensemble de rapports de même niveau, mais plutôt de conserver la valeur initiale.
Lorsqu’on cherche à optimiser à la fois delta et les espérances de vie de manière itérative, les valeurs des espérances de vie devront être copiées à partir de la feuille de calcul Espérances de vie et collées dans la feuille de calcul Méthode pour rechercher une nouvelle valeur de delta. Ce processus peut être répété deux ou trois fois, jusqu’à ce que les valeurs des espérances de vie soient stables.
Finalement, on doit choisir l’intervalle d’âge sur lequel on calcule la complétude à partir des rapports. Si l’on observe une courbure marquée vers le haut aux âges élevés, on est probablement en présence d’une exagération des âges, surtout pour les décès, et il conviendra d’essayer d’identifier un âge de début de l’intervalle ouvert en dessous duquel cette exagération est négligeable. Le fait que la complétude baisse pour les âges en-dessous de 35 ans, pourrait indiquer des émigrations qui n’ont pas été prises en compte. Si l’on suspecte ce cas, il conviendra d’exclure les âges correspondants pour le calcul de delta et de la complétude.
La complétude se calcule à partir des rapports des effectifs des groupes d’âge quinquennaux. Pour obtenir un résultat assez robuste, on propose de prendre la somme pondérée comme suit : 50% de la médiane et 25% de chacun des deux quartiles (les percentiles correspondant à 25% et 75% de la distribution des rapports).
Etape 8: Calcul des taux de mortalité corrigés pour tenir compte du sous-enregistrement des décès déclarés
Pour calculer les taux de mortalité corrigés, il faut d’abord corriger le dénominateur, c'est-à-dire les effectifs de population, de la couverture relative du recensement. Si delta est négatif, ce calcul se fait en multipliant les effectifs du premier recensement pas le coefficient : , et ceux du second recensement par 1, (c’est à dire qu’ils restent inchangés); si delta est positif, on fait l’inverse, c’est à dire que le premier recensement reste inchangé et le second est multiplié par le coefficient correspondant.
Les personnes-années vécues, soit PYLa(x,5), se calculent en multipliant la moyenne géométrique des populations corrigées par la durée de la période intercensitaire (en années) comme suit :
Pour tenir compte du sous-enregistrement, on doit ensuite corriger les nombres de décès déclarés, en divisant ces nombres par l’estimation de la complétude, c. Puis on calcule les taux de mortalité corrigés en divisant les décès corrigés par les personnes-années vécues corrigées, PYLa(x,5), comme suit:
Si on pense que la complétude baisse après l’âge à la retraite, on pourra essayer d’améliorer les estimations des taux de mortalité aux âges élevés en remplaçant la valeur trouvée c par une valeur arbitraire correspondant à la complétude dans ces groupes d’âge. La feuille de calcul contient une option pour réaliser cette correction.
D’un point de vue purement technique, on pourrait ignorer la correction due à la différence de couverture des deux recensements, et trouver les mêmes taux de mortalité, car la correction est identique au numérateur et au dénominateur. Mais, dans ce cas, l’estimation de la complétude de l’enregistrement des décès par rapport à la moyenne des deux recensements ne serait plus correcte, puisqu’elle supposerait que les deux recensements ont la même couverture.
Etape 9: Lissage à l’aide d’un système relationnel logit de tables-type de mortalité
Lorsque les taux de mortalité par âge sont erratiques, on peut les lisser à l’aide d’un modèle. Ceci peut se faire à l’aide du système relationnel logit de Brass et d’une table-type du même sexe que l’on considère avoir le même schéma par âge que celui qui s’applique à la population étudiée.
Le classeur Excel correspondant à cette méthode comporte une feuille de calcul qui permet de produire des taux de mortalité lissés à l’aide d’un système relationnel logit et d’une table-type de mortalité. L’utilisateur a le choix entre un standard du modèle Général de la famille des tables-type des Nations Unies, ou l’un des quatre modèles régionaux des tables-type de Princeton. La transformation logit de ces tables-type de mortalité, ainsi qu’une table-type d’une population affectée par l’épidémie de sida (Timæus 2007) sont donnés dans la feuille de calcul Données des modèles. Cette feuille de calcul permet aussi à l’utilisateur de choisir comme standard une autre table de mortalité sous forme de logit, s’il y a de bonnes raisons de penser de cette table présente un schéma par âge similaire à celui de la population étudiée.
Pour ajuster le modèle logit, on calcule d’abord les quotients quinquennaux de mortalité, 5qx, d’après les taux corrigés de mortalité, 5mx, selon la formule :
Puis on calcule la table de mortalité de proche en proche, en partant d’une racine l5 = 1, selon la formule de récurrence suivante :
Les coefficients, α et β , du système relationnel logit se calculent par régression linéaire, comme suit:
où la fonction logit est définie comme:
et où l’exposant s désigne les valeurs de la table de mortalité de référence (le standard).
La table de mortalité lissée se calcule ensuite en appliquant les coefficients α and β comme suit :
et:
Les taux de mortalité lissés se calculent dans la table de mortalité comme suit:
et
où
soit :
où ω désigne l’âge au-delà duquel il ne reste plus de survivant.
Les espérances de vie, qui sont particulièrement importantes si l’on veut estimer les espérances de vie aux âges élevés par itération, se calculent comme suit :
Exemple
Cet exemple utilise les données de la population masculine d’Afrique du Sud, recueillies au recensement de 2001 et à l’enquête de communauté de 2007, et les données des décès enregistrés à l’état civil au cours des années de 2001 à 2007. Le solde migratoire est estimé d’après le changement du nombre de personnes nées à l’étranger repérées aux deux enquêtes, moins une estimation du nombre de sud-africains qui ont émigré à l’étranger entre les deux enquêtes. Cet exemple est détaillé dans le classeur Excel intitulé : AM_SEG_South Africa_males.
Etape 1: Puisqu’il n’est pas disponible directement, on calcule le nombre de décès déclarés au cours de la période située entre les deux estimations de population
Les décès déclarés au cours des années 2001 à 2007 pour les hommes sud-africains apparaissent dans le tableau 1.
Tableau 1 : Calcul des décès de la période intercensitaire, Afrique du sud, sexe masculin, 2001-2007
Age | 2001 | 2002–2006 | 2007 | Total entre les deux recensements |
|---|---|---|---|---|
| 0–4 | 29 005 | 186 346 | 40 314 | 197 912 |
| 5–9 | 2 118 | 14 733 | 2 854 | 15 566 |
| 10–14 | 1 745 | 10 535 | 2 233 | 11 207 |
| 15–19 | 4 470 | 23 857 | 4 860 | 25 473 |
| 20–24 | 8 931 | 51 588 | 10 875 | 54 960 |
| 25–29 | 16 834 | 96 705 | 18 405 | 102 802 |
| 30–34 | 20 892 | 137 355 | 28 245 | 145 588 |
| 35–39 | 21 068 | 137 502 | 29 258 | 145 900 |
| 40–44 | 19 322 | 128 217 | 26 973 | 135 936 |
| 45–49 | 17 881 | 113 891 | 24 761 | 121 010 |
| 50–54 | 16 883 | 104 508 | 22 790 | 111 157 |
| 55–59 | 14 544 | 90 919 | 21 317 | 96 854 |
| 60–64 | 15 097 | 84 351 | 17 410 | 89 930 |
| 65–69 | 13 011 | 77 680 | 17 878 | 82 843 |
| 70–74 | 14 035 | 68 147 | 13 771 | 73 036 |
| 75–79 | 10 846 | 59 859 | 12 534 | 63 871 |
| 80–84 | 9 161 | 44 986 | 8 872 | 48 163 |
| 85+ | 7 602 | 43 233 | 10 009 | 46 196 |
La date de référence du recensement de 2001 était la nuit du 9 au 10 octobre 2001. L’enquête de communauté se déroula sur plusieurs semaines en février, et on prendra comme date de référence la nuit du 14 au 15 février 2007. Donc, en supposant que les décès sont répartis uniformément au cours de l’année, on peut répartir proportionnellement les décès de 2001 et de 2007, et les ajouter au total des années 2002 à 2006. Ceci donne le total des décès qui se sont produits entre les deux dates de recensement. Par exemple, pour le groupe d’âge 20-24 ans, le nombre se calcule comme suit :
Etape 2 : Calcul des taux de croissance, après correction pour les migrations et pour la différence de couverture entre les deux recensements
Les taux de croissance par âge se calculent en soustrayant les taux de migrations nettes, et après correction pour tenir compte de la différence de couverture des deux recensements : ils sont présentés en colonne 6 du tableau 2. Par exemple, pour le groupe d’âge de 20-24 ans, les effectifs de population apparaissent en colonnes 2 et 3, les migrations nettes en colonne 5 du tableau 2, et avec un delta estimé plus loin, on trouve :
où 5,3541 correspond à la durée de la période intercensitaires, calculée par la fonction YEARFRAC du logiciel Excel.
Tableau 2 : Taux de croissance par âge, et effectifs des personnes qui atteignent l’âge x, et qui atteignent le groupe d’âge x à x+5, calculés d’après le nombre de décès déclarés, Afrique du sud, sexe masculin, 2001-2007
| Age | 5Nx(t1) | 5Nx(t2) | 5Dx | 5NMx | 5rx | Est Nx | Est 5Nx | ||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 2 223 006 | 2 505 744 | 197 912 | 10 605 | 0,0168 | ||||
| 5 | 2 425 066 | 2 560 642 | 15 566 | 2 848 | 0,0053 | 2 304 653 | 11 334 968 | ||
| 10 | 2 518 985 | 2 452 339 | 11 207 | 5 153 | -0,0101 | 2 229 335 | 11 405 753 | ||
| 15 | 2 453 156 | 2 553 293 | 25 473 | 16 574 | 0,0016 | 2 332 967 | 11 556 063 | ||
| 20 | 2 099 417 | 2 362 519 | 54 960 | 14 803 | 0,0161 | 2 289 459 | 10 871 687 | ||
| 25 | 1 899 275 | 2 033 165 | 102 802 | 4 714 | 0,0076 | 2 059 216 | 9 851 950 | ||
| 30 | 1 594 624 | 1 875 483 | 145 588 | 13 331 | 0,0242 | 1 881 564 | 8 529 425 | ||
| 35 | 1 441 657 | 1 548 185 | 145 900 | 9 693 | 0,0074 | 1 530 206 | 7 153 512 | ||
| 40 | 1 233 813 | 1 306 900 | 135 936 | 7 464 | 0,0050 | 1 331 199 | 6 238 580 | ||
| 45 | 967 744 | 1 104 294 | 121 010 | 8 719 | 0,0184 | 1 164 233 | 5 276 384 | ||
| 50 | 769 627 | 888 042 | 111 157 | 9 413 | 0,0199 | 946 320 | 4 242 847 | ||
| 55 | 552 402 | 708 812 | 96 854 | 4 640 | 0,0405 | 750 818 | 3 191 145 | ||
| 60 | 444 592 | 491 871 | 89 930 | 5 081 | 0,0122 | 525 640 | 2 332 526 | ||
| 65 | 304 835 | 394 305 | 82 843 | 4 922 | 0,0407 | 407 371 | 1 662 114 | ||
| 70 | 232 604 | 241 976 | 73 036 | 4 334 | -0,0007 | 257 475 | 1 106 744 | ||
| 75 | 136 466 | 163 112 | 63 871 | 2 980 | 0,0249 | 185 223 | 721 856 | ||
| 80 | 90 856 | 87 698 | 48 163 | 1 662 | -0,0148 | 103 519 | 412 486 | ||
| 85 | 45,920 | 70,299 | 46,196 | 2,009 | 0.0683 | 61,475 | |||
Etape 3: Estimation de l’espérance de vie à l’âge A et aux anniversaires correspondants aux débuts des groupes d’âge quinquennaux, jusqu’à 65 ans
Les estimations provenant de l’application de la méthode généralisée de la balance de l’accroissement démographique en utilisant les mêmes données apparaissent en colonne 2 du tableau 3.
Le rapport des décès déclarés dans les groupes d’âge 10-39 ans et 40-59 ans (âge au dernier anniversaire), dont les données figurent en colonne 4 du tableau 2, se calcule comme suit :
Ce rapport sert pour entrer dans le système de tables-type de mortalité du modèle Ouest de Princeton (on trouve le tableau dans la feuille de calcul Espérances de vie du classeur Excel). La table correspondante est identifiée par interpolation, et les espérances de vie correspondantes apparaissent en colonne 3 du tableau 3. Par exemple, pour l’espérance de vie à 65 ans :
En partant de ces valeurs de la table-type du modèle Ouest, on peut procéder par itération, et calculer l’espérance de vie et delta (comme cela est expliqué plus en détail ci-dessous). On trouve alors une valeur de delta = -0,0066, et les estimations de l’espérance de vie apparaissent en colonne 4 du tableau 3.
Tableau 3 : Espérances de vie calculées selon diverses méthodes, Afrique du sud, sexe masculin, 2001-2007
x | Méthode généralisée de la balance de l’accroissement démographique | Table-type du modèle Ouest de Princeton | Itérations successives | Delta déterminé par la méthode généralisée de la balance de l’accroissement démographique |
|---|---|---|---|---|
65 | 11,7 | 9,45 | 11,6 | 11,7 |
70 | 9,4 | 7,37 | 9,3 | 9,4 |
75 | 7,4 | 5,55 | 7,3 | 7,4 |
80 | 5,7 | 4,06 | 5,6 | 5,7 |
85 | 4,4 | 2,90 | 4,3 | 4,4 |
Comme la prévalence du VIH est élevée en Afrique du sud, on ne peut pas utiliser les estimations provenant de la table-type du modèle Ouest, qui sont fournies par la feuille de calcul Espérances de vie du classeur Excel correspondant. De plus, comme cela est discuté plus loin, il semble que la complétude tende à baisser avec l’âge au-delà de 55 ans, et donc la procédure par itération s’applique probablement mal. Donc, dans cet exemple, on choisira une valeur de delta égale à l’ordonnée à l’origine obtenue par la Méthode généralisée de la balance de l’accroissement démographique, appliquée aux mêmes données. Les résultats apparaissent en colonne 5 du tableau 3.
Etape 4 : Estimation du nombre de personnes qui atteignent l’âge x et le groupe d’âge x à x+4, (âge au dernier anniversaire) d’après les décès déclarés
Le nombre de personnes qui atteignent l’âge x (leur x-ème anniversaire) entre les deux recensements se calcule à partir du nombre de décès déclarés, en prenant comme intervalle d’âge ouvert 85 ans et plus, les taux de croissance qui figurent en colonne 6 du tableau 2, et l’estimation de l’espérance de vie à 85 ans (4,347 ans) qui figure en colonne 5 du tableau 3. Les résultats apparaissent en colonne 7 du tableau 2. Par exemple, le nombre de personnes qui atteignent 80 ans au cours de la période intercensitaire se calcule comme suit, en prenant le taux de croissance de +0,0638 dans le groupe d’âge 85 ans et plus, et de -0,0148 dans le groupe d’âge 80-85 ans :
Le nombre de personnes qui atteignent le groupe d’âge de x à x + 4 (âge au dernier anniversaire) pendant la période intercensitaire, se calcule d’après les décès déclarés, et apparaît en colonne 8 du tableau 2. Par exemple, le nombre de personnes qui atteignent le groupe d’âge 20-24 ans se calcule comme suit :
Etape 5 : Estimation du nombre de personnes qui atteignent le groupe d’âge x à x+4, (âge au dernier anniversaire) d’après les données du recensement
Le nombre de personnes qui atteignent le groupe d’âge x à x+4 au cours de la période intercensitaire apparaît en colonne 2 du tableau 4. Pour le groupe d’âge de 20-24 ans, par exemple, il se calcule à partir des populations données en colonnes 2 et 3 du tableau 2, et de la durée entre les deux recensements, comme suit :
Tableau 4 : Nombre de personnes qui atteignent le groupe d’âge x à x+4, calculé d’après les recensements de population; et ratios des estimations faites à partir des décès et à partir des populations, Afrique du sud, sexe masculin, 2001-2007
Age | Obs 5Nx | c: 5Nx | c: A–xNx |
|---|---|---|---|
| 0 | 12 636 377 | ||
| 5 | 13 341 976 | 0,8496 | 0,8981 |
| 10 | 13 307 209 | 0,8571 | 0,9050 |
| 20 | 11 923 972 | 0,9118 | 0,9231 |
| 25 | 10 521 174 | 0,9364 | 0,9256 |
| 30 | 9 259 118 | 0,9212 | 0,9230 |
| 35 | 7 998 828 | 0,8943 | 0,9235 |
| 40 | 6 798 761 | 0,9176 | 0,9322 |
| 45 | 5 534 858 | 0,9533 | 0,9371 |
| 50 | 4 426 301 | 0,9586 | 0,9310 |
| 55 | 3 350 250 | 0,9525 | 0,9191 |
| 60 | 2 503 746 | 0,9316 | 0,9028 |
| 65 | 1 856 232 | 0,8954 | 0,8865 |
| 70 | 1 270 220 | 0,8713 | 0,8799 |
| 75 | 798 803 | 0,9037 | 0,8885 |
| 80 | 477 921 | 0,8631 | 0,8631 |
Etape 6 : Calcul des rapports des estimations faites à partir des décès aux estimations faites à partir des recensements
Les rapports des estimations des personnes qui atteignent le groupe d’âge x à x + 4 au-cours de la période intercensitaire faites à partir des décès (colonne 8 du tableau 2) et à partir des populations (colonne 2 du tableau 4) apparaissent en colonnes 3 et 4 du tableau 4. Par exemple pour les groupes d’âge de 60-64 ans, et de 65-84 ans, les calculs se font comme suit :
Etape 7 : Estimation de la complétude de l’enregistrement des décès
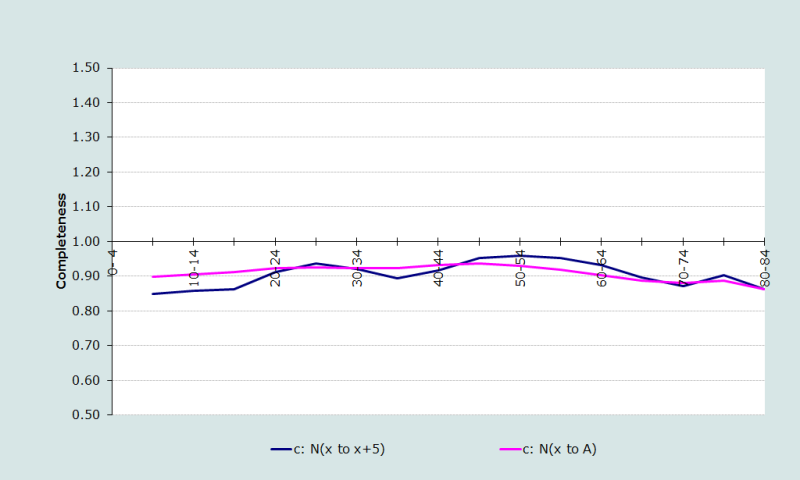
En prenant comme delta la valeur de l’ordonnée à l’origine obtenue en appliquant la méthode généralisée de la balance de l’accroissement démographique, on obtient une série de rapports qui sont d’un niveau assez stable, mais qui semblent baisser un peu au-delà de l’âge de 50 ans (voir la figure 1). Donc, dans cet exemple, on n’a pas utilisé l’optimisation avec le module Solveur pour calculer delta.
On propose ici d’estimer la complétude à partir des rapports calculés entre les âges de 25 à 64 ans. On fait ce choix pour éviter, dans une certaine mesure, de biaiser l’estimation vers le bas que l’on aurait si on utilisait les rapports aux âges élevés, même si la méthode utilisée est assez robuste aux variations des rapports dans les groupes d’âges quinquennaux. Ce choix donne une estimation de la complétude de 94%, qui se calcule comme suit :
où 0,9340 est la médiane, 0,9203 le premier quartile, et 0,9527 le troisième quartile des rapports calculés en colonne 3 du tableau 4, pour les âges de 25 à 65 ans.
Etape 8 : Estimation des taux de mortalité corrigés pour tenir compte du sous-enregistrement des décès
La population corrigée à la date du premier recensement qui apparaît en colonne 2 du tableau 5, est égale à la population effectivement recensée (colonne 2 du tableau 2), multipliée par le coefficient :
exp(‑(‑0,00467) x 5,3541), puisque delta est inférieur à 0. Par exemple, pour le groupe d’âge 20-24 ans le calcul de la population corrigée se fait comme suit:
La population corrigée à la date du second recensement qui apparaît en colonne 3 du tableau 5, est égale à la population effectivement recensée (colonne 3 du tableau 2), puisque delta est inférieur à 0.
Ensuite, on calcule les décès corrigés pour tenir compte du sous-enregistrement en divisant le nombre de décès déclarés dans chaque groupe d’âge (colonne 4 du tableau 2) par l’estimation de la complétude. Les résultats apparaissent en colonne 4 du tableau 5. Par exemple, pour le groupe d’âge 20-24 ans, le nombre corrigé s’obtient à partir du nombre observé (54 960 décès), comme suit :
Comme il semble que la complétude ait tendance à baisser aux âges élevés, on choisit d’utiliser une complétude qui diffère par âge au-delà de 65 ans. Ainsi, par exemple pour le groupe d’âge 70-74 ans, on prend une nouvelle complétude (0,8713), et on obtient :
Les personnes-années vécues corrigées (colonne 5 du tableau 5) se calculent comme la moyenne géométrique des populations figurant en colonnes 2 et 3 du tableau 5, multiplié par la durée de la période intercensitaire (exprimée en années), qui dans ce cas est égale à 5,3541 années. Par exemple, pour le groupe d’âge 20-24 ans, le calcul se fait comme suit :
Les taux de mortalité corrigés, pour tenir compte à la fois du sous-enregistrement des décès et de la différence de couverture entre les recensements (colonne 6 du tableau 5) se calculent selon la formule classique, en divisant les décès corrigés par les personnes-années vécues corrigées. Par exemple, pour le groupe d’âge 20-24 ans, le taux de mortalité corrigé se calcule comme suit :
Tableau 5 Calcul des taux corrigés de mortalité, Afrique du sud, sexe masculin, 2001-2007
Age | Données corrigées | ||||
|---|---|---|---|---|---|
| 5Nx(t1) | 5Nx(t2) | 5Dx | PYL(x,5) | 5mx | |
| 0 | |||||
| 5 | 2 486 532 | 2 560 642 | 16 644 | 13 510 001 | 0,0012 |
| 10 | 2 582 831 | 2 452 339 | 11 983 | 13 474 797 | 0,0009 |
| 15 | 2 515 334 | 2 553 293 | 27 236 | 13 568 508 | 0,0020 |
| 20 | 2 152 629 | 2 362 519 | 58 764 | 12 074 140 | 0,0049 |
| 25 | 1 947 414 | 2 033 165 | 109 919 | 10 653 675 | 0,0103 |
| 30 | 1 635 041 | 1 875 483 | 155 667 | 9 375 725 | 0,0166 |
| 35 | 1 478 197 | 1 548 185 | 156 001 | 8 099 564 | 0,0193 |
| 40 | 1 265 085 | 1 306 900 | 145 347 | 6 884 383 | 0,0211 |
| 45 | 992 273 | 1 104 294 | 129 387 | 5 604 563 | 0,0231 |
| 50 | 789 134 | 888 042 | 118 852 | 4 482 045 | 0,0265 |
| 55 | 566 403 | 708 812 | 103 560 | 3 392 442 | 0,0305 |
| 60 | 455 861 | 491 871 | 96 156 | 2 535 277 | 0,0379 |
| 65 | 312 561 | 394 305 | 92 518 | 1 879 609 | 0,0492 |
| 70 | 238 500 | 241 976 | 83 824 | 1 286 217 | 0,0652 |
| 75 | 139 925 | 163 112 | 70 679 | 808 863 | 0,0874 |
| 80 | 93 159 | 87 698 | 55 803 | 483 940 | 0,1153 |
| 85 | 47 084 | 70 299 | 53 524 | 308 032 | 0,1738 |
Etape 9 : Lissage en utilisant un système relationnel logit associé à une table-type
On peut dès lors calculer les quotients de mortalité quinquennaux corrigés, 5qx, à partir des taux de moralité corrigés (colonne 6 du tableau 5) et qui apparaissent en colonne 2 du tableau 6. Par exemple, la probabilité pour une femme de décéder entre 20 et 25 ans se calcule comme suit :
On dérive de proche en proche les survivants de la table de mortalité, de 5 ans en 5 ans, selon la formule classique qui lie les survivants à l’âge x+5 aux survivants à l’âge x (colonne 3 du tableau 6). Par exemple, les survivants à 25 ans se calculent comme suit :
Tableau 6 : Calcul de la table de mortalité conditionnelle, lissée à l’aide du système relationnel logit et d’une table-type de mortalité, Afrique du sud, sexe masculin, 2001-2007
Age | 5qx | lx/l | Y(x) | Sida | Logit | Logit | Surviv. | T(x) | e(x) | Taux lissé 5mx |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | ||||||||||
5 | 0,0061 | 1 |
| 1,0000 |
|
| 1 | 51,206 | 51,2 | 0,0030 |
10 | 0,0044 | 0,9939 | -2,5433 | 0,9785 | -1,9081 | -2,0984 | 0,9852 | 46,243 | 46,9 | 0,0028 |
15 | 0,0100 | 0,9894 | -2,2705 | 0,9632 | -1,6326 | -1,7676 | 0,9717 | 41,351 | 42,6 | 0,0024 |
20 | 0,0240 | 0,9796 | -1,9350 | 0,9512 | -1,4853 | -1,5907 | 0,9601 | 36,521 | 38,0 | 0,0041 |
25 | 0,0503 | 0,9560 | -1,5395 | 0,9324 | -1,3120 | -1,3827 | 0,9408 | 31,769 | 33,8 | 0,0086 |
30 | 0,0797 | 0,9079 | -1,1444 | 0,8969 | -1,0818 | -1,1062 | 0,9014 | 27,164 | 30,1 | 0,0152 |
35 | 0,0919 | 0,8356 | -0,8128 | 0,8420 | -0,8365 | -0,8116 | 0,8352 | 22,822 | 27,3 | 0,0200 |
40 | 0,1003 | 0,7588 | -0,5731 | 0,7794 | -0,6311 | -0,5650 | 0,7559 | 18,845 | 24,9 | 0,0235 |
45 | 0,1091 | 0,6827 | -0,3831 | 0,7148 | -0,4593 | -0,3588 | 0,6721 | 15,275 | 22,7 | 0,0239 |
50 | 0,1243 | 0,6082 | -0,2199 | 0,6560 | -0,3228 | -0,1948 | 0,5962 | 12,104 | 20,3 | 0,0230 |
55 | 0,1418 | 0,5326 | -0,0653 | 0,6048 | -0,2127 | -0,0626 | 0,5313 | 9,285 | 17,5 | 0,0255 |
60 | 0,1732 | 0,4571 | 0,0861 | 0,5530 | -0,1064 | 0,0650 | 0,4676 | 6,788 | 14,5 | 0,0335 |
65 | 0,2191 | 0,3779 | 0,2493 | 0,4918 | 0,0163 | 0,2124 | 0,3954 | 4,631 | 11,7 | 0,0502 |
70 | 0,2802 | 0,2951 | 0,4354 | 0,4119 | 0,1781 | 0,4066 | 0,3072 | 2,874 | 9,4 | 0,0718 |
75 | 0,3586 | 0,2124 | 0,6553 | 0,3178 | 0,3819 | 0,6513 | 0,2137 | 1,572 | 7,4 | 0,1013 |
80 | 0,4475 | 0,1362 | 0,9235 | 0,2173 | 0,6408 | 0,9622 | 0,1274 | 0,719 | 5,6 | 0,1480 |
85 | #N/A | 0,0753 | 1,2542 | 0,1201 | 0,9959 | 1,3887 | 0,0586 | 0,255 | 4,3 | 0,2097 |
La transformation logit appliquée aux proportions de survivants figure en colonne 4 du tableau 6. Par exemple, à l’âge de 20 ans, le logit de l20 se calcule comme suit :
Dans la table de mortalité conditionnelle pour le sexe masculin, la transformation logit est appliquée aux proportions de survivants de la table-type spéciale qui tient compte du sida, avec une espérance de vie e0 = 50 (colonne 5 du tableau 6); les résultats apparaissent en colonne 6 du tableau 6. Comme on peut le voir sur la figure 2, la table-type qui tient compte du sida n’ajuste pas bien les données, mais elle marche mieux que toute autre table-type qui ne tient pas compte de l’impact du sida sur la mortalité.

Les coefficients, α et β, sont déterminés comme la pente et l’ordonnée à l’origine de la droite qui ajuste au mieux les transformations logits, qui figurent en colonnes 4 et 6 du tableau 6, dans l’intervalle d’âge choisi par l’utilisateur (entre 45 et 80 ans dans cet exemple), soit ici 0,1928 et 1,2008 respectivement.
On applique ensuite ces coefficients aux logits de la table de mortalité conditionnelle, afin de produire les logits lissés (colonne 7 du tableau 6). Par exemple, pour l’âge de 20 ans, le logit lissé se calcule comme suit :
Ces valeurs sont ensuite prises pour calculer la table de mortalité lissée (colonne 8 du tableau 6). Par exemple, la probabilité de survie à 20 ans se calcule comme suit :
Les personnes-années vécues cumulées au-delà de l’âge x, soit Tx, figurent en colonne 9 du tableau 6, et se calculent à partir de la table de mortalité lissée. Ces valeurs sont alors utilisées pour calculer les taux de mortalité lissés, qui figurent en colonne 10 du tableau 6. Par exemple, à l’âge de 80 ans :
Les espérances de vie, qui apparaissent en colonne 10 du tableau 6, se calculent selon la formule classique, en divisant les Tx, qui figurent en colonne 9, par les lx, qui figurent en colonne 8 du tableau 6. Par exemple, l’espérance de vie à 65 ans se calcule comme suit :
Diagnostics, analyse et interprétation
Contrôles et validation
L’estimation de la complétude est de 94%. La première vérification à faire sur ce résultat est la comparaison avec le résultat correspondant pour l’autre sexe. Ainsi, en appliquant la même méthode que pour les hommes aux données concernant les femmes au cours de la même période (voir la feuille de calcul : AM_SEG_South Africa_females) donne une estimation de la complétude de 93%. Des recherches antérieures (Dorrington, Moultrie and Timæus 2004) ont montré que l’on peut s’attendre à des résultats voisins pour les deux sexes, et le fait que ces résultats le sont en effet valide par conséquent ces estimations
Une seconde vérification des résultats consiste à les comparer avec ceux obtenus par la Méthode généralisée de la balance de l’accroissement démographique (voir la feuille de calcul : AM_GGB_South Africa_males). Cette méthode donne une estimation de la complétude de 92% sur l’intervalle d’âge de 5 à 84 ans, ce qui aussi suffisamment proche pour valider les résultats précédents
Une troisième vérification consiste à comparer diverses estimations de la mortalité avec d’autres sources, telles que des estimations antérieures pour le pays, ou les ‘Perspectives de la population mondiale’ (UN Population Division 2011). L’estimation du quotient de mortalité de 15 à 60 ans, 45q15, est de 519 pour 1000 après correction pour tenir compte de la sous-déclaration, une valeur proche des 529 pour 1000 retenue par les ‘Perspectives de la population mondiale’ pour la période 2000-2005, ce qui une fois encore montre qu’il y a peu de raisons de mettre en question les résultats obtenus par la méthode.
Il est intéressant de remarquer que l’application de la Méthode de Preston et Coale à ces mêmes données, en prenant pour population moyenne la population au milieu de l’intervalle entre les deux recensements, donne une estimation de 84% lorsqu’on utilise le même intervalle d’âge. Si on augmente l’âge minimal à 35 ans pour calculer delta, on augmente l’estimation à 86%, toujours un peu plus faible que l’estimation de 94% produite par la méthode utilisée ci-dessus.
Interprétation
L’analyse des estimations de la complétude (voir la figure 1) suggère que la complétude de l’enregistrement des décès semble assez peu variable selon l’âge, du moins au-delà de l’âge de 50 ans. Cette observation est cohérente avec le fait que de nombreux travailleurs migrent aux âges de la retraite des zones urbaines vers les zones rurales, là où la déclaration des décès est plus faible. Comme ces estimations de la complétude sont produites avec un delta qui provient de l’application de la méthode généralisée de la balance de l’accroissement démographique, et qu’il est très vraisemblable que nombre de personnes ont effectivement migré de l’urbain vers le rural, réduire la valeur de delta pour obtenir des niveaux plus réguliers ne serait pas approprié dans ce cas.
Comme on a déjà pris en compte les migrations, la baisse de l’estimation de la complétude aux jeunes âges est probablement due à l’effet contraire de celui qui se produit aux âges élevés : les jeunes adultes migrent des zones rurales vers les zones urbaines, pour y trouver un emploi. Il serait donc erroné de laisser les estimations correspondant aux âges de ces jeunes adultes influencer l’estimation finale de la complétude.
Les irrégularités visibles dans la série des rapports des effectifs, , provient des populations au recensement et à l’enquête de communauté, et non des décès. Le caractère erratique de cette série indique probablement des erreurs dans les décomptes de certains groupes d’âge ou bien des erreurs sur les âges dans les populations du recensement ou de l’enquête.
Problèmes d’interprétation specifiques de la methode
Source des données sur les décès déclarés
On trouve en général deux types de problèmes avec les données concernant les décès : ceux qui conduisent à un biais de déclaration (sous- ou sur-déclaration) qui est constant par âge, ce qui est précisément ce que la méthode vise à corriger, et ceux qui conduisent à des biais de déclaration qui varient selon l’âge, qui peuvent entraîner une distorsion dans les estimations finales. Bien que l’approche générale reste essentiellement la même quelle que soit la source des données, des sources différentes peuvent être sujettes à des biais spécifiques, qui peuvent avoir un effet sur l’interprétation des résultats. On va illustrer ces cas par des exemples concrets, et d’une manière générale, l’analyse devra prêter attention aux biais suivants dans les données concernant les décès.
1) Décès déclarés à l’état civil
Si la répartition de la population entre les zones urbaines et rurales (ou une division équivalente) diffère significativement par âge, et que la complétude de la déclaration des décès en milieu urbain est significativement supérieure à celle du milieu rural, alors l’hypothèse selon laquelle la complétude est indépendante de l’âge sera vraisemblablement violée, et la complétude va tendre à baisser avec l’âge au-delà de 50 ans si la proportion de personnes qui migrent de l’urbain vers le rural au moment de leur retraite. Si on l’ignore, cette violation de l’hypothèse produira probablement une sous-estimation du niveau moyen de la complétude.
2) Décès déclarés par les ménages
Ces données sont sujettes à quatre problèmes potentiels :
- Si une proportion significative de ménages sont dissous après le décès d’une personne clé (comme la seule personne à subvenir aux besoins du ménage), alors le décès de cette personne risque de ne pas être déclaré, ce qui conduit à violer l’hypothèse que la complétude est constante selon l’âge. Si une proportion significative de décès dans certains groupes d’âge concerne des individus qui ne vivent pas dans des ménages ordinaires (par exemple, ceux qui vivent dans des maisons pour personnes âgées), la violation de l’hypothèse peut même être encore plus sévère. Mais ce n’est pas encore un problème dans la plupart des pays en développement.
- Dans les situations où les jeunes adultes quittent leur famille lorsqu’ils grandissent, pour aller vivre en ville, il est possible qu’ils soient considérés comme membres de plusieurs ménages (ou d’aucun ménage), et leurs décès peuvent être déclarés plus d’une fois (ou jamais), ce qui conduit encore à une violation de l’hypothèse de déclaration des décès constante selon l’âge. Dans ce cas, on peut en limiter l’impact en ignorant les données concernant les décès d’âge inférieur à un âge donné pour estimer la complétude.
- Erreurs sur la période de référence. Comme il arrive fréquemment qu’il y ait confusion sur la période précise au cours de laquelle on doit déclarer les décès, sans même parler d’erreurs sur la date précise du décès, il est possible que cela se traduise par soit une sous-déclaration, soit une sur-déclaration des décès. En supposant que l’on puisse faire l’hypothèse que ces biais sont indépendants de l’âge des décédés, cette distorsion sera prise en compte dans l’estimation de la complétude, et ne constituera pas un problème pour le calcul des taux de mortalité corrigés.
- La période de référence ne couvre qu’une petite partie de la période intercensitaire. Par exemple, on demande fréquemment aux ménages de déclarer les décès qui ont eu lieu au cours des 12 derniers mois précédant le recensement. Non seulement une période très courte comme celle-ci produit de fortes fluctuations aléatoires, mais de plus cela pose le problème supplémentaire de l’estimation de la population au début de cette période de référence. On illustrera ce point dans les exemples ci-dessous, et on expliquera comment résoudre le problème. Par contre, si l’on dispose en plus des décès déclarés par les ménages au premier recensement, on peut utiliser les deux ensembles de données sur les décès pour estimer le nombre de décès qui se sont produits entre les deux recensements, comme cela a été expliqué ci-dessus. Toutefois, comme la question relative aux décès des 12 derniers mois au sein des ménages n’a été posée que relativement peu fréquemment avant le cycle des recensements des années 2010, il se peut que l’on ait un seul ensemble de données sur les décès. Dans ce cas, s’il n’y a pas de raison de présumer que le schéma par âge de mortalité ait changé rapidement au cours de la période, on recommande de calculer les taux de mortalité par âge pour l’année concernée, et d’appliquer ces taux aux personnes-années vécues au cours de l’intervalle intercensitaire, de manière à obtenir une estimation des décès au cours de la période. Mais si on a de bonnes raisons de penser que la mortalité a changé rapidement, par exemple du fait de l’épidémie de VIH/sida, alors cette adaptation va vraisemblablement biaiser les résultats, soit en sous-estimant, soit en surestimant la mortalité, et dans ce cas on ne recommande pas d’utiliser cette méthode de répartition des décès.
3) Décès enregistrés dans les centres de santé
On sait peu de choses à propos de cette source de données, ni comment elle fonctionne. On peut cependant supposer que la complétude dépendra de la répartition géographique des centres de santé auprès desquels les données seront collectées. Dans de nombreux pays en développement, ce genre de services a tendance à être concentré dans les zones urbaines. Dans ce cas, une nouvelle fois, si la proportion de la population vivant en milieu urbain plutôt qu’en milieu rural varie selon l’âge, on ne pourra pas supposer que la complétude est indépendante de l’âge. Il est aussi possible que certaines causes de décès soient plus fréquentes dans les centres de santé, et que si ces causes sont importantes en nombre et qu’elles sont liées à l’âge, tout ceci pourra entrainer une nouvelle violation de l’hypothèse de la complétude constante selon l’âge.
Dans tous les cas mentionnés ci-dessus, on devrait résister à la tentation d’ajuster delta de manière à obtenir une série de rapports de même niveau, et on devrait plutôt s’assurer que l’estimation de c est calculée à partir d’un intervalle d’âges qui exclut les âges où l’on observe les distorsions.
Interprétation diagnostique générale
En pratique, les deux séries des rapports et sont susceptibles d’être affectées par des violations des diverses hypothèses. Mais une des forces de cette méthode est que la plupart des violations des hypothèses produit des déviations caractéristiques et distinctes du schéma attendu de points alignés horizontalement, et dans certaines circonstances ces déviations peuvent être interprétées. En voici quelques exemples :
Estimation erronée de la couverture des recensements. Lorsque delta est trop élevé, la séquence des points est assez linéaire, mais elle tend à augmenter avec l’âge vers le niveau sous-jacent de complétude, et vice-versa, comme on peut s’y attendre d’après l’équation 1 présentée ci-dessous. L’effet est plus fort pour que pour .
- Exagération de l’âge déclaré. Il est fréquent que les proches des défunts qui déclarent les décès exagèrent l’âge des décédés, plus que ne le font les personnes vivantes déclarant leur propre âge au recensement. Ce biais produit une séquence de point d’abord régulière, mais qui tend à augmenter rapidement au-delà de l’âge auquel se produit l’exagération. D’après l’équation 1 présentée ci-dessous, l’exagération de l’âge tend à augmenter le nombre de décès aux âges élevés. De plus, les transferts entre les groupes d’âge font que le nombre de décès est multiplié par un coefficient exponentiel qui est plus fort, même si ce second effet a beaucoup moins d’impact. En théorie, un tel biais pourrait aussi être produit par une augmentation de la complétude avec l’âge, au-delà d’un certain âge, mais ce cas ne se produit pas en pratique (Preston, Coale, Trussell et al. 1980).
- Erreurs sur l’âge au recensement, et couverture variable selon l’âge. Quand ces phénomènes se produisent, on observe une séquence irrégulière des rapports dans l’intervalle d’âge considéré. Comme les effectifs sont de nature cumulative, ils tendent à suivre d’assez près la répartition par âge de la population. Ainsi donc, si on observe des zigzags, il est vraisemblable que les pics soient associés à une surestimation de la population, et les baisses à une sous-estimation. Si ces fluctuations sont indépendantes de l’âge, elles n’introduiront pas de distorsion notable dans les estimations de la complétude. Par contre si elles sont systématiques, par exemple du fait de migrations non-prises en compte en-dessous d’un certain âge, il pourrait être souhaitable d’exclure ces points lors de l’estimation finale de la complétude.
Exemples tires des décès déclares au sein des ménages lors d’un recensement ou d’une enquete
Les exemples décrits ci-dessous utilisent les mêmes données que celles qui sont utilisées dans les classeurs Excel suivants : AM_SEG_South Africa_males et AM_SEG_South Africa_females. Mais, au lieu d’utiliser les données des décès déclarés à l’état civil, on partira des décès des 12 derniers mois déclarés au sein des ménages au recensement de 2001 et à l’enquête de communauté de 2007. Ces nombres de décès apparaissent dans le tableau 7.
Tableau 7 : Décès des 12 derniers mois déclarés au sein des ménages enquêtés au recensement de 2001 et à l’enquête de communauté de 2007, Afrique du sud
| Recensement, 2001 | Enquête de communauté, 2007 | |||
|---|---|---|---|---|
| Age | Sexe masculin | Sexe féminin | Sexe masculin | Sexe féminin |
| 0-4 | 35 873 | 32 096 | 48 322 | 44 418 |
| 5-9 | 3 868 | 3 155 | 4 505 | 5 216 |
| 10-14 | 2 590 | 2 284 | 3 442 | 3 259 |
| 15-19 | 5 628 | 5 122 | 8 246 | 7 878 |
| 20-24 | 10 976 | 13 246 | 16 360 | 21 702 |
| 25-29 | 17 787 | 19 727 | 27 551 | 35 840 |
| 30-34 | 20 038 | 18 292 | 34 832 | 42 576 |
| 35-39 | 19 816 | 15 521 | 38 061 | 34 809 |
| 40-44 | 17 417 | 12 124 | 33 604 | 28 823 |
| 45-49 | 15 840 | 10 105 | 27 829 | 20 973 |
| 50-54 | 15 077 | 9 144 | 28 223 | 18 891 |
| 55-59 | 12 781 | 7 755 | 22 868 | 13 118 |
| 60-64 | 13 428 | 10 367 | 18 775 | 14 912 |
| 65-69 | 11 820 | 10 195 | 17 532 | 14 298 |
| 70-74 | 11 885 | 10 809 | 14 879 | 14 645 |
| 75-79 | 8 794 | 8 393 | 12 966 | 14 151 |
| 80-84 | 7 484 | 9 371 | 9 204 | 12 063 |
| 85+ | 7 115 | 12 389 | 11 735 | 18 178 |
Les nombres de décès qui se sont produits entre la date moyenne du premier recensement (la nuit du 9 au 10 octobre 2001) et la date moyenne de l’enquête de communauté (considérée être la nuit du 14 au 15 février 2007) se calculent en utilisant les classeurs Excel suivants : AM_Estimating deaths_South Africa_males_hhd et AM_Estimating deaths_South Africa_females_hhd.
L’application de la méthode de l’extinction des cohortes synthétiques aux mêmes données concernant le sexe masculin, et en utilisant comme estimation de la couverture relative des recensements, delta, celle fournie par la méthode généralisée de la balance de l’accroissement démographique appliquée aux même données, que l’on peut trouver dans le classeur Excel AM_SEG_South Africa_males_hhd, suggère que le décompte des décès des 12 dernier mois est pratiquement aussi complet que celui de l’état civil. Cependant, les données relatives aux décès des 12 derniers mois donnent un quotient de mortalité de 15 à 60 ans, 45q15 , égal à 539 pour mille, qui est légèrement supérieur à celui obtenu à partir des données de l’état civil, même s’il reste très proche.
L’application de la méthode de l’extinction des cohortes synthétiques aux mêmes données concernant le sexe féminin, que l’on peut trouver dans le classeur Excel AM_SEG_South Africa_females_hhd, suggère que le décompte des décès des 12 dernier mois est nettement moins fiable que celui de l’état civil. Les données des 12 derniers mois donnent un quotient de mortalité de 15 à 60 ans, 45q15 , égal à 493 pour mille, qui est nettement supérieur à celui obtenu à partir des données de l’état civil (420 pour 1000), et moins plausible si on le compare au quotient équivalent pour les hommes.
Les raisons de cette performance plus médiocre de la méthode lorsqu’elle est appliquée aux décès féminins déclarés au sein des ménages peuvent être recherchées dans la comparaison des nombres de décès déclarés par au sein des ménages avec les données de l’état civil après correction pour tenir compte du sous-enregistrement, comme cela apparaît dans le tableau 8. On peut y voir que le nombre de décès féminins déclarés par les ménages est nettement inférieur à celui de l’état civil au-delà de l’âge de 55 ans, probablement du fait de la dissolution des ménages suite à leurs décès, car beaucoup de ces ménages ont pour chef une femme âgée, susceptible de décéder. On peut aussi y voir une sur-déclaration des décès des hommes de moins de 30 ans et des femmes de moins de 25 ans, ou peut-être une sous-déclaration de ces décès à l’état civil.
Tableau 8 : Rapport des décès des 12 derniers mois déclarés au sein des ménages aux estimations attendues des décès déclarés à l’état civil après correction pour tenir compte du sous-enregistrement, Afrique du sud.
Sexe masculin
| Sexe féminin
| |||||
|---|---|---|---|---|---|---|
| Age | Déclarés | Attendus | Rapport | Déclarés | Attendus | Rapport |
| 0-4 | ||||||
| 5-9 | 22 683 | 16 979 | 134% | 22 995 | 14 575 | 158% |
| 10-14 | 16 462 | 12 224 | 135% | 15 173 | 10 349 | 147% |
| 15-19 | 38 013 | 27 784 | 137% | 35 666 | 26 874 | 133% |
| 20-24 | 74 934 | 59 946 | 125% | 95 993 | 84 611 | 113% |
| 25-29 | 124 403 | 112 129 | 111% | 152 718 | 154 437 | 99% |
| 30-34 | 150 792 | 158 796 | 95% | 166 488 | 170 680 | 98% |
| 35-39 | 159 016 | 159 137 | 100% | 137 837 | 141 399 | 97% |
| 40-44 | 140 172 | 148 269 | 95% | 111 910 | 115 746 | 97% |
| 45-49 | 120 016 | 131 988 | 91% | 85 284 | 93 408 | 91% |
| 50-54 | 118 989 | 121 242 | 98% | 76 941 | 81 793 | 94% |
| 55-59 | 97 977 | 105 641 | 93% | 57 353 | 72 131 | 80% |
| 60-64 | 88 088 | 98 089 | 90% | 69 220 | 78 877 | 88% |
| 65-69 | 80 451 | 90 359 | 89% | 67 007 | 86 099 | 78% |
| 70-74 | 72 827 | 79 663 | 91% | 69 536 | 93 404 | 74% |
| 75-79 | 59 632 | 69 665 | 86% | 61 942 | 88 314 | 70% |
| 80-84 | 45 365 | 52 533 | 86% | 58 410 | 77 084 | 76% |
| 85+ | 51 779 | 50 387 | 103% | 83 753 | 108 002 | 78% |
Dans le cas où l’on ne dispose des décès des 12 derniers mois que dans le second recensement, on peut encore estimer les décès par âge dans l’intervalle intercensitaire, en partant seulement du second recensement, et en utilisant la formule suivante :
Dans le cas de l’Afrique du sud, en ne considérant que les données des décès des 12 derniers mois fournis par l’enquête de communauté de 2007, on trouve une estimation de la probabilité de décéder de 15 à 60 ans de 581 pour 1000 pour les hommes et de 556 pour 1000 pour les femmes. Certes, on a utilisé ici les données de la seconde enquête, à une date où la mortalité avait augmenté du fait de l’épidémie de VIH/sida par rapport à la période antérieure. Il est certain que calculer la mortalité à partir d’une seule année, qui plus est sur un échantillon de taille assez faible, produira vraisemblablement des estimations moins fiables, et dans ce cas surtout pour les femmes. D’autres études (Bradshaw, Dorrington et Laubscher 2012) suggèrent que la probabilité de décès pour l’année 2006 est plus proche de 550 pour 1000 pour les hommes, et de 450 pour 1000 pour les femmes.
Description détaillée de la méthode
Exposé mathématique
Le principe de base de la Méthode de l’extinction des cohortes synthétiques fut énoncé par Paul Vincent (1951): le nombre de personnes qui atteignent leur anniversaire à un instant donné doit être égal aux décès cumulés au-delà de cet âge dans la même cohorte, jusqu’au décès du dernier survivant. Cette méthode est simplement une généralisation de la méthode proposée par Preston, Coale, Trussell et al. (1980), qui, elle, exige que la population soit stable. Dans une cohorte suivie en longitudinal on a donc la relation suivante :
où représente le nombre de personnes de la cohorte qui atteignent l’âge a à l’instant t, et représente le nombre de décès au temps t + s, qui sont donc d’âge a + s, dans l’intervalle de temps infinitésimal ds.
En faisant l’hypothèse que les taux de mortalité sont constants au cours de l’intervalle, et en remarquant que le nombre de décès à un âge donné doit croitre à un taux égal au taux cumulé de croissance de la population du temps t à t + s, on peut calculer le nombre de décès dans l’intervalle selon la formule :
où< représente le taux de croissance annuel de la population d’âge a + s dans l’intervalle de temps de t + z à t + z + dz. Si la mortalité est constante dans le temps, on peut démontrer que et donc que:
Qui peut s’écrire comme:
(1)
On peut donc calculer la population attendue à chaque âge en connaissant les décès par âge qui se produisent sur un intervalle de temps et les taux de croissance par âge de la population. La comparaison de cette population attendue avec la population observée à un recensement peut fournir une estimation de la complétude de l’enregistrement des décès par rapport à celle de la population.
Mise en œuvre pratique de la méthode
Comme les données avec lesquelles on travaille sont en général sujettes à des erreurs sur l’âge, on travaille le plus souvent avec des groupes d’âge quinquennaux.
Considérons ici le cas où l’on dispose des données suivantes le nombre de décès déclarés sur un période de plusieurs années, entre les instants t1 et t2, répartis en groupe d’âge quinquennaux, notés , jusqu’à un intervalle d’âge ouvert commençant à l’âge A, noté ; et les effectifs de population aux mêmes instants t1 et t2, répartis selon les mêmes groupes d’âge (provenant de recensements exhaustifs), notés et (où t désigne soit t1 soit t2). On peut utiliser ces données directement pour appliquer la méthode : on calcule et , on prend comme approximation de la quantité : et pour la quantité :
Comme cela a été suggéré par Bennett et Horiuchi (1981), on peut calculer l’expression contenue dans l’équation 1 par récurrence, selon la formule suivante :
(2)
où représente le nombre de personnes qui atteignent l’âge x entre les deux recensements, c'est-à-dire entre t1 et t2, et où représente le taux de croissance annuels de la population qui atteint le groupe d’âge de x à x + 4 (âge au dernier anniversaire) entre les instants t1 et t2.
Bennett et Horiuchi (1981, 1984) proposent d’utiliser les taux de croissance par groupe d’âge pour améliorer à la fois aux âges élevés et , où A désigne l’âge au début du dernier intervalle d’âge, l’intervalle ouvert. Ils suggèrent de calculer comme suit:
où représente les décès déclaré à l’âge A et plus, et représente l’espérance de vie à l’âge A.
Pour tenir compte de la courbure aux âges élevés, ils suggèrent aussi de modifier l’équation 2 comme suit :
où :
De plus, ils suggèrent de faire une approximation au-delà de l’âge de 60 ans, imposant la courbe d’une population stable sur les intervalles de 5 ans, et d’estimer la quantité : en calculant l’aire située en dessous cette courbe (Bennett and Horiuchi 1981: 210). Mais en pratique, les données sont rarement suffisamment précises pour permettre un tel raffinement, et ce dernier ne ferait guère de différence sur l’estimation finale de la complétude.
En pratique, pour corriger, au moins en partie, les effets de la préférence pour les chiffres ronds dans les âges déclarés, et aussi pour rendre les données des décès compatibles avec celles de la population pour les groupes d’âge quinquennaux conventionnels, on calcule cette quantité de la manière suivante : . De plus, comme la séquence des rapports , et même la séquence des rapports comme le font remarquer Bennett et Horiuchi (1981), est en général assez erratique du fait des erreurs sur l’âge et des omissions différentielles des personnes dans certains groupes d’âge, il est courant de faire l’hypothèse que le sous-enregistrement est approximativement constant selon l’âge pour tous les âges supérieurs à un âge minimal, comme par exemple 10 ans. On calcule alors cette proportion fixe, c, en prenant soit la moyenne soit la médiane des rapports sur un intervalle d’âge donné (on peut aussi, si nécessaire, corriger arbitrairement les taux de croissance par âge, pour tenir compte de la différence de couverture des deux recensements). En fait, la différence de complétude des deux recensements est prise en compte en ajoutant une constante, , aux taux de croissance par âge calculés directement à partir des effectifs des populations recensées, delta étant choisi pour produire une séquence de même niveau des rapports : . Cette relation peut s’établir par les dérivations suivantes. Supposons que : et . Alors on a:
où:
Alors, , où t est la durée de l’intervalle intercensitaire, donne une indication de la différence de couverture des deux estimations de la population utilisées pour le calcul des taux de croissance par âge.
En général on donne une représentation graphique des rapports dans les groupes d’âge quinquennaux : , et des rapports dans les groupes d’âge cumulés :, définis comme
Cette dernière série tend à être plus stable, et facilite l’interprétation des données.
Extensions de la méthode
Si les âges sont précis, et si l’hypothèse de la couverture constante par âge des recensements est vérifiée (ce qui est peu probable), alors la méthode peut être adaptée aux cas où la complétude de la déclaration des décès n’est constante que sur un intervalle d’âges limité, (x to x+n). Dans ce cas on applique une version tronquée de la méthode, qui exclut des calculs les décès et la population d’âge supérieur ou égal à x+n. Cette adaptation peut s’appliquer aux données de l’état civil, par exemple, dans le cas où la complétude baisse au-delà de l’âge de la retraite, lorsque les personnes migrent des zones urbaines vers les zones rurales. Elle peut aussi s’appliquer aux décès déclarés par les ménages, lorsque ceux-ci sont sous-estimés car les ménages sont dissous suite au dernier décès d’adulte. Cependant, cette méthode a peu de chance d’être robuste, sauf peut-être quand l’âge x + n est élevé. Par contre, une adaptation analogue de la méthode généralisée de la balance de l’accroissement démographique est plus simple, et semble un peu plus robuste.
Autres lectures et références
L’analyse de la sensibilité de cette méthode aux erreurs de données les plus fréquentes et aux violations des hypothèses sous-jacentes reste assez limitée. Toutefois, on renvoie le lecteur aux documents suivants : à Hill, You et Choi (2009) pour ce qui concerne les hypothèses de la méthode de la répartition des décès dans les populations sans VIH/sida; et à Dorrington et Timæus (2008) pour le cas des populations souffrant d’une forte épidémie de VIH/sida. Par contre, Murray, Rajaratnam, Marcus et al. (2010) présentent une analyse de sensibilité utilisant des méthodes stochastiques. Ils concluent que ces méthodes ne sont pas vraiment fiables, mais peut-être cette conclusion est-elle due à des hypothèses irréalistes sur les migrations.
Bennett NG and S Horiuchi. 1981. "Estimating the completeness of death registration in a closed population", Population Index 47(2):207-221. doi: https://dx.doi.org/10.2307/2736447
Bennett NG and S Horiuchi. 1984. "Mortality estimation from registered deaths in less developed countries", Demography 21(2):217-233. doi: https://dx.doi.org/10.2307/2061041
Blacker J. 1988. An Evaluation of the Pakistan Demographic Survey. Karachi: Pakistan Federal Bureau of Statistics. https://dx.doi.org/10.2307/2061041
Bradshaw D, RE Dorrington and R Laubscher. 2012. Rapid Mortality Surveillance Report 2011. Cape Town: South African Medical Research Council. https://www.samrc.ac.za/sites/default/files/attachments/2022-08/RapidMortality2011.pdf
Dorrington RE, TA Moultrie and IM Timæus. 2004. Estimation of mortality using the South African 2001 census data. Monograph 11. Centre for Actuarial Research, University of Cape Town. https://blogs.lshtm.ac.uk/iantimaeus/files/2024/03/Dorrington-Moultrie-Timaeus-Mono11.pdf
Dorrington RE and IM Timæus. 2008. "Death Distribution Methods for Estimating Adult Mortality: Sensitivity Analysis with Simulated Data Errors, Revisited," Paper presented at Population Association of America 2008 Annual Meeting. New Orleans, Louisiana, 17-19 April.
Hill K, D You and Y Choi. 2009. "Death distribution methods for estimating adult mortality: Sensitivity analysis with simulated data error", Demographic Research 21(Article 9):235-254. doi: https://dx.doi.org/10.4054/DemRes.2009.21.9
Murray CJL, JK Rajaratnam, J Marcus, T Laakso and AD Lopez. 2010. "What can we conclude from death registration? Improved methods for evaluating completeness", PLoS Med 7(4):e1000262. doi: https://dx.doi.org/10.1371/journal.pmed.1000262
Preston SH, AJ Coale, J Trussell and M Weinstein. 1980. "Estimating the completeness of reporting of adult deaths in populations that are approximately stable", Population Index 46:179-202. doi: https://dx.doi.org/10.2307/2736122
Timæus IM. 2007. "Impact of HIV on mortality in Southern Africa: Evidence from demographic surveillance", in Caraël M and JR Glynn (eds). HIV, Resurgent Infections and Population Change in Africa, Springer, pp 229–243. doi: https://dx.doi.org/10.1007/978-1-4020-6174-5_12
UN Population Division. 2011. World Population Prospects: The 2010 Revision, Volume I: Comprehensive Tables. New York: United Nations, Department of Economic and Social Affairs, ST/ESA/SER.A/313. https://www.un.org/development/desa/pd/sites/www.un.org.development.desa.pd/files/files/documents/2020/Jan/un_2010_world_population_prospects-2010_revision_volume-i_comprehensive-tables.pdf
Vincent P. 1951. "La mortalite des vieillards", Population 6:182-204. doi: https://dx.doi.org/10.2307/1524149
- Printer-friendly version
- Log in to post comments
