Estimation indirecte de la mortalité adulte à partir des proportions d’orphelins

Description de la méthode

La méthode des proportions d’orphelins consiste à estimer la mortalité des hommes et femmes adultes à partir des données sur la survie des père et mère des répondants. Pour que la méthode puisse être appliquée, il est nécessaire qu’au moins un recensement ou une enquête auprès de la population ait inclus les questions ‘Votre mère est-elle en vie ?’ et ‘Votre père est-il en vie ?’. La mortalité peut être estimée sans qu’il soit nécessaire de demander aux répondants de se rappeler les dates de décès ou les âges au décès des individus décédés.

Comme les mères doivent avoir été vivantes au moment où les répondants sont nés, la durée où elles ont été exposées au risque de décéder est égale à l’âge des répondants. En prenant en compte l’âge moyen auquel les mères ont leurs enfants dans la population concernée, on peut prévoir la probabilité de survie de la table de mortalité de 25 ans à 25 ans plus un nombre arrondi d’années (n) en fonction du groupe d’âge des répondants (l_25+n/l₂₅), en s’appuyant sur la proportion des répondants de chaque groupe d’âge dont la mère est en vie. De même, en considérant l’âge moyen auquel les pères ont leurs enfants, on peut prévoir la probabilité de survie des hommes adultes dans la table de mortalité à partir des proportions de répondants dont les pères sont encore en vie. Comme les hommes tendent à être plus âgés que leurs épouses et autres partenaires, leur survie est mesurée entre 35 ans et 35 + n ans, où n dépend à nouveau du groupe d’âge des répondants.

Si la mortalité a évolué au fil du temps, les rapports de survie estimés reflètent des taux de mortalité qui ont prévalu à divers âges et diverses périodes. Une méthode de ‘localisation dans le temps’ a été développée pour estimer combien d’années avant le recensement chaque proportion de survivants dans les cohortes égale la proportion de survivants par période. Ces intervalles s’accroissent avec l’âge des répondants, s’étageant entre 4 et 14 ans avant la collecte des données. Ainsi, si les rapports de survie estimées à partir des déclarations des répondants des différents groupes d’âge sont traduits en indice courant de la mortalité des adultes (par exemple ₄₅q₁₅) grâce à un système de tables types de mortalité à 1 paramètre, ces statistiques se rapporteront à diverses dates et pourront être utilisées pour retracer l’évolution de la mortalité dans le temps.

Les méthodes des proportions d’orphelins ont un avantage sur les questions concernant les décès survenus dans le ménage, qui nécessitent des recensements ou des enquêtes exceptionnellement larges pour recueillir des informations sur un nombre suffisant de décès dans les ménages dans l’année précédant l’enquête, afin que les estimations de la mortalité soient assez précises pour être utiles. La méthode des proportions d’orphelins peut être utilisée dans des enquêtes beaucoup plus petites, même si toutes les méthodes d’estimation de la mortalité adulte nécessitent des données sur des milliers de ménages. En outre, la méthode ne nécessite pas que la population soit fermée à la migration. Les résultats ne seront toutefois pas représentatifs concernant des petits états ou des régions dans lesquels une proportion substantielle de la population aura émigré ou sera composée d’immigrés.

Données nécessaires et hypothèses

Tableaux de données nécessaires

Pour estimer la mortalité des femmes adultes :

• La proportion de répondants dont la mère est vivante par groupe quinquennal d’âge du répondant. (Ceux qui ne savent pas si leur mère est vivante ou qui n’ont pas répondu à la question doivent être exclus des calculs.)
• Le nombre de naissances dans l’année précédant le recensement ou l’enquête classé par groupe quinquennal d’âge de la mère.

Pour estimer la mortalité des hommes adultes :

• La proportion de répondants dont le père est vivant par groupe quinquennal d’âge du répondant. (Ceux qui ne savent pas si leur père est vivant ou qui n’ont pas répondu à la question doivent être exclus des calculs.)
• Le nombre de naissances dans l’année précédant le recensement ou l’enquête classé par groupe quinquennal d’âge de la mère.
• Une estimation de la différence d’âge entre les hommes et les femmes ayant des enfants, par exemple la différence entre les âges médians des hommes et des femmes actuellement mariés.

Ces tableaux doivent généralement être établis séparément pour les répondants hommes et femmes et les estimations sont faites à partir des deux séries de proportions et pour les deux sexes ensemble.

Pour estimer la mortalité, le mieux est que les questions sur la survie des père et mère soient posées à toutes les personnes de moins de 50 ans (le plus simple peut être de poser les questions à tout le monde). Si toutefois elles n’ont concerné que les enfants orphelins, les données peuvent être utilisées pour une estimation ponctuelle de la mortalité des hommes et des femmes quelques années plus tôt.

Si des pondérations d’échantillonnage vous ont été fournies en même temps que les données, n’oubliez pas de les incorporer de manière appropriée dans votre logiciel quand vous établirez les tableaux de base.

Hypothèses importantes

Une limitation inhérente à la méthode des proportions d’orphelins est que les données relatives à la survie des parents ne peuvent être recueillies qu’auprès de ceux de leurs enfants eux-mêmes survivants. La survie des adultes sans enfants vivants n’est pas représentée dans les déclarations concernant la survie des parents. En outre, les parents ayant plus d’un enfant survivant sont surreprésentés par rapport à ceux n’en ayant qu’un, en proportion du nombre de leurs enfants survivants. La méthode ne produit donc des résultats non biaisés que si la mortalité des parents n’est pas reliée au nombre de leurs enfants vivants au moment où les données sont recueillies. En général, le biais de sélection dû au non respect des cette hypothèse est modeste (Palloni, Massagli and Marcotte 1984). Dans des populations touchées par une épidémie généralisée de Sida, il peut cependant être plus sévère. Les méthodes qui traitent au moins en partie les biais spécifiques à ce type de population sont présentées dans une section particulière de ce chapitre sur les orphelins dans les populations touchées par le Sida.

La méthode des proportions d’orphelins permet d’estimer l’évolution de la mortalité à partir des données fournies par les répondants de différents groupes d’âge : plus les répondants sont âgés, plus est ancien en moyenne le décès de leurs parents. Pour convertir les séries de mesures de la survie obtenues à partir de différents groupes d’âge en un indicateur unique qui puisse être comparé au fil du temps, on doit supposer que le schéma de mortalité aux âges adultes est correctement représenté par la table de mortalité standard choisie. Pour estimer la localisation dans le temps de ces mesures, il faut en outre supposer que la mortalité a reculé linéairement en termes de ce standard au long de la période considérée. Ces deux hypothèses risquent de poser problème dans des populations touchées par une épidémie généralisée de Sida.

Travaux préparatoires et recherches préliminaires

Avant de débuter l’analyse, il convient de vérifier combien de répondants ont déclaré ne pas savoir si leur mère ou, plus fréquemment, leur père était vivant ou n’ont pas répondu du tout aux questions. Le taux de réponse à ces questions est généralement très élevé et on peut se contenter d’exclure de l’analyse ceux qui ont répondu ‘ne sait pas’ ou qui n’ont pas répondu à la question. En effet, ceci revient à supposer que la proportion des parents de ces répondants qui sont décédés est la même que pour ceux qui ont répondu à la question. Toutefois, quelques enquêtes ont recueilli des données suffisamment incomplètes pour suggérer que le biais de non-réponse pourrait être un problème important. Il se peut par exemple que la plupart des personnes qui ne répondent pas à la question aient des parents décédés. Si c’est le cas, ces orphelins non déclarés comme tels peuvent représenter une proportion importante de l’ensemble des orphelins, en particulier aux jeunes âges et les estimations finales de la mortalité peuvent se trouver fortement biaisées vers le bas.

Un contrôle utile sur la qualité des données concernant les orphelins peut consister à comparer les réponses des hommes et des femmes du même âge. On ne s’attend pas à ce que la proportion de parents décédés diffère significativement entre les hommes et les femmes du même âge. Si les proportions divergent parmi les répondants âgés, ce peut être dû à des différences entre hommes et femmes dans les erreurs de déclaration des âges ou cela peut indiquer que le genre qui déclare moins de décès de parents (en général les hommes) a sans doute davantage perdu contact avec la famille et suppose à tort que certain parent est encore vivant.

Précautions et mises en garde

• Les estimations obtenues par la méthode des proportions d’orphelins sont des probabilités conditionnelles de survie, c'est-à-dire des probabilités de survivre au cours d’un intervalle de l’âge adulte conditionnées par le fait d’être en vie au début de l’intervalle. Pour avoir une table de mortalité complète, il faut insérer des estimations de la survie depuis la naissance jusqu’à l’âge adulte tirées d’une autre source de données sur la mortalité des jeunes enfants.
• Les décès des parents ne surviennent pas en un point du temps mais peuvent être survenus à n’importe quel moment entre la naissance des répondants et la date de leur interview. La méthode des proportions d’orphelin ne peut indiquer qu’une évolution lissée de la mortalité ; elle est incapable de saisir des crises de mortalité de court terme ou des renversements abrupts de tendance comme ceux résultant du Sida après l’apparition d’une épidémie généralisée.
• Les données sur les proportions d’orphelins à la base des estimations de mortalité les plus récentes sont celles relatives aux enfants de 5-14 ans. En général, ceux-ci sont seulement quelques pour cents à être orphelins de mère et les estimations qui en résultent peuvent avoir de larges intervalles de confiance, même quand les enquêtes sont faites auprès de larges échantillons.
• Dans diverses applications en Afrique de l’est et ailleurs, la méthode des proportions d’orphelins a donné des résultats qui indiquent des baisses rapides de mortalité peu vraisemblables et de fortes incohérences entre les estimations tirées d’enquêtes successives. Ceci apparaît dû à ‘l’effet d’adoption’, c'est-à-dire une sous-déclaration de la perte des parents lorsque celle-ci est survenue alors que les enfants étaient très jeunes (Blacker 1984; Blacker and Gapere 1988; Hill 1984; Timæus 1986). Dans ces cas, les enfants sont souvent élevés par d’autres parents, dont ils apparaissent fréquemment comme les propres enfants dans les données de recensement. Ils sont alors considérés comme ayant un père ou une mère vivant, ce qui peut se traduire par des estimations très basses de la mortalité. Cette erreur apparaît particulièrement fréquente en cas de décès de la mère. A mesure que les répondants avancent en âge, la probabilité s’accroit que, en plus du parent biologique, le parent d’accueil, le parent adoptif ou le beau-parent soit également décédé. Il en résulte que le biais est surtout fort pour les jeunes enfants, car le parent substitut a de fortes chances d’être vivant. S’il n’est pas reconnu, l’effet d’adoptions conduit à une sous-estimation de la mortalité adulte récente et à une surestimation de l’ampleur de la baisse de la mortalité.
• Des estimations peuvent être faites à partir des données de répondants d’une quarantaine d’années, dont les parents sont souvent âgés et ont une mortalité très élevée. La précision avec laquelle on peut estimer à la fois la mortalité à partir des données sur la survie des parents et les dates de référence des estimations est donc beaucoup moindre que pour les répondants jeunes.
• La méthode des proportions d’orphelins n’inclut pas d’hypothèse sur l’absence de migration. Il peut néanmoins être difficile d’interpréter des estimations de la mortalité adulte tirées des proportions d’orphelins pour des unités géographiques infranationales, comme des fractions urbaines et rurales, ou pour des répondants ayant des caractéristiques socioéconomiques spécifiques. Certains des parents de répondants vivront ailleurs que les répondants eux-mêmes et leurs caractéristiques socioéconomiques diffèreront de celles de leurs enfants. Mais parents et enfants partagent généralement la même identité ethnique.

Application de la méthode

Les orphelins de mère

Etape 1a : Calculer $${\overline{M}}^f$$, l’âge moyen des femmes à la naissance de leurs enfants

Pour appliquer la méthode des proportions d’orphelins, on doit disposer d’une estimation de l’âge moyen auquel les parents ont eu leurs enfants afin de prendre en compte la variation dans l’éventail des âges où ils ont été exposés au risque de décéder. L’âge moyen des femmes à la naissance de leurs enfants est généralement calculé à partir des données de recensement ou d’enquête sur les naissances récentes par groupe quinquennal d’âge à l’interview des femmes ayant eu un enfant. La mesure est simplement l’âge moyen des femmes ayant eu une naissance, sans ajustement prenant en compte la structure par âge de la population, selon la formule suivante :

$${\overline{M}}^f=\frac{{\displaystyle \sum _{x=15}^{45}{}_{5}B{}_x\left(x+2\right)}}{{\displaystyle \sum _{x=15}^{45}{}_{5}B{}_x}}$$

Dans cette équation, ₅B_x représente les naissances des femmes du groupe d’âge entre x et x + 4 ans révolus et (x + 2) représente le point médian du groupe d’âge décalé vers le bas d’une demi année, pour tenir compte du fait que les femmes ayant une naissance au cours de l’année précédant l’interview l’ont eu en moyenne 6 mois plus tôt et qu’elles étaient donc alors 6 mois plus jeunes. Ce calcul peut être réalisé dans le fichier Excel joint. Si les données utilisées pour calculer $${\overline{M}}^f$$ sont classées par âge des femmes au moment de l’accouchement, le point médian de chaque groupe d’âge est égal à x + 2,5.

Il n’est pas nécessaire d’ajuster les données relatives aux naissances pour corriger les erreurs sur la période de référence avant de calculer $${\overline{M}}^f$$. En outre, les estimations de mortalité sont peu sensibles aux biais dans cet indicateur. Toutefois, s’il apparaît que la répartition par âge des naissances a été sévèrement déformée, parce que les femmes ont exagéré leur âge, le nombre de naissances par âge peut être recalculé à partir d’une distribution des âges et d’une distribution de la fécondité ajustées avant le calcul de $${\overline{M}}^f$$.

En principe, l’âge moyen à la maternité doit se référer au moment où les répondants sont nés, ce qui peut se situer entre 5 et 45 ans avant le recueil des données sur la survie des parents. Une estimation s’appuyant sur les données de fécondité recueillies dans l’enquête même où sont collectées les informations sur les orphelins peut convenir dans des populations qui n’ont pas encore connu de baisse importante de la fécondité. Si on pense que la fécondité a reculé et qu’il existe des données de recensement ou d’enquête antérieures, $${\overline{M}}^f$$ peut aussi être calculé à partir de ces données pour voir s’il a évolué. Si c’est le cas, la meilleure façon de décider des valeurs finales de $${\overline{M}}^f$$ pour l’estimation de la mortalité adulte dépendra des données disponibles et du schéma d’évolution de la fécondité. Une option peut être de calculer $${\overline{M}}^f$$ à partir de données recueillies environ au moment où la fécondité a commencé à baisser, d’utiliser cette valeur pour les groupes d’âge des répondants nés à cette époque ou antérieurement, et d’interpoler linéairement entre cette valeur et la valeur actuelle pour estimer pour des femmes plus jeunes.

Etape 2a : Calculer les rapports conditionnels de survie des tables de mortalité pour les femmes

Le fichier Excel joint contient des feuilles séparées pour le calcul des rapports de survie des femmes adultes (Orphelins de mère) et des hommes adultes (Orphelins de père). Les feuilles sont établies à la fois pour analyser les données des répondants masculins et féminins séparément et pour les combiner afin de produire des estimations fondées sur les données fournies simultanément par les deux sexes. Sur la feuille des orphelins de mère, il faut entrer soit le nombre de répondants de chaque sexe par groupe quinquennal d’âge dont la mère survit et le nombre de ceux qui ont répondu à la question, soit les proportions de ceux dont la mère survit calculées à partir de ces nombres.

La survie des femmes est estimée entre une limite inférieure de 25 ans et 25 + n ans, où n est la limite supérieure de chacun des groupes d’âge successifs des répondants. Nous utilisons l’équation de régression suivante et les coefficients figurant au tableau 1 :

$${}_{n}p{}_{25}=a(n)+b(n){\overline{M}}^f+c(n){}_{5}S{}_{n-5}$$

où ₅S_n-5 est la proportion de répondants dans le groupe d’âge entre les anniversaires n – 5 et n ayant leur mère vivante. Par exemple, quand n est égal à 10, la survie dans les tables de mortalité est estimée sur un intervalle de 10 ans entre les 25^ème et 35^ème anniversaires, à partir des données sur la survie des mères fournies par les répondants de 5-9 ans.

Tableau 1 Coefficients pour l’estimation de la survie des femmes à partir des proportions de répondants dont la mère est vivante 

n	a(n)	b(n)	c(n)
10	-0,2894	0,00125	1,2559
15	-0,1718	0,00222	1,1123
20	-0,1513	0,00372	1,0525
25	-0,1808	0,00586	1,0267
30	-0,2511	0,00885	1,0219
35	-0,3644	0,01287	1,0380
40	-0,5181	0,01795	1,0753
45	-0,6880	0,02343	1,1276
50	-0,8054	0,02721	1,1678
Source: Timæus (1992)

 

Orphelins de père

Etape 1b : Calculer $${\overline{M}}^m$$, l’âge moyen des hommes à la naissance de leurs enfants

En principe, la meilleure façon de calculer l’âge moyen auquel les hommes ont des enfants consiste à calculer l’âge moyen des partenaires des femmes qui ont eu une naissance une année donnée. Mais la méthode nécessite qu’existe un lien entre les données des femmes et celles de leur partenaire, ce qui n’est pas le cas la plupart du temps.

L’âge moyen auquel les hommes ont leurs enfants est donc généralement estimé en ajoutant à l’âge moyen des femmes à la maternité une mesure de la différence d’âge entre les hommes et les femmes ayant des enfants :

$${\overline{M}}^m={\overline{M}}^f+d$$.

Une estimation de cette différence qui peut être calculée aisément à partir des données de recensement est la différence entre les âges médians des hommes et des femmes actuellement mariés. C’est une solution plus appropriée que la différence entre les âges moyens au premier mariage des hommes et des femmes, dans les populations où les dissolutions d’union et les mariages polygames sont courants. La médiane est préférée à la moyenne de sorte que la surestimation différentielle des âges par les répondants âgés, dont la fécondité est vraisemblablement nulle de toute façon, n’affecte pas l’estimation.

Cette procédure d’estimation de l’âge moyen des hommes à la naissance de leurs enfants revient à supposer que les âges des pères des enfants nés de mères non mariées sont égaux, en moyenne, aux âges des pères des enfants nés de mères mariées. Ce n’est pas nécessairement le cas et cela peut introduire un biais significatif dans l’estimation de $${\overline{M}}^m$$ dans les populations où la fécondité hors mariage est importante. Ce problème est difficile à résoudre mais, heureusement, les estimations de la mortalité sont peu sensibles aux erreurs dans la mesure de $${\overline{M}}^m$$.

Etape 2b : Calculer les rapports conditionnels de survie des tables de mortalité pour les hommes

Le fichier Excel joint contient des feuilles séparées pour le calcul des rapports de survie pour les femmes adultes et les hommes adultes. Sur la feuille des orphelins de père, il faut entrer soit le nombre de répondants de chaque sexe par groupe quinquennal d’âge dont le père survit et le nombre de ceux qui ont répondu à la question, soit les proportions de ceux dont le père survit calculées à partir de ces nombres. Les données ne sont utilisées que pour les répondants âgés de 5 à 44 ans.

Chaque estimation de la survie des hommes est obtenue à partir des données de deux groupes quinquennaux d’âge adjacents. Pour chaque paire de groupes d’âge, sauf la paire la plus jeune analysée, la survie des hommes est mesurée de 35 ans à 35 + n, où n est le point médian de la paire de groupes d’âge, en utilisant l’équation de régression suivante et les coefficients figurant au tableau 2 :

$${}_{n}p{}_{35}=a(n)+b(n){\overline{M}}^m+c(n){}_{5}S{}_{n-5}+d(n){}_{5}S{}_n$$

Par exemple, quand n est égal à 10, la survie de la table de mortalité est estimée sur un intervalle de 10 ans du 35^ème au 45^ème anniversaire, à partir des données sur la survie des pères fournies par les répondants des deux groupes d’âge 5-9 et 10-14 ans.

Pour la paire de groupes d’âge la plus jeune, ce rapport de survie est nettement supérieur aux proportions de pères vivants, ce qui rend les estimations très sensibles au schéma exact de mortalité par âge dans la population. Des estimations plus robustes sont obtenues grâce à l’équation :

$${}_{15}p{}_{35}=a(10)+b(10){\overline{M}}^m+c(10){}_{5}S{}_5+d(n){}_{5}S{}_{10}$$

En d’autres termes, le même rapport de survie, ₁₅q₃₅, est estimé à partir des données des répondants âgés à la fois de 5-14 et de 10-19 ans.

Tableau 2 Coefficients pour l’estimation de la survie des hommes à partir des proportions de répondants dont le père est vivant

n	a(n)	b(n)	c(n)	d(n)
10	-0,5578	0,00040	1,4708	0,0698
15	-0,4013	0,00576	1,5602	-0,3522
20	-0,3329	0,01031	0,6656	0,3419
25	-0,4726	0,01559	0,2161	0,7896
30	-0,7056	0,02076	0,1997	0,9066
35	-0,9153	0,02493	0,3484	0,8631
40	-0,9950	0,02635	0,4269	0,8263
Source: Timæus (1992)

 

Orphelins de mère et de père

Etape 3 : Convertir les rapports de survie en estimations du niveau de mortalité

Pour établir une évolution de la mortalité à partir d’une série de rapports de survie, _np_b, obtenus à partir de différents groupes d’âge de répondants et se rapportant à différentes dates, il convient de les convertir en un indice commun de mortalité qui puisse être comparé dans le temps. Nous le faisons en ajustant une table-type de mortalité à 1 paramètre à chaque mesure et en obtenant l’indice commun de mortalité de la table-type.

Des indices très variés ont ainsi été utilisés, incluant les paramètres de niveau de divers systèmes de tables-types de mortalité, des rapports de survie comme ₃₅p₃₀, qui correspondent bien à l’intervalle d’âge couvert par la méthode des proportions d’orphelins, l’espérance de vie à divers âges entre 5 et 30 ans et l’espérance de vie temporaire entre 25 et 70 ans, ₄₅e₂₅. L’utilisation des paramètres des tables-types a l’avantage de souligner que la table de mortalité complète est estimée par l’ajustement d’un modèle, plutôt que d’être mesurée directement. Les mesures de l’espérance de vie résument la survie sur l’ensemble des âges adultes, alors que l’utilisation des rapports de survie ou des espérances de vie temporaires évite l’extrapolation aux âges avancés à partir de mesures faites à des âges plus jeunes. Récemment, les estimations ont été présentées de plus en plus souvent en termes de probabilité de décéder entre le 15^ème et le 60^ème anniversaire, ₄₅q₁₅, car cette mesure a la faveur de plusieurs agences internationales comme indicateur résumé de la mortalité des adultes jeunes et d’âge moyen.

Dans les applications de la méthode des proportions d’orphelins présentées ici, les rapports de survie sont convertis en paramètre α d’un système à 1 paramètre de tables-types de mortalité logit relationnelles puis en estimations de la probabilité de décéder entre le 15^ème et le 60^ème anniversaire, ₄₅q₁₅, ou en probabilité de décéder entre le 30^ème et le 60^ème anniversaire, ₃₀q₃₀. Cette dernière mesure est utile quand il s’agit de comparer entre elles des séries d’estimations tirées des proportions d’orphelins sans extrapoler de la mortalité sur un intervalle d’âge à la mortalité sur un autre intervalle davantage qu’il n’est nécessaire. Les paramètres des modèles à 1 paramètre sont calculés à partir des estimations de _np_b :

$$\alpha =-\frac{1}{2}\ln \left(1+\frac{\frac{{}_{n}p{}_b}{l_{b+n}^s}-\frac{1}{l_b^s}}{1-{}_{n}p{}_b}\right)$$

où les estimations de _np_b proviennent de l’étape 2, avec b = 25 pour les estimations de la survie des femmes et b = 35 pour celles de la survie des hommes, et où les valeurs de $$l_x^s$$ proviennent de la table de mortalité standard. On obtient donc une série de valeurs de α correspondant aux mesures de la survie conditionnelle prises à partir des données de différents groupes d’âge de répondants. Des valeurs élevées de α correspondent à une mortalité forte. Et pour chaque α :

$${}_{45}q{}_{15}=1-\frac{1+e^{2\left(\alpha +Y_s(15)\right)}}{1+e^{2\left(\alpha +Y_s(60)\right)}}$$

ou

$${}_{30}q{}_{30}=1-\frac{1+e^{2\left(\alpha +Y_s(30)\right)}}{1+e^{2\left(\alpha +Y_s(60)\right)}}$$

Le fichier Excel joint permet de calculer α, ₄₅q₁₅ et ₃₀q₃₀ en utilisant un standard tiré soit du réseau Général des tables-types de Nations Unies, soit d’un des quatre réseaux des tables-types de Princeton. La table standard doit être choisie parce qu’elle a un schéma de mortalité par âge aux âges adultes qui ressemble à celui de la population étudiée. Une autre table peut être utilisée comme standard, s’il y a des raisons de penser qu’elle ressemble davantage au schéma de mortalité adulte de la population étudiée. La table de mortalité la mieux adaptée n’appartient pas nécessairement au réseau de tables-types qui reproduit le mieux la relation entre la mortalité aux jeunes âges et à l’âge adulte. Si on ne sait rien du schéma par âge de la mortalité des adultes, il est recommandé d’utiliser le réseau Général des Nations Unies ou le réseau Ouest de Princeton.

Etape 4 : Calculer la localisation dans le temps des estimations

Chaque rapport de survie obtenu par la méthode des proportions d’orphelins représente une moyenne de la mortalité ayant eu cours pendant les N années où les parents ont été exposés au risque de décéder. Le point du temps où le rapport est égal à la survie du moment dépend du niveau de la mortalité et peut être estimé à partir de la proportion de pères ou de mères en vie, de l’âge des répondants et de l’âge moyen des parents à la naissance des enfants.

La seule information supplémentaire nécessaire pour calculer les dates auxquelles s’applique chacune des estimations de la mortalité adulte est la date où les répondants ont été interrogés sur la survie de leurs père et mère. Cette information peut être calculée comme la moyenne des dates où les interviews ont eu lieu ou peut être prise comme le point médian de la période de travail sur le terrain si les dates précises des interviews ne sont pas disponibles.

Les estimations sont égales à la date du travail de terrain moins T, où T est calculé comme suit pour les femmes :

$$T=\frac{N}{2}\left(1-\frac{1}{3}\ln \left({}_{5}S{}_{n-5}\right)+\frac{1}{3}\ln \left(\frac{80-{\overline{M}}^f-N}{80-{\overline{M}}^f}\right)\right)$$

Comme la mortalité des mères est estimée à partir des données des répondants d’un seul groupe quinquennal d’âge, leur durée moyenne d’exposition au risque de décéder, N, est le point médian de ce groupe d’âge (c'est-à-dire 7,5 ans, 12,5 ans, etc.). Mais comme des paires de groupes d’âge sont utilisées pour estimer la mortalité des hommes, N est cette fois l’âge qui sépare les deux groupes d’âge (c'est-à-dire 10 ans, 15 ans, etc.). Comme en outre les pères peuvent être décédés pendant les 9 mois avant que les répondants soient nés, T devient 

$$T=\frac{(N+0,75)}{2}\left(1-\frac{1}{3}\ln (\sqrt{{}_5{}^{}S{}_{n-5}\cdot {}_5{}^{}S{}_n})+\frac{1}{3}\ln \left(\frac{80-{\overline{M}}^m-N}{80-({\overline{M}}^m-0,75)}\right)\right).$$

Pour la mortalité des hommes aussi bien que des femmes, la localisation dans le temps des estimations obtenues à partir des proportions d’orphelins parmi les répondants des différents groupes d’âge au-delà de 30 ans est généralement la même. La date à laquelle peuvent avoir lieu les premiers décès de parents devient plus précoce à mesure qu’augmente l’âge des répondants, mais ceci est contrebalancé par l’accroissement de la proportion de décès survenus peu avant l’enquête à mesure que les parents sont plus âgés. Il arrive que la localisation dans le temps des indicateurs de mortalité tirés des données des groupes d’âge les plus avancés soit plus récente que la localisation des indicateurs tirés des données de répondants cinq ans plus jeunes. Etant donné la nature approximative de l’équivalence posée entre mesures de mortalité des cohortes et estimations du moment, il est souvent recommandé d’omettre les estimations tirées des groupes d’âge les plus avancés ou de faire la moyenne des deux ou trois estimations finales et des dates auxquelles elles se référent pour n’en tirer qu’une seule mesure.

Exemple

Nous utilisons les données sur la survie des mères et des pères recueillies lors du recensement de 1997 en Irak disponibles grâce à IPUMS. Nous ne présentons les résultats que pour les deux sexes réunis.

Etape 1a : Calculer $${\overline{M}}^f$$ , l’âge moyen des femmes à la naissance de leurs enfants

L’âge moyen à la naissance des enfants est une moyenne simple des âges des femmes à l’accouchement. Il peut être calculé à partir des données individuelles ou estimé approximativement à partir d’un tableau des naissances par groupe quinquennal d’âge des mères (tableau 3).

$${\overline{M}}^f=\frac{173338360}{613080}=28,28$$

 

Tableau 3 Calcul de l’âge moyen à la naissance des enfants, Irak, 1997

Groupe d’âge	Naissances de la dernière année B(i)	Age au point médian N	B(i)*N
15-19	50 720	17	862 240
20-24	147 040	22	3 234 880
25-29	174 350	27	4 707 450
30-34	129 860	32	4 155 520
35-39	66 440	37	2 458 280
40-44	35 900	42	1 507 800
45-49	8 770	47	412 190
Totaux:	613 080		17 338 360

 

Etape 2a : Calculer les rapports conditionnels de survie des tables de mortalité pour les femmes

Les rapports de survie sont dans la sixième colonne du tableau 4 ; ils sont calculés à partir des proportions de la quatrième colonne, en utilisant les coefficients de régression du tableau 1 et l’estimation de $${\overline{M}}^f$$, égale à 28,28 ans à l’étape 1a. Par exemple, pour les répondants âgés de 5-9 ans :

$${}_{10}{}^{}p{}_{25}=-0,2894+0,00125\times 28,28+1,2559\times 0,9916=0,9913.$$

Notez que les mesures de la table de mortalité sont du même ordre que les proportions à partir desquelles elles ont été calculées.

Tableau 4 Estimation de la survie des femmes, des dates auxquelles ces estimations sont localisées dans le temps, et estimations correspondantes de α et ₃₀q₃₀ tirées des proportions d’orphelins de mère, Irak, Recensement de 1997, Sexes réunis  

Groupe d’âge	Total des femmes	Mère vivante	Proportion mère vivante	Age n	l (25+n) l (25)	Niveau (α)	Probabilité de décéder  (30q30)	Date
5 - 9	2 834 210	2 810 420	0,9916	10	0,9913	-0,756	0,072	1994,2
10-14	2 391 580	2 347 190	0,9814	15	0,9826	-0,670	0,084	1992,1
15-19	2 181 840	2 108 280	0,9663	20	0,9709	-0,625	0,090	1990,1
20-24	1 827 030	1 719 880	0,9414	25	0,9514	-0,561	0,101	1988,5
25-29	1 615 160	1 455 150	0,9009	30	0,9198	-0,497	0,112	1987,0
30-34	1 235 120	1 035 480	0,8384	35	0,8698	-0,438	0,124	1985,9
35-39	788 170	601 590	0,7633	40	0,8103	-0,447	0,122	1985,4
40-44	817 460	519 580	0,6356	45	0,6910	-0,375	0,137	1985,5
45-49	603 840	298 760	0,4948	50	0,5419	-0,346	0,144	1988,3

 

Etape 1b : Calculer $${\overline{M}}^m$$, l’âge moyen des hommes à la naissance de leurs enfants

 

L’âge moyen des hommes à la naissance de leurs enfants est obtenu en ajoutant la différence entre les âges médians des hommes et des femmes actuellement mariés à l’âge moyen des femmes à la naissance de leurs enfants. On voit au tableau 5 que l’âge médian des hommes actuellement mariés est compris entre le point médian du groupe 30-34 ans et le point médian du groupe 35-39 ans. Par interpolation linéaire,

$$\text{Age}\text{médian des hommes}=32,5+5\times \frac{0,5-0,4105}{0,5208-0,4105}=36,56$$

et

$$\text{Age médian des femmes}=27,5+5\times \frac{0,5-0,3780}{0,5372-0,3780}=31,33$$

 

Tableau 5 Ages des hommes et des femmes actuellement mariés, Irak, 1997

Groupe d’âge	Hommes mariés	Femmes mariées	Proportion cumulée d’hommes	Proportion cumulée de femmes
10-14	1 380	7 300	0,0005	0,0024
15-19	34 140	171 320	0,0122	0,0583
20-24	192 160	429 420	0,0782	0,1984
25-29	471 780	550 700	0,2401	0,3780
30-34	496 440	488 090	0,4105	0,5372
35-39	321 400	345 680	0,5208	0,6500
40-44	375 650	336 270	0,6497	0,7597
45-49	279 350	245 010	0,7456	0,8396
50-54	224 610	164 470	0,8227	0,8933
55-59	166 800	115 380	0,8800	0,9309
60-64	105 760	75 470	0,9163	0,9555
65-69	99 360	63 890	0,9504	0,9764
70-74	59 000	37 220	0,9706	0,9885
75-79	41 110	19 700	0,9847	0,9949
80+	44 430	15 570	1,0000	1,0000
Total	2 913 370	3 065 490

 

L’âge moyen des hommes à la naissance de leurs enfants est donc :

$$M^m=M^f+d=28,28+(36,56-31,33)=33,51$$

Etape 2b : Calculer les rapports conditionnels de survie des tables de mortalité pour les hommes

Les rapports de survie sont dans la sixième colonne du tableau 6 ; ils sont calculés à partir des proportions de la quatrième colonne en utilisant les coefficients de régression du tableau 2 et l’estimation de $${\overline{M}}^m$$, égale à 33,51 ans à l’étape 1b. Par exemple, pour les estimations finales du tableau 6 :

$${}_{40}{}^{}p{}_{35}=-0,9950+0,02635\times 33,51+0,4269\times 0,4818+0,8263\times 0,3432=0,3772$$

L’estimation de 0,9336 (à partir des proportions de 0,9622 et 0,8999) et l’estimation de 0,9000 (à partir des proportions de 0,8999 et 0,8394) sont toutes deux des mesures de ₁₅p₃₅, alors que l’estimation suivante, 0,8398, mesure ₂₀p₃₅, et ainsi de suite.

Tableau 6 Estimation de la survie des hommes, des dates auxquelles ces estimations sont localisées dans le temps, et estimations correspondantes de α et ₃₀q₃₀ tirées des proportions d’orphelins de père, Irak, Recensement de 1997, Sexes réunis

Groupe d’âge	Total des femmes	Père vivant	Proportion père vivant	Age n	l (35+n) l (35)	Niveau (α)	Probabilité de décéder  (30q30)	Date
5 - 9	2 834 210	2 727 110	0,9622	15	0,9336	-0,216	0,175	1992,7
10-14	2 391 580	2 152 090	0,8999	15	0,9000	0,045	0,251	1990,6
15-19	2 181 840	1 831 390	0,8394	20	0,8398	0,057	0,254	1988,7
20-24	1 827 030	1 435 320	0,7856	25	0,7707	0,026	0,245	1987,0
25-29	1 615 160	1 127 370	0,6980	30	0,6629	0,043	0,250	1985,5
30-34	1 235 120	726 870	0,5885	35	0,5409	0,025	0,244	1984,6
35-39	788 170	379 770	0,4818	40	0,3772	0,065	0,257	1984,8
40-44	817 460	280 540	0,3432

 

 

Etape 3 : Convertir les rapports de survie en estimations du niveau de mortalité

Les septièmes colonnes des tableaux 4 et 6 contiennent α, le paramètre de niveau du système des tables-types de mortalité logit relationnelles avec comme standard une table-type de mortalité des Nations Unies, réseau Général, pour les deux sexes avec e₀ = 60. Par exemple, α est calculé à partir de l’estimation de ₁₀p₂₅ pour les femmes :

$$\alpha =-\frac{1}{2}\ln \left(1+\frac{\frac{0,9913}{0,8335}-\frac{1}{0,86313}}{1-0,9913}\right)=-0,756.$$

Les huitièmes colonnes des tableaux 4 et 6 contiennent ₃₀q₃₀, la probabilité de décéder entre le 30^ème et le 60^ème anniversaire. Ayant calculé α= -0,756 à partir de ₁₀p₂₅, la mesure correspondante de ₃₀q₃₀ est :

$${}_{30}{}^{}q{}_{30}=1-\frac{1+e^{2(-0,756-0,8655)}}{1+e^{2(-0,756-0,3064)}}=0,072.$$

Etape 4 : Calculer la localisation dans le temps des estimations

Les dates dans les neuvièmes colonnes du tableau 4 et du tableau 6 sont calculées en soustrayant la localisation des estimations dans le temps à la date du recensement de 1997 en Irak, soit le 16 octobre. En numération décimale, cette date devient 1997,79.

La localisation dans le temps de chaque estimation est calculée à partir des âges des répondants, l’estimation appropriée de

$$\begin{array}{c}T=\frac{(10+0,75)}{2}\left(1-\frac{1}{3}\ln (\sqrt{0,9622\cdot 0,8999})+\frac{1}{3}\ln \left(\frac{80-33,51-10}{80-(33,51-0,75)}\right)\right)\\ =\frac{10,75}{2}(1-0,0621)=5,04 .\end{array}$$

La date à laquelle se réfère cette première estimation est donc 1997,79 –5,04 = 1992,75.

La localisation dans le temps de l’estimation de la mortalité des femmes calculée à partir des données fournies par les répondants âgés de 45-49 ans est près de trois ans postérieure à la localisation dans le temps de l’estimation calculée à partir des données des répondants âgés de 40-44 ans. Comme dans de nombreuses applications de la méthode des proportions d’orphelins, les données du groupe d’âge le plus élevé doivent être éliminées.

Diagnostics, analyse et interprétation

Contrôles et validation

Le nombre de répondants qui ont déclaré ne pas savoir si leur mère ou leur père est vivant ou qui n’ont pas répondu à la question doit être vérifié, avant que les données soient retirées en vue de l’analyse. Si ce nombre est important, il se peut que l’information donnée par ceux qui ont répondu à ces questions ne soit pas représentative de l’ensemble de la population. En outre, un taux élevé de non réponse peut indiquer que les enquêteurs ou les répondants ont eu des difficultés avec les questions. Il est alors possible que les réponses, même quand elles ont été fournies, ne soient pas fiables. S’il y a un taux élevé de non réponse à une question, il peut être intéressant de savoir si le défaut est concentré sur une minorité d’enquêteurs ou sur un certain type de répondants.

Si l’information sur la survie des mères et des pères a été obtenue à la fois de répondants hommes et femmes dans un recensement ou une grande enquête avec des marges d’erreur étroites, il est possible d’établir les proportions de pères et de mères encore en vie séparément pour les répondants de chaque sexe en vue de comparer la cohérence des déclarations. La cohérence des déclarations ne garantit pas leur exactitude, mais des différences statistiquement significatives entre les proportions calculées pour les répondants hommes et femmes impliquent qu’au moins un des deux sexes, et peut-être les deux, donnent des réponses inexactes.

Il est courant de constater que les femmes déclarent des proportions de parents vivants plus basses que les hommes. Certains analystes pensent que c’est parce que les femmes restent en contact plus étroit que les hommes avec leurs parents et que certains hommes disent que leurs parents sont en vie parce qu’ils ne savent pas qu’ils sont en fait décédés. Si c’est vrai, les données des femmes sont plus exactes que celles des hommes. Mais il n’y a pas de preuve convaincante qui confirme cette interprétation et d’autres facteurs, en particulier les différences entre hommes et femmes dans les erreurs sur la déclaration de leur âge, peuvent aussi être à l’origine des incohérences dans les proportions déclarées par les hommes et les femmes. De plus, dans les enquêtes ne portant que sur quelques milliers de ménages, les marges d’erreur des estimations pour les premiers groupes d’âge peuvent être larges par rapport aux proportions de mères ou de pères décédés. S’il n’y pas de raison particulière pour privilégier les réponses des femmes, nous conseillons donc d’établir les estimations finales de la mortalité adulte sur les réponses combinées des deux sexes.

Interprétation

Les résultats de l’analyse des données sur les proportions d’orphelins tirées du recensement de 1997 en Irak sont représentés graphiquement sur la figure 1. Il ne s’agit pas simplement d’interpréter ces courbes en lisant des tendances, mais de faire le partage entre ce qui reflète des évolutions réelles de la mortalité et ce qui tient à des problèmes de données ou de méthode.

Dans cette application de la méthode, les estimations tirées des données fournies par les répondants hommes et femmes sont semblables, ce qui rassure sur la qualité à la fois de la déclaration des âges et des déclarations sur la survie des parents en Irak. Néanmoins, les femmes adultes sont un peu moins enclines à déclarer leur père vivant que les hommes adultes du même âge et l’ampleur de cette incohérence dans les déclarations s’accentue à mesure que l’âge des répondants augmente. Cet écart est à l’inverse de ce qu’on observe dans la plupart des populations. On pourrait l’expliquer par une tendance à surestimer leur âge plus forte chez les femmes que chez les hommes, ou une tendance à le sous-estimer plus forte chez les hommes que chez les femmes, mais ces deux schémas d’erreur semblent peu vraisemblables. Autre explication possible : certains hommes adultes pourraient avoir déclaré décédé leur père survivant ou certaines femmes pourraient avoir déclaré vivant leur père décédé. Cette dernière possibilité est peut-être la plus plausible des quatre explications, mais il n’y a pas de preuve solide pour la confirmer. Le plus raisonnable consiste peut-être à supposer que les déclarations des hommes et des femmes sont légèrement biaisées dans des sens opposés et à utiliser les estimations calculées sur les répondants des deux sexes réunis.

 

Image

Figure 1 Trends in the probability of dying between exact ages 30 and 60 estimated from orphanhood, Iraq, 1997 Census

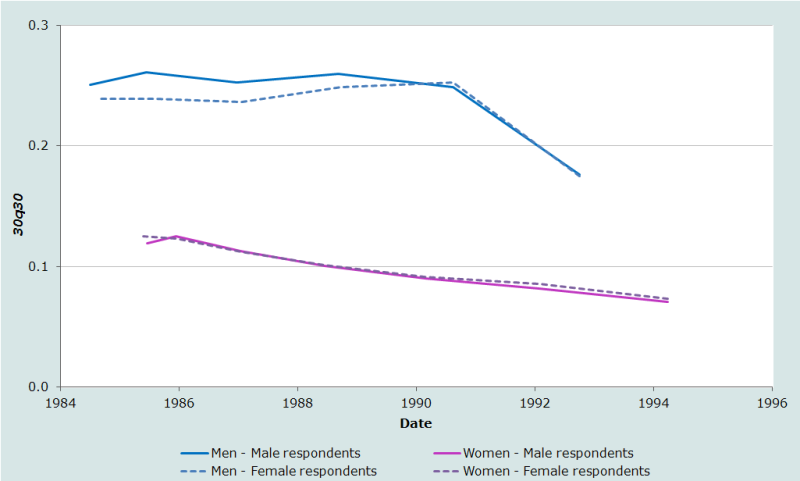
Quelle que soit la série de données qu’on choisisse, les estimations des proportions d’orphelins suggèrent un recul constant de la mortalité des femmes adultes en Irak entre le milieu des années 1980 et le milieu des années 1990, le niveau atteint à cette dernière date étant à peine supérieur à celui dans la plupart des pays occidentaux. La régularité de la tendance est rassurante mais le bas niveau de la mortalité est étonnant. Sans autre donnée pour corrobore ces résultats, on accueillera ceux-ci avec réserve car ils pourraient être sous-estimés, les décès de certaines mères pouvant avoir été omis, en particulier ceux qui se sont produits lorsque les répondants étaient de jeunes enfants. Ceci tend à exagérer l’impression de baisse de la mortalité.

La mortalité des hommes adultes est estimée à un niveau bien supérieur à celle des femmes. Les résultats suggèrent en outre une stagnation de la mortalité masculine pendant la plupart des années 1980, avant une baisse rapide au début de la décennie suivante. Il est vraisemblable que ce schéma reflète l’impact sur les proportions d’orphelins des pertes durant la guerre Iran-Irak de 1980-1988, au cours de laquelle un quart à un demi million de soldats irakiens sont sans doute décédés. Les statistiques d’état civil font généralement la distinction entre les décès civils et militaires, mais pas les données de recensement et d’enquête, qui les font apparaître ensemble. L’estimation la plus récente sous-estime sans doute la mortalité des hommes du fait d’une sous-déclaration des pères décédés, mais il se peut qu’elle soit largement inférieure aux autres car près de la moitié des répondants sur la déclaration desquels elle s’appuie sont nés après la fin de la guerre. C’est pourquoi leur père a de grandes chances d’avoir survécu. En revanche, toutes les autres estimations sont fondées sur les déclarations de répondants nés avant 1988. Les pères des répondants âgés de 30-39 ans, qui ont fourni l’information utilisée dans l’estimation la plus ancienne, avaient environ 50 ans en moyenne au début de la guerre. La plupart d’entre eux étaient trop âgés pour être envoyés au front.

Il faut cependant rappeler que la méthode des proportions d’orphelins tend à lisser les fluctuations de la mortalité, puisque chaque estimation est fondée sur les décès survenus sur l’ensemble des années séparant la naissance des répondants de la date à laquelle les données sont recueillies. En outre, la tendance estimée peut être quelque peu déformée si la table-type de mortalité adoptée pour le calcul de ₃₀q₃₀ est inappropriée. Ces résultats ne peuvent donc par être interprétés comme s’ils reflétaient précisément l’évolution de la mortalité masculine en Irak entre le début des années 1980 et le début des années 1990. Il se peut par exemple que la mortalité des hommes ait augmenté quelque peu avant de baisser, ou qu’elle ait fluctué fortement d’une année à l’autre pendant la guerre, en fonction du nombre des victimes.

Description détaillée de la méthode

Introduction

L’usage de l’information sur les parents décédés pour une estimation de la mortalité adulte a d’abord été envisagé par Louis Henry (1960). Si la survie peut être considérée comme une fonction linéaire de l’âge, la proportion d’enfants orphelins à tout âge x, O(x), dépend, à très peu près, de la probabilité de survivre entre l’âge moyen ($$\overline{M}$$) des parents à la naissance de leurs enfants et l’âge $$\overline{M}+x$$. Cependant, cette relation sous-estime le rapport de survie ($${}_{x}p{}_{\overline{M}}$$) car l’accroissement des taux de mortalité avec l’âge est rapide et la courbe de survie aux âges adultes, convexe. Le faible risque de décéder de ceux qui ont leurs enfants jeunes ne suffit pas à compenser le risque élevé de ceux qui ont leurs enfants relativement tard. Pour en tenir compte, Henry a proposé un ajustement fondé sur la variance des âges à la naissance des enfants.

La mise au point ultérieure de méthodes simples et robustes pour estimer la mortalité à partir des proportions d’orphelins doit beaucoup à William Brass. Hill et Blacker ont aussi joué un rôle important en établissant des moyens d’estimer la mortalité des hommes à partir des proportions d’orphelins de père. Le développement de la procédure est passé par un certain nombre d’étapes, plusieurs variantes ont circulé de manière informelle et ont finalement été publiées dans Brass (1975). La version ultime de la méthode de Brass est, toutefois, celle publiée dans Brass et Hill (1973). Elle consiste à calculer des mesures de la survie dans la table de mortalité comme une moyenne pondérée des proportions de répondants ayant des parents encore en vie dans deux groupes d’âge contigus, les pondérations étant déterminées par l’âge moyen à la naissance des enfants ($$\overline{M}$$) dans la population, et permettant d’introduire un ajustement qui en tient compte.

Par la suite, plusieurs chercheurs ont proposé des méthodes de régression pour prédire la mortalité des femmes à partir des proportions de répondants dont la mère survit (Hill and Trussell 1977; Palloni and Heligman 1985). Timæus (1992) a démontré que les facteurs de pondération tendent à sous-estimer la mortalité quand celle-ci est supérieure au standard utilisé pour les calculer et à surestimer la mortalité quand elle est inférieure au standard. Une approche par la régression doit généralement donner des estimations plus précises, en particulier de la mortalité des hommes, car le terme constant introduit une flexibilité supplémentaire permettant de modéliser plus précisément la relation entre la survie des parents et la fonction de survie des tables de mortalité à différents niveaux d’espérance de vie. C’est pourquoi Timæus (1992) a proposé des coefficients de régression pour la mortalité des hommes, ainsi que des coefficients obtenus à partir d’hypothèses cohérentes pour l’estimation de la mortalité des femmes. C’est cette variante de la méthode des proportions d’orphelins qui est présentée ici.

Exposé mathématique de la méthode des proportions d’orphelins

Soit _aV_y le nombre d’enfants nés a années avant un recensement ou une enquête, issus de femmes âgées de y au moment de la naissance de l’enfant. La probabilité que les enfants soient encore en vie au moment d’être interrogés est $$l(a)$$ et la probabilité que leur mère soit encore envie est $$l(y+a)/l(y)$$. Si on suppose que la mortalité des orphelins est égale à celle des enfants ayant encore leurs parents, la proportion de répondants âgés de a ayant encore leur mère, S(a), est

$$S(a)=\frac{l(a){\displaystyle \underset{s}{\overset{\omega }{\int }}{}_{a}V{}_{y}l(y+a)/l(y)dy}}{l(a){\displaystyle \underset{s}{\overset{\omega }{\int }}{}_{a}V{}_{y}dy}}$$

où les intégrales sont prises sur l’ensemble des âges à la naissance des enfants, de s à ω.

Le nombre d’enfants nés de femmes âgées de y est une fonction du nombre de femmes âgées de y et du taux de fécondité à l’âge y. Si nous supposons une structure par âge stable, on a

$${}_{a}V{}_y=B(0)e^{-r(y+a)}\text{l}(y)f(y)$$

où r est le taux d’accroissement naturel et f(y) est le taux de fécondité des mères à l’âge y. C’est pourquoi, la proportion de répondants dans un groupe quinquennal d’âge de x à x + 5 ayant leur mère encore en vie est

$${}_{5}S{}_x=\frac{{\displaystyle \underset{x}{\overset{x+5}{\int }}{e}^{-ra}l(a){\displaystyle \underset{s}{\overset{\omega }{\int }}{e}^{-ry}f(y)l(y+a)dy}da}}{{\displaystyle \underset{x}{\overset{x+5}{\int }}{e}^{-ra}l(a){\displaystyle \underset{s}{\overset{\omega }{\int }}{e}^{-ry}f(y)l(y)dy}da}}$$

L’exposition des pères va de la conception des répondants à leur âge actuel. La prise en compte du fait qu’un père peut décéder entre la conception et la naissance de son enfant rend un peu plus compliquée l’équation de la proportion de répondants dans un groupe quinquennal d’âge de x à x + 5 ayant leur père encore en vie :

$${}_{5}S{}_x=\frac{{\displaystyle \underset{x}{\overset{x+5}{\int }}{e}^{-ra}l(a){\displaystyle \underset{s}{\overset{\omega }{\int }}{e}^{-ry}f(y)l(y)l(y+a)/l(y-0.75)dy}da}}{{\displaystyle \underset{x}{\overset{x+5}{\int }}{e}^{-ra}l(a){\displaystyle \underset{s}{\overset{\omega }{\int }}{e}^{-ry}f(y)l(y)dy}da}}$$

Dans cette équation, f(y) représente le schéma de fécondité par âge, et l(a) la fonction de survie de la table de mortalité, pour les hommes au lieu des femmes et les âges entre lesquels la naissance des enfants survient, s et ω, sont aussi les âges des hommes. Il n’y a pas de façon simple d’intégrer le numérateur ou le dénominateur de ces expressions de ₅S_x, qui doivent donc être évaluées numériquement.

Mise en œuvre de la méthode

En principe, rien n’empêche de résoudre l’équation 1 directement pour déterminer la fonction de survie de la table de mortalité, en utilisant le solveur d’Excel ou un outil équivalent et une structure par âge appropriée pour ceux qui donnent naissance aux enfants _aV_y. Pour obtenir une solution unique, il faut encore faire une hypothèse sur le schéma par âge de la mortalité adulte, par exemple en adoptant un système à 1 paramètre de tables-types de mortalité relationnelles. En pratique, les estimations sont généralement obtenues à partir d’un modèle de régression qui prend en compte $$\overline{M}$$, lequel a été ajusté à des données simulées sur la survie des parents, générées pour des populations ayant un large éventail de structures par âge et de profils de fécondité et de mortalité (Timæus 1992). 

Les proportions de mères encore en vie dans les groupes d’âge de x à x + 5 sont plus étroitement corrélées à la survie des femmes dans l’intervalle d’âge entre 25 ans et x + 5 qu’à tout autre rapport de survie, aussi cette mesure peut elle être estimée plus précisément que toute autre à partir des proportions de mères survivantes :

$${}_{n}p{}_{25}=a(n)+b(n){\overline{M}}^f+c(n){}_{5}S{}_{n-5}$$

En particulier dans les populations de fécondité basse et d’âge moyen élevé à la naissance des enfants, la précision des estimations est augmentée significativement si on estime la survie à partir des proportions de pères encore en vie dans deux groupes d’âge contigus. Le groupe d’âge supplémentaire saisit les effets des variations du taux auquel la mortalité augmente avec l’âge. A la plupart des âges, les proportions de pères encore en vie dans les groupes d’âge de x à x + 10 sont plus étroitement corrélées à la survie des hommes dans l’intervalle d’âge entre 35 ans et x + 5 qu’à tout autre rapport de survie. L’équation de régression est donc

$${}_{n}p{}_{35}=a(n)+b(n){\overline{M}}^m+c(n){}_{5}S{}_{n-5}+d(n){}_{5}S{}_n$$

Les deux premiers groupes d’âge, les répondants âgés de 5-9 et 10-14 ans, prédisent la survie de 35 à 50 ans plus précisément que de 35 à 45 ans. L’équation devient donc

$${}_{15}p{}_{35}=a(10)+b(10){\overline{M}}^m+c(10){}_{5}S{}_5+d(n){}_{5}S{}_{10}$$

Exposé mathématique – localisation des estimations dans le temps

L’équation 1 peut être récrite comme une moyenne pondérée des rapports de survie dans les cohortes :

$$S(a)={\displaystyle \underset{s}{\overset{\varpi }{\int }}{}_{a}v{}_y{}_{a}p{}_y^{c}dy}$$

où

$${}_{a}v{}_y=\frac{{}_{a}V{}_y}{{\displaystyle \underset{s}{\overset{\omega }{\int }}{}_{a}V{}_{y}dy}}$$.

Ainsi, _av_y représente la contribution faite à S(a), proportion de parents adultes survivant a années, par les parents qui ont commencé leur exposition au risque à l’âge y. Les méthodes de localisation dans le temps visent à estimer le temps T, où les mesures de la survie des cohortes qui ont permis de calculer la proportion de parents survivants, $${}_{a}p{}_y^c$$, sont égales aux mesures du moment équivalentes, _ap_y(T), de sorte que

$$S(a)={\displaystyle \underset{s}{\overset{\varpi }{\int }}{}_{a}v{}_y{}_{a}p{}_y(T)dy}$$

Si nous notons _ag_y la durée moyenne écoulée depuis le décès des personnes décédées entre y et y + a , par définition

$${}_{a}g{}_y=\frac{{\displaystyle \underset{y}{\overset{y+a}{\int }}\left(z-y-a\right)\mu (z)l(z)dz}}{{\displaystyle \underset{y}{\overset{y+a}{\int }}\mu (z)l(z)dz}}$$

où $$\mu (z)l(z)$$ désigne les décès de la table de mortalité à l’âge z. Brass et Bamgboye (1981) montrent que, si les profils de mortalité sont conformes à un système de tables-types de mortalité logit relationnelles à 1 paramètre (Brass 1971), et si on peut supposer l’évolution de la mortalité linéaire en α, le paramètre de ce système de tables-types, alors la date à laquelle la survie des adultes par cohorte est égale à la survie du moment est une moyenne pondérée des durées écoulées depuis le décès des parents du répondant.

$$T=\frac{{\displaystyle \underset{x}{\overset{x+5}{\int }}l(a){\displaystyle \underset{s}{\overset{\omega }{\int }}{}_{a}v{}_{y}l(y+a,T)\left(1-{}_{a}p{}_y(T)\right){}_{a}g{}_y}}dyda}{{\displaystyle \underset{x}{\overset{x+5}{\int }}l(a){\displaystyle \underset{s}{\overset{\omega }{\int }}{}_{a}v{}_{y}l(y+a,T)\left(1-{}_{a}p{}_y(T)\right)}}dyda}$$

Cette localisation dans le temps dépend du niveau de la mortalité et des âges des parents, mais elle est indépendante du taux de variation en α. Pour établir l’équation 3, Brass et Bamgboye tirent parti d’une relation entre les variations de la mortalité au fil des âges et au fil du temps qui est propre au système logit relationnel de tables-types, mais il est possible d’arriver à des formules similaires pour T sur la base d’autres hypothèses raisonnables sur l’évolution dans le temps de la mortalité par âge (Palloni, Massagli and Marcotte 1984).

L’équation 3 peut être évaluée numériquement, en utilisant des valeurs de _av_y et pour des mesures de la table de mortalité choisies sur la base de données observées. Pour développer une procédure aisée d’estimation de T à partir des caractéristiques observées d’une population, il faut supposer une relation beaucoup plus simple que celle décrite par l’équation 3. Brass et Bamgboye (1981) font valoir que la variation de T avec a dans des intervalles d’âge limités est suffisamment proche de la linéarité pour que tous les répondants dans un groupe quinquennal d’âge puissent être traités comme regroupés à l’âge central N. Ils font valoir ensuite qu’aux âges et aux niveaux de mortalité où les méthodes indirectes sont utilisées pour estimer la mortalité adulte, la force de mortalité s’accroit à peu près exponentiellement avec l’âge. En conséquence, pour de telles applications, la variation de _ag_y avec y est insignifiante. C’est pourquoi les facteurs de pondération de _ag_y dans l’équation 2 ont peu d’effet et tous les parents adultes peuvent être traités comme si leur exposition au risque débutait à leur âge moyen à l’entrée, M. D’où l’approximation satisfaisante,

$$T={}_{N}g{}_M$$

Si la survie des adultes recule linéairement avec l’âge, de sorte que le même nombre de décès survienne à chaque âge, alors _Ng_M est égal à N/2 quelle que soit la valeur de M. Dans des tables de mortalité moins extrêmes, la mortalité s’accroit avec l’âge plus rapidement que cela et les décès des parents sont concentrés aux âges avancés et, en conséquence, dans la portion récente de la période de N années. Ceci signifie que la localisation dans le temps des estimations est plus proche de l’enquête que N/2. En remplaçant $$\mu (z)l(z)$$ par $$e^{kz}\mu (y)l(y)$$ dans l’équation 2 et en développant la partie droite en puissances de N, Brass et Bamgboye (1981) démontrent que l’ajustement approprié pour _Ng_M est une fonction du niveau de mortalité tel que mesuré par k et de l’âge des répondants mesuré par N :

$${}_{N}g{}_M\approx \frac{N}{2}\left(1-\frac{kN}{6}\right)$$

 

Brass et Bamgboye (1981) démontrent aussi que l’hypothèse d’une augmentation exponentielle de la mortalité avec l’âge implique que, dans un système de tables de mortalité logit relationnel :

$$\frac{e^{kN}}{e^{k_{s}N}}=\frac{{\left({}_{N}p{}_M\right)}^2}{{\left(l_s(M+N)/l_s(M)\right)}^2}$$

En résolvant pour kN et en replaçant cette expression dans l’équation 4, on obtient une estimation de _Ng_M et donc de T :

$$T=\frac{N}{2}\left(1-\frac{\ln \left({}_{N}p{}_M\right)}{3}+\frac{1}{3}\ln \left(\frac{l_s(M+N)}{l_s(M)}\right)-\frac{k_{s}N}{6}\right)$$

Dans cette formulation, les localisations dans le temps des mesures de survie conditionnelle tirées des données sur les parents adultes sont estimées à la moitié de la durée d’exposition, N, réduite par un facteur qui dépend du niveau de la survie conditionnelle comparé au niveau de la survie dans une table de mortalité standard.

Ayant obtenu cette expression de T sur une base théorique, Brass (1985) approxime _Np_M par ₅S_x et adopte comme standard une table de mortalité où $$l_s(x)$$ est linéaire aux âges adultes et est pris égal à (1 – x/80)/2. Comme $$l_s(x)$$ est linéaire, T = ½N et k_s devient nul. T est donc estimé à partir des données observées grâce à

$$T=\frac{N}{2}\left(1-\frac{\ln \left({}_{5}S{}_x\right)}{3}+\frac{1}{3}\ln \left(\frac{80-M-N}{80-M}\right)\right)$$

L’accord entre les estimations de T obtenues par cette procédure simplifiée et celles obtenues en calculant l’équation 2 est très étroit jusqu’à ce que l’âge des parents, M + N, atteigne 75 ans. Mais à mesure que M + N s’accroit, le schéma par âge de la mortalité commence à avoir un effet important sur la durée moyenne écoulée depuis les décès des parents adultes, _Ng_M. Par exemple, si la force de mortalité s’accroit relativement lentement avec l’âge par rapport au standard, une proportion élevée de parents décédés seront morts il y a relativement longtemps. S’il y a des signes d’existence d’un tel schéma de mortalité par âge ou d’un schéma opposé, il est possible d’en tenir compte en définissant un standard plus approprié en modifiant β, le second paramètre dans un système logit relationnel de tables de mortalité (Brass 1971). Dans ce cas, $$l_s(x)$$ n’est plus linéaire avec l’âge dans la table retraçant une mortalité forte utilisée comme standard et le terme en ks dans l’équation 5 doit être retranché des estimations de T tirées de l’équation 6. En faisant les mêmes hypothèses que précédemment sur la forme de, l’ajustement est :

$$\delta T=-\frac{N}{12}\left(\beta -1\right)\ln \left(\frac{\left(80-M\right)\left(80+M+N\right)}{\left(80+M\right)\left(80-M-N\right)}\right)$$

Quand on utilise l’équation 6 pour calculer la localisation dans le temps des estimations de la mortalité féminine à partir de données sur la survie de la mère, ₅S_x devient ₅S_n-5, la proportion de répondants dont la mère est encore en vie, N est le point médian de ce groupe d’âge, n – 2,5  et

$$M=\overline{M}$$

est l’âge moyen des femmes à la naissance de leurs enfants. Quand on calcule la localisation dans le temps des estimations de la mortalité masculine à partir des données sur la survie des pères, ₅S_x est la proportion des répondants dont le père est encore en vie, M devient l’âge moyen des pères à la conception de leurs enfants ; et N = n + 0,75 où n est l’âge qui sépare les deux groupes d’âge, ₅S_n-5 et ₅S_n, qui contribuent à l’estimation de la survie des hommes. Afin de centrer ₅S_x sur l’âge n, il est calculé comme

$${}_{5}S{}_x=\sqrt{{}_{5}S{}_{n-5}\cdot {}_{5}S{}_n}$$

Extensions de la méthode

Proportions d’orphelins dans des populations affectées par le sida

Les estimations de mortalité obtenues par la méthode des proportions d’orphelins peuvent être affectées par des biais importants dans les populations soumises à une épidémie généralisée de VIH. Premièrement, les femmes séropositives ont une fécondité moindre que les femmes non infectées, pour des raisons à la fois comportementales et biologiques. Deuxièmement, les femmes séropositives peuvent transmettre le virus à leur enfant durant la grossesse, à l’accouchement et pendant qu’elles l’allaitent. Il en résulte que les femmes infectées par le VIH, qui ont un risque de décéder élevé, tendent à avoir moins d’enfants vivants que la population en général. La proportion de mères encore en vie se trouve de ce fait surestimée. Comme les femmes risquent d’avoir été infectées par ou d’infecter leur mari, les estimations de la mortalité masculine fondée sur les proportions d’orphelins dans les populations affectées par le VIH sont également biaisées vers le bas, quoique dans une moindre mesure que les estimations de la mortalité féminine. Un troisième biais important lié au VIH dans les estimations par les proportions d’orphelins tient à ce que les coefficients utilisés pour convertir des proportions de parents encore en vie en indices conventionnels des tables de mortalité postulent un schéma par âge de la mortalité adulte très différent de celui qu’on observe dans les populations atteintes par une épidémie de Sida.

 

Ajustement pour tenir compte du biais de sélection lié au VIH

Si on dispose d’estimations des caractéristiques pertinentes de l’épidémie de VIH dans une population au moment de la naissance des répondants, on peut tenir compte des deux premiers biais en ajustant à la baisse les proportions déclarées de mères encore en vie (Timæus and Nunn 1997). La procédure d’ajustement inclut l’hypothèse selon laquelle la plupart des individus déjà infectés par le VIH au moment de la naissance de leurs enfants vont décéder en quelques années. Cette hypothèse était raisonnable avant que des traitements soient répandus à grande échelle, mais elle a rapidement cessé de l’être après leur diffusion massive. En fait, si ces programmes se révèlent capables de réduire la mortalité des adultes séropositifs à un niveau proche de celui de la population générale, il n’y aura plus besoin d’ajustement.

Pour ajuster les données recueillies dans les recensements réalisés vers 2010 ou antérieurement, on doit disposer d’estimations de la prévalence de l’infection par VIH parmi les femmes fréquentant les consultations prénatales (P), le taux de transmission verticale du VIH (h), c'est-à-dire la proportion d’enfants qui reçoivent le VIH de leur mère, et le niveau relatif de la fécondité des femmes séropositives comparée à celle des femmes séronégatives (F). De ces mesures, (Timæus and Nunn 1997) tirent un facteur correctif pour ajuster les proportions déclarées de répondants ayant leur mère encore en vie ($${}_{5}S{}_x^{*}$$) et obtenir les proportions qui seraient déclarées si les femmes séropositives avaient autant d’enfants que les autres femmes (₅S_x) :

$${}_{5}S{}_x=\frac{1-hP}{1+\frac{1-F}{F}P}{}_{5}S{}_x^{*}$$

Le facteur correctif est fondé sur l’idée que le biais dans la proportion déclarée de répondants ayant leur mère encore en vie s’accroit avec la prévalence du VIH à un taux déterminé par F et h. Comme on peut s’y attendre, plus le taux de transmission verticale est élevée et plus est faible la fécondité des femmes infectées, plus est important le biais dans les déclarations de la survie des mères. Quoique F, P et peut-être h varient avec l’âge de la mère, la comparaison des résultats de cet ajustement brut avec ce qu’on obtient par des calculs détaillés par âge suggère que la précision de l’ajustement brut est suffisante (Timæus and Nunn 1997).

Si le traitement par les antirétroviraux ne bénéficie qu’à très peu, voire aucune des personnes infectées par le VIH, comme c’était le cas dans les populations africaines au XXe siècle, la transmission verticale est généralement de l’ordre de 25 à 40 %, en moyenne un tiers (De Cock, Fowler, Mercier et al. 2000). Mais les programme de prévention de la transmission mère-enfant (PTME) ont déjà réduit ce taux d’environ un quart dans les pays de forte prévalence et pourraient même l’amener à moins de 8 % dans les pays pauvres (Mahy, Stover, Kiragu et al. 2010). La réduction de la fécondité des femmes infectées est généralement d’environ 25 % dans les populations où peu d’adultes reçoivent des antirétroviraux, mais on ne sait pas bien comment cela pourrait évoluer à l’avenir (Chen and Walker 2010). Pour les déclarations des répondants nés avant la diffusion des programmes PTME, un ajustement adéquat pourrait être :

$${}_{5}S{}_x=\frac{1-\frac{P}{3}}{1+\frac{P}{3}}{}_{5}S{}_x^{*}$$

Si la prévalence de l’infection VIH était à l’époque de 7 % parmi les femmes fréquentant des consultations prénatales, ceci devient

$${}_5{}^{}S{}_x=\frac{1-0,0233}{1+0,0233}{}_5{}^{}S{}_x^{*}=0,954{}_5{}^{}S{}_x^{*}$$

La correction des proportions de répondants déclarant que leur père est encore en vie est plus difficile. L’ajustement à la baisse dépend de la proportion d’hommes infectés avec des partenaires infectées. Malheureusement, cette statistique est rarement connue et les observations disponibles suggèrent qu’elle varie fortement d’une population à l’autre, de sorte que l’utilisation d’une valeur moyenne donne des résultats plutôt imprécis (de Walque 2007; Freeman and Glynn 2004; Kaiser, Bunnell, Hightower et al. 2011). En outre, il n’a pas été démontré qu’un facteur correctif brut ignorant des différences des paramètres liées à l’âge fonctionne correctement pour les données relatives aux pères. Néanmoins, les proportions ajustées sont généralement moins biaisées que les proportions non ajustées dans les populations où l’épidémie est sévère. Si w est la proportion d’hommes avec des partenaires infectées, le facteur d’ajustement approprié est :

$${}_{5}S{}_x=(1-(1-(1-h)F)(1-w)P^{*}){}_{5}S{}_x^{*}$$

où P* est une estimation de la prévalence du VIH chez les hommes dans la population générale, par opposition à l’estimation chez les femmes, établie dans les consultations prénatales. Par exemple, pour h = 1/3, F = 0,75, w = 0,5 et P* = 0,05 on obtient

$${}_5{}^{}S{}_x=(1-(1-(1-0,3333)0,75)(1-0,5)0,05){}_5{}^{}S{}_x^{*}=0,9875{}_5{}^{}S{}_x^{*}$$

Pour les répondants âgés de moins de 15 ans, l’hypothèse que tous les parents infectés au moment de la naissance des répondants sont déjà décédés est irréaliste, même dans les données recueillies avant la mise en place de programmes de traitement de masse. Environ la moitié de ce groupe de parents est encore en vie chez les répondants de 5-9 ans et peut-être un quart chez les 10-14 ans. S’il en va ainsi, la correction (c'est-à-dire 1 moins le facteur correctif) faite sur les données des répondants de 5-9 ans doit être réduite de moitié et celle des répondants de 10-14 ans, d’un quart.

Coefficients révisés pour l’estimation de la mortalité féminine

Timæus et Nunn (1997) ont aussi développé une nouvelle série de coefficients de régression pour estimer les survivants de la table de mortalité à partir des proportions de répondants dont la mère est vivante, dans des populations subissant une épidémie sévère de VIH (voir tableau 7). Ces coefficients sont destinés à des populations où la prévalence de l’infection VIH chez les adultes atteint ou dépasse 5 %. Le modèle de régression est le même que dans le cas standard et les coefficients ne diffèrent que pour les répondants âgés de moins de 30 ans :

$${}_{n}p{}_{25}=a(n)+b(n){\overline{M}}^f+c(n){}_{5}S{}_{n-5}$$

Des coefficients équivalents n’ont pas été développés pour l’estimation de la mortalité masculine, car on sait peu de choses sur les interrelations entre les schémas par âge de l’incidence du VIH et de la fécondité.

Tableau 7 Coefficients pour l’estimation de la survie des femmes à partir des proportions de répondants dont la mère survit dans des populations subissant une épidémie généralisée de VIH

n	a(n)	b(n)	c(n)
10	-0,3611	0,00125	1,2974
15	-0,4030	0,00222	1,3732
20	-0,2120	0,00372	1,1342
25	-0,2389	0,00586	1,1131
30	-0,2513	0,00885	1,0223
Source: Timæus and Nunn (1997)

On en sait davantage aujourd’hui que dans les années 1990 sur les schémas par âge de l’incidence du VIH, sur la survie post-infection et sur le schéma par âge des réductions de la fécondité chez les personnes infectées. Les coefficients du tableau 7 pourraient surement être améliorés. Mais ils ne sont sans doute pas fortement biaisés. Ils sont néanmoins probablement inappropriés dans des populations où le traitement par les antirétroviraux s’est largement diffusé auprès des adultes infectés par le VIH.

Estimation du niveau et de l’évolution de la mortalité

Le défi le plus important dans l’estimation de la mortalité adulte à partir des proportions d’orphelins, dans des populations subissant une épidémie généralisée de sida, est l’absence de système adéquat de tables-types de mortalité reproduisant les schémas par âge de mortalité caractéristiques de séries de populations subissant des épidémies de sida à divers degrés de sévérité. Comme les décès dus au sida sont concentrés chez les adultes entre 25 et 55 ans environ, les variations du niveau de mortalité résultant de la diffusion du VIH modifient aussi radicalement le schéma par âge de la mortalité. Ceci réduit grandement la confiance avec laquelle on peut passer de mesures de la survie dans différents intervalles d’âge à un indice commun de mortalité. De plus, comme l’incidence de l’infection par VIH dans la plupart des populations touchées s’est d’abord accrue rapidement, avant de diminuer aujourd’hui, il peut être approprié d’utiliser différents modèles pour différentes cohortes de répondants. Le fichier Excel comprend des standards de mortalité élaborés pour des populations subissant une épidémie de VIH modérée. Mais ceux-ci ne seront pas adaptés ni aux pays où la prévalence de l’infection par VIH chez les adultes est seulement de quelques pourcents, ni aux pays où l’épidémie est sévère. Il se peut même que les standards soient mal adaptés aux pays où l’épidémie est modérée.

Illustration

Le problème que rencontre l’analyste est illustré par les estimations de la survie adulte faites pour le Kenya, à partir des données du recensement de 1999 sur les proportions d’orphelins représentées figure 2. Les estimations standards, faites sans recours à aucun des ajustements qu’on vient de présenter et traduites en un indice commun de mortalité grâce au réseau Général des tables-types de Nations Unies, sont représentées par la courbe en traits continus. Elles font apparaître une hausse continue, entre environ 1987 et 1996, aussi bien pour les hommes que les femmes, de la probabilité de décéder entre 30 et 60 ans (₃₀q₃₀), une hausse d’environ 10 points de pourcentage dans chaque cas au cours de la décennie.

Les estimations dites ‘standard sida’ ont été obtenues exactement de la même façon, sauf qu’elles ont été converties en estimations de ₃₀q₃₀ grâce à des standards incorporant la mortalité par Sida. Les résultats sont très différents : la mortalité des hommes apparaît comme continuant à décroitre lentement au Kenya jusqu’au début des années 1990, alors que le reste de la mortalité adulte stagne.

Les estimations intitulées ‘Sida’ révèlent l’effet additionnel quand on ajuste les proportions pour tenir compte du biais de sélection dû au Sida et, pour l’estimation féminine la plus récente, quand on utilise les coefficients destinés aux populations où la prévalence de l’infection par VIH chez les adultes dépasse 5 %. Pour les répondants âgés de 5-9 ans, l’ajustement pour tenir compte du biais de sélection et l’utilisation des nouveaux coefficients entrainent tous les deux une hausse substantielle de l’estimation de la mortalité féminine. L’épidémie du VIH au Kenya dans les années 1990 n’était cependant pas assez sévère pour affecter les autres estimations.

 

Image

Figure 2 Trends in the probability of dying between exact ages 30 and 60 estimated from orphanhood, Kenya, 1999 Census

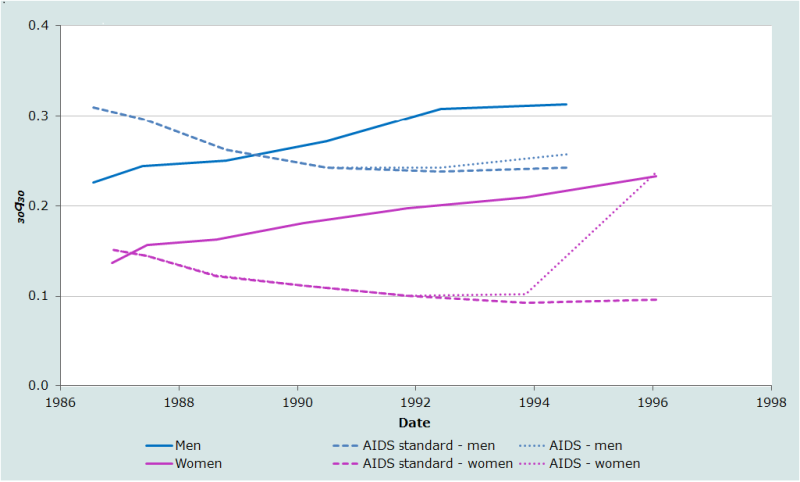
Utiliser le réseau Général des tables-types des Nations Unies pour estimer ₃₀q₃₀, au Kenya pour les années 1990, revient en effet à supposer que les hausses de la mortalité par Sida affectant les jeunes adultes se sont accompagnées de hausses comparables de la mortalité chez les individus d’âge moyen. Ceci semble peu vraisemblable. Les estimations de ₃₀q₃₀ s’appuyant sur les standards Sida impliquent, au contraire, que toute hausse de la mortalité des jeunes adultes a été plus que compensée par un recul continu des taux de mortalité des adultes d’âge moyen, à la fin des années 1980, et compensée plus ou moins exactement par ces reculs, jusque vers 1993. Rares sont cependant les parents de répondants eux-mêmes dans la trentaine en 1999 à risquer d’avoir contracté le VIH, aussi l’utilisation du standard Sida pour faire les premières estimations de ₃₀q₃₀ semble-t-elle également inappropriée. Le scenario peut-être le plus vraisemblable est que la probabilité de décéder entre 30 et 60 ans a stagné entre les fin des années 1980 et le milieu des années 1990 et a commencé ensuite à augmenter, mais sans doute moins abruptement que ne l’indique la courbe ‘Sida’ pour les femmes.

Un point crucial est à souligner : à partir de ces données, il est impossible de déterminer exactement ce qui est arrivé à la mortalité adulte au Kenya pendant les années 1990. Les seules estimations qui soient suffisamment fiables sont relatives à la fin des années 1980. Les résultats sont fondés sur des groupes d’âge ne nécessitant qu’un ajustement limité des proportions des parents encore en vie afin d’estimer ₃₀q₃₀. Les séries s’appuyant sur différents standards se recoupent à cette période.

Devenir orphelin avant ou après son mariage

Il existe des méthodes pour estimer la mortalité adulte à partir des proportions d’orphelins, quand des questions supplémentaires sont posées dans une enquête unique sur la position des décès des parents par rapport au premier mariage des répondants (Timæus 1991). Deux objectifs sous-tendent ces méthodes. Le premier est de fournir des méthodes où la localisation des résultats dans le temps est plus précise qu’avec les méthodes originelles. Le second est de développer des méthodes qui soient moins sujettes au biais de sous-déclaration des proportions d’orphelins aux jeunes âges. Le mariage est un événement qui distingue, pour les répondants de chaque groupe d’âge, entre les décès parentaux récents et ceux survenus il y a longtemps. L’information sur le calendrier des décès est moins précise que celle résultant de questions directes sur la date de décès des parents, mais elle peut aussi être plus fiable. Même si les répondants ne peuvent pas se souvenir précisément de la date de décès de leurs parents, sans doute que presque tous sont capables de situer les décès de leurs parents par rapport à leur premier mariage, qui est un autre événement majeur de leur vie.

Quelque 15 enquêtes de la première phase du programme des Enquêtes démographiques et de santé ont recueilli des données sur la position des décès des parents par rapport au premier mariage. Malheureusement, très peu l’ont fait plus récemment. Des données sur la position des décès parentaux par rapport à la naissance du premier né des répondants pourraient être analysées exactement de la même manière et pourraient être plus représentatives de la mortalité de l’ensemble des parents, dans les populations où nombreux sont ceux qui ne se marient jamais ou lorsque le mariage est davantage considéré comme un processus que comme un événement survenant à une date bien définie.

Comme les hommes et les femmes se marient (et ont leur première naissance) à des âges différents, les réponses des hommes et des femmes interrogés doivent être analysées séparément. Les coefficients d’estimation présentés ici ont été développés en premier lieu pour l’analyse des données fournies par les réponses des femmes (Timæus 1991), mais ils peuvent aussi être utilisés pour l’analyse de données fournies par des hommes, si leur âge moyen au mariage est inférieur à 25 ans. Pour les répondants dont l’âge dépasse l’âge moyen au mariage, les estimations sont robustes vis-à-vis de toute caractéristique de la distribution des âges au mariage autre que sa moyenne.

Devenir orphelin après son premier mariage

La proportion de mères qui sont restées en vie depuis que les répondants sont mariés est étroitement reliée à la probabilité de survivre depuis un âge égal à la somme de l’âge moyen du moment à la naissance des enfants et l’âge moyen au mariage dans les cohortes jusqu’à un âge égal à la somme de l’âge moyen à la naissance des enfants et l’âge actuel des répondants. Les estimations faites à partir des données sur les proportions de répondants devenus orphelins depuis leur mariage mesurent une mortalité plus récente que celles fondées les proportions de répondants devenus orphelins à un moment quelconque de leur vie. De plus, comme les décès parentaux survenus depuis le mariage ont eu lieu alors que les répondants étaient suffisamment âgés pour bien s’en souvenir, ces données sont moins sujettes à erreur de déclaration que celles portant sur la perte des parents en général.

L’âge central des répondants (n) le plus jeune pour lequel on puisse estimer un rapport de survie, _np_b, à partir des données sur les proportions de répondants devenus orphelins depuis leur mariage est 30 ans. Pour les femmes, afin de préserver une relation étroite entre la survie des mères et la fonction de survie des tables de mortalité, cette dernière est mesurée à partir d’un âge de base, b, de 45 ans. Le modèle utilisé pour estimer les mesures des tables de mortalité à partir des proportions de mères survivantes depuis que les répondants sont mariés est donc

$${}_{n-20}p{}_{45}=a(n)+b(n){\overline{M}}^f+c(n)\overline{m}+d(n){}_{5}S{}_{n-5}/{}_{5}S{}_{n-5}^m+e(n){}_{5}S{}_n/{}_{5}S{}_n^m$$

où $$\overline{m}$$ est l’âge moyen au mariage dans les cohortes et $${}_{5}S{}_n^m$$ est la proportion de répondants dans le groupe d’âge n à n + 5 dont la mère était en vie au moment de leur premier mariage.

La seule différence dans l’équation pour l’estimation de la mortalité masculine à partir des proportions de répondants devenus orphelins de père depuis leur mariage tient au fait que les hommes sont généralement plus âgés que les femmes à la naissance de leurs enfants. C’est pourquoi, la fonction de survie est estimée à partir d’un âge plus élevé de 10 ans. Les estimations sont faites à partir de

$${}_{n-20}p{}_{55}=a(n)+b(n){\overline{M}}^m+c(n)\overline{m}+d(n){}_{5}S{}_{n-5}/{}_{5}S{}_{n-5}^m+e(n){}_{5}S{}_n/{}_{5}S{}_n^m$$

où l’âge au mariage continue d’être celui des répondants, qui sont généralement des femmes, pas celui des parents, qui sont cette fois des pères.

Jusqu’à ce que la plupart des répondants soient mariés, la relation entre les survivants de la table de mortalité et les proportions de parents encore en vie est sensible à la forme de la distribution des âges au premier mariage. Des coefficients existent donc pour estimer la survie sur des intervalles d’âge de ₁₀p₄₅ à ₃₀p₄₅ pour les femmes adultes et de ₁₀p₅₅ à ₂₀p₅₅ pour les hommes adultes (voir tableau 8).

Tableau 8 Coefficients pour l’estimation de la mortalité des hommes et des femmes adultes à partir des proportions de répondants devenus orphelins depuis leur premier mariage

n	a(n)	b(n)	c(n)	d(n)	e(n)
Femmes adultes
30	0,5617	0,00836	-0,00261	–1,1231	1,4199
35	0,0476	0,01396	–0,00536	–0,3916	1,1354
40	–0,3715	0,01966	–0,00744	0,5394	0,5286
45	–0,6562	0,02587	–0,00716	1,0208	0,1789
50	–0,8341	0,03045	–0,00561	1,1898	0,0541
Hommes adultes
30	0,0676	0,01588	–0,00633	–1,2070	1,8284
35	–0,5459	0,02273	–0,01083	–0,2509	1,3867
40	–0,8674	0,02622	–0,01135	0,6057	0,7198
Source: Timæus (1991)

 

Devenir orphelin avant son premier mariage

La proportion de femmes dont la mère est vivante au moment de leur mariage est approximativement égale à la probabilité dans la table de mortalité de survivre entre l’âge moyen des mères à la naissance de leurs enfants et cet âge plus l’âge moyen de leurs filles à leur premier mariage. Si les données ne sont pas biaisées par l’effet d’adoption, cette variante de la méthode des proportions d’orphelins a deux caractéristiques intéressantes. Premièrement, elle mesure la mortalité sur un intervalle de temps et un éventail d’âges limités et assez clairement définis. Deuxièmement, elle permet d’étendre rétrospectivement la série temporelle d’estimations de la mortalité fournie par la méthode des proportions d’orphelins jusqu’au moins 30 ou 35 ans avant la collecte des données.

Dans cette variante, un terme d’interaction entre l’âge moyen au mariage et la proportion de parents décédés améliore l’ajustement du modèle. La probabilité de survivre des femmes entre 25 et 45 ans peut être estimée à partir des proportions de répondants devenus orphelins avant leur mariage grâce à l’équation de régression :

$${}_{20}p{}_{25}=a(n)+b(n){\overline{M}}^f+c(n)\overline{m}+d(n){}_{5}S{}_n^m+e(n)\overline{m}{}_{5}S{}_n^m$$

Les coefficients de cette équation pour les différents groupes d’âge définis par n figurent au tableau 9.

Les mêmes considérations s’appliquent à l’estimation de la mortalité adulte masculine à partir des proportions de répondants devenus orphelins de père avant leur mariage. Les estimations de la probabilité de survie entre 35 et 55 ans sont faites grâce à

$${}_{20}p{}_{35}=a(n)+b(n){\overline{M}}^f+c(n)\overline{m}+d(n){}_{5}S{}_n^m+e(n)\overline{m}{}_{5}S{}_n^m$$

Ces coefficients figurent également au tableau 9.

Tableau 9 Coefficients pour l’estimation de la mortalité des hommes et des femmes adultes à partir des proportions de répondants devenus orphelins avant leur premier mariage

n	a(n)	b(n)	c(n)	d(n)	e(n)
Femmes adultes
30	–0,9607	0,00418	0,04466	–0,04291	1,8178
35	–0,9921	0,00429	0,04700	–0,04501	1,8428
40	–1,0129	0,00433	0,04822	-0,04611	1,8607
45	–1,0206	0,00434	0,04861	-0,04648	1,8680
Hommes adultes
30	-1,2719	0,01060	0,04480	–0,04007	1,8383
35	–1,2977	0,01068	0,04652	–0,04124	1,8530
40	–1,3203	0,01070	0,04769	-0,04225	1,8726
45	–1,3232	0,01070	0,04783	-0,04238	1,8753
Source: Timæus (1991)

Les séries finales de coefficients du tableau 9 pour les répondants devenus orphelins de mère et de père avant leur mariage se réfèrent à un groupe d’âge dans lequel à peu près tous les premiers mariages ont été conclus. Ces coefficients peuvent servir à estimer la mortalité à partir des déclarations des répondants de tous les groupes d’âge au-delà de 40 ans. Seule la qualité des déclarations sur les décès des parents et l’âge des répondants eux-mêmes impose un âge limite aux données qui peuvent être utilisées pour estimer la mortalité à partir des proportions de ceux qui sont devenus orphelins avant leur mariage.

Localisation dans le temps des estimations

Comme celles tirées des proportions d’orphelins en général, les estimations à partir des données fournies par les répondants des différentes cohortes, devenus orphelins avant et après le mariage, reflètent la mortalité sur des périodes de temps variables et mal définies. Pour l’avant mariage, les mesures de mortalité se réfèrent à une période qui est le produit de la distribution des intervalles entre le décès des parents et le mariage et de la distribution des intervalles entre le mariage et l’interview. Au degré de précision recherché ici, l’ancienneté de référence des estimations des proportions d’orphelins de mère est égale à l’intervalle moyen entre le décès de la mère et le premier mariage plus l’intervalle moyen du premier mariage à l’interview. Pour les cohortes féminines presque toutes mariées, les âges auxquels les parents sont exposés au risque de décéder sont concentrés entre leur âge moyen à la naissance des enfants et la somme de cet âge et de l’âge moyen de leurs filles à leur premier mariage. L’ancienneté de référence des mesures de mortalité est égale à :

$$T=(N-\overline{m})+{}_{\overline{m}}g{}_{\overline{M}}$$

Le second terme à droite de l’équation 5 peut être estimé par la procédure déjà développée lors de la présentation de la méthode de base (voir l’étape 4). Comme pour les proportions d’orphelins en général, la date de référence des estimations de la mortalité masculine doit prendre en compte les éventuels décès entre la conception et le naissance et est donc calculée en utilisant

$${}_{\overline{m}+0,75}{}^{}g{}_{\overline{M}-0,75}$$.

Pour les répondants devenus orphelins après leur mariage, l’âge auquel les parents débutent leur exposition au risque de décéder est le produit des distributions de leurs âges à la naissance de leurs enfants et des âges de leurs filles au mariage. Pour les groupes d’âge ayant à peu près complété leur nuptialité, on peut estimer l’âge moyen auquel débute l’exposition au risque comme la somme des moyennes de ces deux distributions. L’exposition des parents se prolonge jusqu’au moment de l’interview, $$N-\overline{m}$$ années plus tard. Les anciennetés de référence des mesures de la mortalité sont donc

$$T={}_{N-\overline{m}}g{}_{\overline{M}+\overline{m}}$$

Comme les âges auxquels les pères sont exposés au risque de décès débutent bien après la naissance de leurs filles, cette équation vaut à la fois pour les estimations de la mortalité des hommes et des femmes.

Illustration

La figure 3 illustre les résultats de l’application de la méthode des proportions d’orphelins avant et après leur mariage pour l’estimation de la mortalité adulte aux données recueillies auprès des femmes de 15 à 49 ans dans l’Enquête démographique et de santé (EDS) de l’Egypte en 1988. Ce qui frappe d’abord dans ces résultats, c’est que l’information relative aux répondantes âgées devenus orphelines avant leur premier mariage, recueillie en 1988, permet des estimations de la mortalité adulte qui remonte au début des années 1950. Deuxièmement, les séries supplémentaires d’estimations obtenues en distinguant les femmes orphelines, entre celles qui l’étaient avant leur premier mariage et celles qui le sont devenues depuis, concordent bien avec celles obtenues grâce aux données sur les proportions d’orphelines en général. Ces résultats ne révèlent pas de biais vers le bas résultant d’une sous-déclaration des décès parentaux due à l’effet d’adoption, ni dans les estimations les plus récentes fondées sur les proportions d’orphelins en général, ni dans celles fondées sur les proportions d’orphelins avant leur premier mariage.

 

Image

Figure 3 Trends in the probability of dying between exact ages 30 and 60 estimated from orphanhood, Egypt, 1988 Demographic and Health Survey

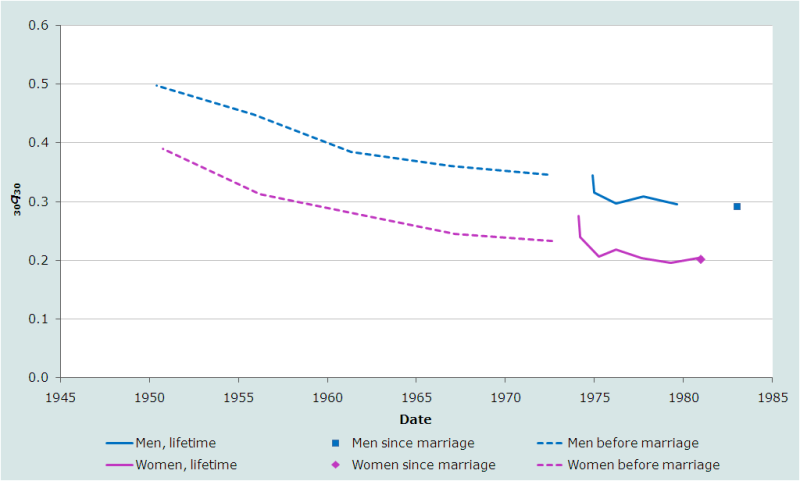
D’après ces résultats, il s’est produit une baisse continue, graduellement ralentie, de la mortalité adulte, en Egypte du début des années 1950 au milieu des années 1980. La probabilité de décéder entre le 30^ème et le 60^ème anniversaire a reculé d’environ 200 pour mille au cours de cette période, pour les hommes comme pour les femmes, à partir d’un niveau très élevé au début des années 1950 jusque vers 200 pour mille pour les femmes et 300 pour mille pour les hommes au début des années 1980. Mêmes ces estimations les plus récentes représentent une mortalité plutôt élevée. L’écart de 100 pour mille entre les probabilités des décéder masculines et féminines n’a guère varié tout au long de la période. Les estimations par les proportions d’orphelins de la mortalité adulte des hommes, en particulier, sont nettement plus élevées que celles fondées sur d’autres sources (UN Population Division 2011).

Questions sur le calendrier des décès parentaux

Une autre extension de la méthode des proportions d’orphelins consiste à demander aux répondants qui ont perdu leurs parents quand est survenu le décès (Chackiel and Orellana 1985). Si les dates de décès des parents sont déclarées avec assez de précision, cela permet à l’analyste de distinguer entre les décès parentaux récents et les plus anciens et d’obtenir des estimations de la mortalité mieux à jour. La meilleure façon d’analyser ces données consiste à utiliser l’information sur les date de décès pour reconstruire la proportion de répondants qui avaient encore leurs parents cinq ans et dix ans plus tôt. De ces coupes transversales successives, on peut tirer des mesures de la survie des parents dans des cohortes synthétiques formellement identiques à celles fournies par les données collectées dans une série d’enquêtes séparées. C’est pourquoi ces méthodes d’analyse sont présentées plus loin, en même temps que l’analyse des proportions d’orphelins tirées d’enquêtes multiples.

Autres lectures et références

La méthode des proportions d’orphelins est présentées dans tous les manuels classiques d’estimation indirecte (Sloggett, Brass, Eldridge et al. 1994; Division de la Population des NU 1984). mais, à l’exception de celui des Nations unies sur l’estimation de la mortalité adulte (UN Population Division 2002), ces manuels s’attachent à l’ancienne variante de la méthode, qui recourt à des facteurs de pondération pour obtenir des indices de tables de mortalité, plutôt qu’à la méthode fondée sur la régression, couramment utilisée aujourd’hui. Les méthodes fondées sur la régression ont été proposées précédemment pour les femmes (Hill and Trussell 1977; Palloni and Heligman 1985), mais elles ont été développées pour les hommes plus récemment par Timæus (1992). Ce dernier article passe aussi en revue des contributions plus anciennes sur le sujet et présente les bases théoriques de la méthode.

Les méthodes d’estimation de la mortalité adulte à partir des proportions de répondants devenus orphelins avant et après leur mariage ont été présentées par Timæus (1991). Les procédures d’estimation de la mortalité féminine dans les populations subissant une épidémie généralisée de VIH ont été développées par Timæus and Nunn (1997).

Luy (2012) a proposé une méthode modifiée des proportions d’orphelins pour étudier les différentiels socioéconomiques de mortalité adulte, dans les pays qui disposent déjà d’une information agrégée précise sur la mortalité adulte. Sa méthode consiste à déterminer la relation entre la proportion de répondants à l’enquête qui déclarent des parents encore en vie et les survivants de la table de mortalité, à partir de statistiques empiriques sur la population concernée, plutôt que de recourir à des modèles démographiques. La méthode de Luy adapte donc le processus d’estimation en fonction du contexte. Rares sont les pays à revenu bas ou moyen qui disposent de données nationales suffisamment précises pour que la démarche puisse s’appliquer, bien que certains aspects puissent se révéler pertinents dans certains circonstances.

Les méthodes qui exploitent les possibilités analytiques supplémentaires, lorsque des questions sur la survie des parents ont été posées dans au moins deux enquêtes successives auprès de la même population, sont présentées ailleurs dans ce manuel.

 

Blacker JGC. 1984. "Experiences in the use of special mortality questions in multi-purpose surveys: the single-round approach," in Data Bases for Mortality Measurement. New York: United Nations, pp. 79-89. https://www.un.org/development/desa/pd/sites/www.un.org.development.desa.pd/files/publications/mortality/mortality_1984_databasesformortalitymeasurements.pdf

Blacker JGC and JM Gapere. 1988. “The indirect measurement of adult mortality in Africa: results and prospects,” in African Population Conference, Dakar, 1988. Liège: International Union for the Scientific Study of Population,Vol. 2:3.2.23–38.

Brass W. 1971. "On the scale of mortality," in Brass, W (ed). Biological Aspects of Demography. London: Taylor and Francis, pp. 69-110.

Brass W. 1975. Methods for Estimating Fertility and Mortality from Limited and Defective Data. Chapel Hill: International Program of Laboratories for Population Statistics.

Brass W. 1985. Advances in Methods for Estimating Fertility and Mortality from Limited and Defective Data. London: London School of Hygiene & Tropical Medicine.

Brass W and EA Bamgboye. 1981. The Time Location of Reports of Survivorship: Estimates for Maternal and Paternal Orphanhood and the Ever-widowed. London: London School of Hygiene & Tropical Medicine.

Brass W and K  Hill. 1973. “Estimating adult mortality from orphanhood,” in International Population Conference, Liège, 1973. Liège: International Union for the Scientific Study of Population, Vol. 3:111–123.

Chackiel J and H Orellana. 1985. “Adult female mortality trends from retrospective questions about maternal orphanhood included in censuses and surveys,” in International Population Conference, Florence, 1985. Liège: International Union for the Scientific Study of Population, Vol. 4:39–51.

Chen W-J and N Walker. 2010. "Fertility of HIV-infected women: insights from Demographic and Health Surveys", Sexually Transmitted Infections 86(Suppl 2):ii22-ii27. doi: https://dx.doi.org/10.1136/sti.2010.043620

De Cock KM, MG Fowler, E Mercier, I de Vincenzi et al. 2000. "Prevention of Mother-to-Child HIV Transmission in Resource-Poor Countries", Journal of the American Medical Association 283(9):1175-1182. doi: https://dx.doi.org/10.1001/jama.283.9.1175

de Walque D. 2007. "Sero-discordant couples in five African countries: implications for prevention strategies", Population and Development Review 33(3):501-523. doi: https://dx.doi.org/10.1111/j.1728-4457.2007.00182.x

Division de la Population des NU. 1984. Manuel X. Techniques indirectes d’estimation démographique. New York : Nations Unies, Département des affaires économiques et sociales internationales, ST/ESA/SER.A/81. https://unstats.un.org/unsd/demographic/standmeth/handbooks/Manuel_X-fr.pdf

Freeman EE and JR Glynn. 2004. "Factors affecting HIV concordancy in married couples in four African cities", AIDS 18(12):1715-1721. doi: https://dx.doi.org/10.1097/01.aids.0000139075.13906.2f

Henry L. 1960. "Mesure indirecte de la mortalité des adultes", Population 15:457-466.

Hill K. 1984. "An evaluation of indirect methods for estimating mortality," in Vallin, J, Pollard John H and L Heligman (eds). Methodologies for the Collection and Analysis of Mortality Data. Liège: Ordina, pp. 145-176.

Hill K and TJ Trussell. 1977. "Further developments in indirect mortality estimation", Population Studies 31(2):313-334. doi: https://dx.doi.org/10.2307/2173920

Kaiser R, R Bunnell, A Hightower, AA Kim et al. 2011. "Factors Associated with HIV Infection in Married or Cohabitating Couples in Kenya: Results from a Nationally Representative Study", PLoS ONE 6(3):e17842. doi: https://dx.doi.org/10.1371%2Fjournal.pone.0017842

Luy M. 2012. "Estimating mortality differences in developed countries from survey information on maternal and paternal orphanhood", Demography 49(2):607-627. doi: https://dx.doi.org/10.1007/s13524-012-0101-4

Mahy M, J Stover, K Kiragu, C Hayashi et al. 2010. "What will it take to achieve virtual elimination of mother-to-child transmission of HIV? An assessment of current progress and future needs", Sexually Transmitted Infections 86(Suppl 2):ii48-ii55. doi: https://dx.doi.org/10.1136/sti.2010.045989

Palloni A and L Heligman. 1985. "Re-estimation of structural parameters to obtain estimates of mortality in developing countries", Population Bulletin of The United Nations 18:10-33. https://www.un.org/development/desa/pd/sites/www.un.org.development.desa.pd/files/files/documents/2020/Jan/un_1986_population_bulletin_18.pdf

Palloni A, M Massagli and J Marcotte. 1984. "Estimating adult mortality with maternal orphanhood data: analysis of sensitivity of the techniques", Population Studies 38(2):255-279. doi: https://dx.doi.org/10.1080/00324728.1984.10410289

Sloggett A, W Brass, SM Eldridge, IM Timæus, P Ward and B Zaba. 1994. Estimation of Demographic Parameters from Census Data. Tokyo, Japan: United Nations Statistical Institute for Asia and the Pacific.

Timæus I. 1986. "An assessment of methods for estimating adult mortality from two sets of data on maternal orphanhood", Demography 23(3):435-450. doi: https://dx.doi.org/10.2307/2061440

Timæus IM. 1991. "Estimation of adult mortality from orphanhood before and since marriage", Population Studies 45(3):455-472. doi: https://dx.doi.org/10.1080/0032472031000145636

Timæus IM. 1992. "Estimation of adult mortality from paternal orphanhood: a reassessment and a new approach", Population Bulletin of The United Nations 33:47-63.https://www.un.org/development/desa/pd/sites/www.un.org.development.desa.pd/files/files/documents/2020/Jan/un_1992_population_bulletin_33.pdf

Timæus IM and AJ Nunn. 1997. "Measurement of adult mortality in populations affected by AIDS: an assessment of the orphanhood method", Health Transition Review 7(Suppl 2):23-43. https://www.jstor.org/stable/40652324

UN Population Division. 2002. Methods for Estimating Adult Mortality. New York: United Nations, Department of Economic and Social Affairs, ESA/P/WP.175. https://www.un.org/development/desa/pd/sites/www.un.org.development.desa.pd/files/files/documents/2020/Jan/un_2002_methodsestimatingadultmort.pdf

UN Population Division. 2011. World Mortality Report 2007. New York: United Nations, Department of Economic and Social Affairs, ST/ESA/SER.A/289. https://www.un.org/development/desa/pd/sites/www.un.org.development.desa.pd/files/files/documents/2020/Jan/un_2007_worldmortalityreport.pdf