Estimation de la mortalité liée à la grossesse à partir de la survie des frères et sœurs
Description de la méthode
L’évaluation et l’utilisation des données de l’histoire complète des frères et sœurs (en anglais : full sibling history, FSH) pour estimer la mortalité adulte dans son ensemble sont décrites par ailleurs. L’histoire complète des frères et sœurs est analogue à une histoire génésique complète : on questionne la personne interrogée (habituellement une femme en âge de procréer) à propos de chacun de ses frères et sœurs nés de la même mère. Pour les frères et sœurs survivants, on demande le sexe et l’âge en années révolues ; pour les frères et sœurs décédés, on enregistre le sexe, l’âge au moment du décès en années révolues et l’année du décès. En ajoutant les données de la femme interrogée, on obtient l’histoire génésique de la mère. Comme l’histoire génésique complète, l’histoire des frères et sœurs permet de situer dans le temps les événements (les décès) et les durées d’exposition au risque, et donc de calculer des taux transversaux de mortalité par âge. Pour estimer la mortalité liée à la grossesse, on recueille des informations supplémentaires sur les décès de sœurs en âge de procréer, en demandant si elles sont mortes alors qu’elles étaient enceintes, lors d’un accouchement ou dans les 42 jours (parfois 2 mois) de la fin d’une grossesse. Ce chapitre est consacré à l’analyse des données sur les sœurs en âge de procréer.
Nous allons aborder ici un important problème touchant les histoires complètes des frères et sœurs. Dans les EDS, l’histoire complète des frères et sœurs consiste à demander à la personne interrogée l’histoire génésique de sa propre mère en s’en excluant elle-même. Par conséquent, on peut se trouver face à plusieurs réponses relatives à la même personne. Par exemple, si deux filles de la même mère sont interrogées dans le même ménage, on obtiendra deux descriptions des autres membres de leur fratrie. Les EDS déterminent les événements et les durées d’exposition uniquement sur la base des frères et sœurs déclarés, sans prendre en compte la durée d’exposition de la femme interrogée elle-même (survivante). De plus, on affecte aux événements et durées d’exposition des frères et sœurs le coefficient de pondération de la personne interrogée, sans tenir compte du nombre de membres survivants de la fratrie susceptibles d’être interrogés. Trussell et Rodriguez (1990) montrent que, s’il n’y a aucune corrélation entre les risques de décès respectifs des frères et sœurs, ce calcul fournit une estimation sans biais de la mortalité générale. Gakidou et King (2006) estiment que la fratrie devrait inclure la personne interrogée et que les données de ses membres devraient en outre être pondérées par leur probabilité d’être déclarés – c’est-à-dire l’inverse du nombre de personnes interrogées potentielles dans la fratrie. Ils pensent également qu’un ajustement serait nécessaire pour prendre en compte les fratries qui ne sont pas déclarées faute de membre survivant. En analysant les FSH de plusieurs EDS, Obermeyer, Rajaratnam, Park et al. (2010) estiment que le fait de ne pas procéder à un ajustement en fonction de la probabilité d’être déclaré peut entraîner pour les indices de mortalité générale une sous-estimation de quelque 20 %. Mais Masquelier (2012) réplique que l’analyse de Obermeyer et al., prenant en compte tous les frères et sœurs survivants et pas seulement ceux qui sont susceptibles d’être interrogés, exagère l’ampleur du biais éventuel. Il recommande d’utiliser le mode de calcul des EDS, pour des raisons qui seront exposées plus loin (voir aussi Analyse de l’histoire des frères et sœurs).
Données requises et hypothèses
Hypothèses importantes
- Il n’y a aucune corrélation entre le risque de décès d’une femme et le nombre de ses frères et sœurs.
- Il n’y a pas d’effet de sélection dû à la migration.
Tabulations nécessaires
- Répartition des femmes par groupes quinquennaux d’âge, d’après le questionnaire-ménage.
- Répartition des décès de sœurs par ancienneté avant l’enquête (habituellement de 0 à 6 ans), par groupes quinquennaux d’âge, et selon que ces sœurs sont décédées alors qu’elles étaient enceintes, ou lors d’un accouchement ou dans les 42 jours (ou 2 mois) de la fin d’une grossesse.
- Nombres de personnes-années d’exposition vécues par les sœurs, selon l’ancienneté du décès et le groupe quinquennal d’âge de la femme interrogée.
- Taux de fécondité par âge et taux global de fécondité de la période considérée avant l’enquête.
Nous supposerons ici que l’on suit l’approche EDS. La construction de tableaux synthétiques à partir des EDS déborde du cadre de ce manuel. Un programme standard de calcul de ces tabulations à partir des données de base existe pour le logiciel CSPro. Il est indispensable de décider, dès le début de l’analyse, de l’horizon temporel à utiliser. La plupart des EDS fournissent les tabulations de base des événements et des durées d’exposition pour les sept années antérieures à l’enquête (de 0 à 6 ans), mais cette période est parfois de cinq ans et parfois de dix ans. Pour choisir une période plutôt qu’une autre, on examine, entre autres, les erreurs d’échantillonnage : avec un petit échantillon et une mortalité adulte assez basse, il vaut mieux opter pour une période rétrospective de dix ans, afin d’éviter une trop grande erreur d’échantillonnage, mais si l’échantillon est grand et la mortalité élevée, on peut se contenter de cinq ans. Cet aspect de la méthode est détaillé dans la section consacrée à l’interprétation des résultats.
Travaux préparatoires et recherches préliminaires
L’évaluation de la qualité des données d’une histoire complète des frères et sœurs et des taux de fécondité par âge récents est décrite par ailleurs. Le seul problème d’évaluation de la qualité des données qui soit propre à l’estimation de la mortalité liée à la grossesse concerne les renseignements sur la part des décès liés à la grossesse parmi les décès de femmes en âge de procréer (en anglais : proportion of deaths of women of reproductive age that are pregnancy-related, PPRD) et sur les proportions de décès liés à la grossesse survenus respectivement pendant la grossesse, lors de l’accouchement et dans les 42 jours (ou 2 mois) de la fin d’une grossesse.
Il n’existe pas de méthode spécifique pour procéder à de telles évaluations. Mais la structure par âge des proportions de décès liés à la grossesse devrait être similaire à celle des taux de fécondité par âge, car l’événement à risque est la naissance. On pense généralement que le risque de décès lié à la grossesse est un peu plus élevé aux extrémités de la tranche d’âge 15-49 ans qu’aux âges intermédiaires, ce qui peut « gonfler » quelque peu les queues de distribution des proportions de décès liés à la grossesse par comparaison avec celles de la distribution des taux de fécondité par âge.
Mise en garde
On pense généralement que l’histoire des frères et sœurs a tendance à sous-estimer la mortalité, en particulier les décès survenus dans un passé éloigné. On ne devrait donc pas essayer d’interpréter les tendances de la mortalité liée à la grossesse sur la base d’une seule série de données. Et ces tentatives menées sur plusieurs séries de données devraient également tenir compte des grands intervalles de confiance qui encadrent les estimations, même pour une période rétrospective de sept ans.
Application de la méthode
Étape 1 : Élaboration des tableaux de données
Comme nous l’avons signalé plus haut, un logiciel facile d’accès permet de construire les tabulations nécessaires relatives aux décès des sœurs, à leurs durées d’exposition au risque et aux décès liés à la grossesse. On a également besoin d’estimations des taux de fécondité par âge. (Si les données concernant les sœurs proviennent d’une EDS, la méthode d’estimation directe des taux de fécondité à partir de ces données est décrite ailleurs dans ce manuel.) Enfin, une estimation de la structure par âge de la population féminine enquêtée est nécessaire.
Définitions de quelques symboles :
- nombre de sœurs déclarées décédées entre les âges x et x+5
- nombre de personnes-années vécues par les sœurs entre les âges x et x+5
- nombre de décès de sœurs liés à la grossesse survenus entre les âges x et x+5
- taux de fécondité des femmes âgées de x à x+5
- nombre de femmes enquêtées âgées de x à x+5.
Des tabulations de chacune des quantités ci-dessus sont nécessaires pour l’application de la méthode.
Étape 2 : Calcul des indices de mortalité
On calcule un taux de mortalité par groupe d’âge en divisant le nombre de décès de sœurs survenus dans ce groupe d’âge par le nombre de personnes-années vécues par celles-ci dans cette tranche d’âge :
(1)
Le taux de mortalité liée à la grossesse (en anglais : pregnancy-related mortality rate, PRMRate), par groupe d’âge, est :
(2)
La part des décès liés à la grossesse parmi l’ensemble des décès de sœurs, par groupe d’âge, est :
(3)
et le rapport de mortalité liée à la grossesse (en anglais : pregnancy-related mortality ratio : PRMRatio), par groupe d’âge, est :
(4)
Étape 3 : Estimation des indices au niveau de la population
On calcule les estimations du taux de mortalité liée à la grossesse et de la proportion de décès liés à la grossesse parmi les décès de femmes en âge de procréer (15-49 ans) en pondérant les indices calculés ci-dessus par les nombres de femmes âgées de 15 à 49 ans des ménages enquêtés. Ainsi,
(5)
et
(6)
et
(7)
Exemple
À titre d’exemple, nous appliquerons la méthode aux données de l’EDS 2004 du Malawi. On a demandé aux femmes interrogées si leurs sœurs étaient en vie, et, pour les sœurs décédées, de situer le décès par rapport à une éventuelle grossesse.
Étape 1 : Élaboration des tableaux de données
Les tabulations de données requises sont présentées dans le tableau 1. Les déclarations de décès de sœurs et de durées d’exposition au risque se réfèrent aux sept années précédant l’enquête.
Tableau 1 Données de base utilisées pour estimer la mortalité liée à la grossesse, EDS Malawi 2004
Groupe | Décès | Durée d’exposition au risque de décès des sœurs | Décès liés à la grossesse | Taux de fécondité par groupe d’âge | Effectifs féminins des ménages |
|---|---|---|---|---|---|
(i) | (ii) | (iii) | (iv) | (v) | |
15-19 | 117 | 27 622 | 8 | 0,162 | 2 570 |
20-24 | 227 | 29 331 | 52 | 0,293 | 3 036 |
25-29 | 299 | 23 763 | 64 | 0,254 | 2 247 |
30-34 | 245 | 17 228 | 50 | 0,222 | 1 516 |
35-39 | 230 | 12 206 | 33 | 0,163 | 1 122 |
40-44 | 177 | 7 892 | 22 | 0,080 | 970 |
45-49 | 82 | 4 574 | 12 | 0,035 | 743 |
Total | 1 376 | 122 616 | 240 | 0,204* | 12 204 |
* Taux global de fécondité : moyenne des taux de fécondité par groupe d’âge pondérée par la structure par âge de la population féminine des ménages. | |||||
Source : EDS Malawi 2004, Tableaux 13.2 (p. 245) et 13.3 (p. 247). | |||||
Étape 2 : Calcul des indices de mortalité
L’application de la méthode aux données du tableau 1 est détaillée dans le tableau 2. La première colonne présente les taux de mortalité par groupe d’âge, calculés en divisant le nombre de décès féminins du groupe d’âge considéré (col. i du tableau 1) par la durée d’exposition au risque de décès des sœurs (col. ii du tableau 1), conformément à l’équation 1. Dans la deuxième colonne figurent les taux de mortalité liée à la grossesse par groupe d’âge, calculés sur le modèle des taux de mortalité générale par groupe d’âge, mais en ne retenant au numérateur que les décès liés à la grossesse (col. iii du tableau 1 ‑ équation 2). La troisième colonne présente, pour chaque groupe d’âge, la part des décès déclarés liés à la grossesse dans l’ensemble des décès féminins déclarés (col. iii/col. i du tableau 1 – équation 3). Dans la quatrième colonne, on trouve les rapports de mortalité liée à la grossesse par groupe d’âge, calculés en divisant le nombre de décès liés à la grossesse (col. iii du tableau 1) par la durée d’exposition au risque de décès des sœurs (col. ii) en multipliant par les taux de fécondité par groupe d’âge (col. iv), et en multipliant par 100 000 (équation 4).
Tableau 2 Taux de mortalité féminine aux âges adultes et taux de mortalité liée à la grossesse, EDS Malawi 2004
Groupe | Taux de mortalité par groupe d’âge | Taux de mortalité liée à la grossesse par groupe d’âge | Part des décès liés à la grossesse | Rapports de mortalité liée à la grossesse par groupe d’âge |
|---|---|---|---|---|
= 1000*(i)/(ii) | = 1000*(iii)/(ii) | = (iii)/(i) | = 100 000*iii /(ii*iv) | |
15-19 | 4,24 | 0,29 | 0,0684 | 178,8 |
20-24 | 7,74 | 1,77 | 0,2291 | 605,1 |
25-29 | 12,58 | 2,69 | 0,2140 | 1 060,3 |
30-34 | 14,22 | 2,90 | 0,2041 | 1 307,3 |
35-39 | 18,84 | 2,70 | 0,1435 | 1 658,6 |
40-44 | 22,43 | 2,79 | 0,1243 | 3 484,5 |
45-49 | 17,93 | 2,62 | 0,1463 | 7 495,8 |
Total* | 11,51 | 1,99 | 0,1681 | 970,7 |
Note : tous les totaux de ce tableau sont pondérés par la structure par âge de la population féminine des ménages enquêtés (voir le texte). | ||||
Il est important de souligner que les résultats de la ligne Total du tableau 2 ne sont pas les simples sommes des chiffres des divers groupes d’âge. La raison en est que la structure par âge des sœurs exposées au risque de décès diffère de celle de la population féminine en âge de procréer. Pour obtenir des totaux corrects au niveau de l’ensemble de la population, il faut re-pondérer les taux et rapports par groupe d’âge du tableau 2 par la structure par âge de la population féminine (col. v du tableau 1) conformément aux équations 5, 6 et 7. De même, le dénominateur de l’équation 7 n’est pas le taux global de fécondité tel qu’on le calcule habituellement (le nombre de naissances divisé par le nombre de femmes âgées de 15 à 49 ans), mais la somme des taux de fécondité par âge pondérée par la structure par âge de la population féminine.
Étape 3 : Estimation des indices au niveau de la population
Le tableau 3 compare la distribution des naissances par groupe quinquennal d’âge (obtenue en multipliant les effectifs féminins des ménages par les taux de fécondité par âge correspondants) avec celle des décès liés à la grossesse (calculée en multipliant les effectifs féminins des ménages par les taux de mortalité liée à la grossesse par âge correspondants).
Tableau 3 Comparaison de la distribution des naissances avec celle des décès liés à la grossesse par groupe d’âge, EDS Malawi 2004
Groupe d’âge | Effectifs féminins des ménages enquêtés | Taux de fécondité par groupe d’âge | Décès liés à la grossesse | Naissances | Proportions de : | |
|---|---|---|---|---|---|---|
décès liés à la grossesse | naissances | |||||
| 15-19 | 2 570 | 162 | 8 | 416 | 0,033 | 0,167 |
| 20-24 | 3 036 | 293 | 52 | 890 | 0,217 | 0,356 |
| 25-29 | 2 247 | 254 | 64 | 571 | 0,267 | 0,228 |
| 30-34 | 1 516 | 222 | 50 | 337 | 0,208 | 0,135 |
| 35-39 | 1 122 | 163 | 33 | 183 | 0,138 | 0,073 |
| 40-44 | 970 | 80 | 22 | 78 | 0,092 | 0,031 |
| 45-49 | 743 | 35 | 12 | 26 | 0,050 | 0,010 |
| Total | 12 204 | 240 | 2 500 | 1,000 | 1,000 | |
Diagnostics, analyse et interprétation
Contrôles et validation
Pour le contrôle et la validation des estimations de la mortalité féminine en général, voir le chapitre de ce manuel consacré à l’analyse des histoires des frères et sœurs. Le contrôle et la validation des données supplémentaires sur la mortalité liée à la grossesse reposent sur des tests de crédibilité. La proportion globale de décès liés à la grossesse parmi les décès de sœurs en âge de procréer est-elle plausible au regard de l’estimation du rapport de mortalité liée à la grossesse ? La structure par âge des décès liés à la grossesse est-elle crédible par rapport à la structure par âge des naissances (les événements à risque) ?
Il n’y a pas de méthode largement reconnue d’évaluation de la plausibilité de la proportion de décès liés à la grossesse. En général, on observe une association positive entre cette proportion et le taux de mortalité liée à la grossesse, mais elle dépend du niveau de la mortalité non liée à la grossesse et ne fournit aucune base utile pour l’évaluation. On estime la plausibilité de la structure par âge des décès liés à la grossesse par comparaison avec la structure par âge des naissances, comme on le voit dans le tableau 3. Dans le cas de l’EDS Malawi 2004, les proportions de décès liés à la grossesse survenus dans les groupes d’âge 15-19 ans et 20-24 ans sont beaucoup plus faibles que les proportions correspondantes de naissances, et c’est l’inverse que l’on observe après 35 ans. Ce dernier phénomène peut s’expliquer par le caractère de plus en plus risqué de la grossesse et de l’accouchement à partir de l’âge de 35 ans, mais aucune explication plausible n’existe pour les importants écarts observés avant l’âge de 25 ans. On a de bonnes raisons de soupçonner que certains décès de sœurs de moins de 25 ans liés à la grossesse n’ont pas été déclarés comme tels.
Interprétation
Pour interpréter les estimations de la mortalité liée à la grossesse à partir des histoires des frères et sœurs, on doit accorder une grande attention aux marges d’erreur d’échantillonnage et aux erreurs habituelles dans les données. L’erreur d’échantillonnage est très importante, comparée à celle qui affecte les estimations de la mortalité en-dessous de 5 ans dans les EDS. La figure 1 met en relation les coefficients de variation (écart-type/valeur estimée) des estimations EDS des taux de mortalité liée à la grossesse avec les nombres de frères et sœurs déclarés. Les coefficients de variation sont supérieurs à 0,08 même pour les très grands échantillons, et supérieurs à 0,10 pour la quasi-totalité des enquêtes.
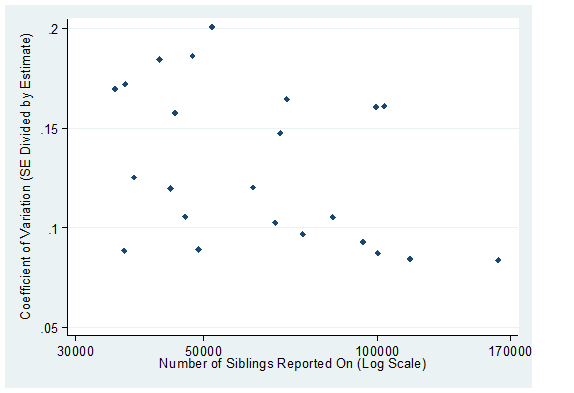
Sources : Stanton, Abderrahim and Hill (2000) pour les estimations antérieures à l’année 2000, et rapports nationaux des EDS pour les années 2004 et suivantes.
Étant donné la grande marge d’incertitude inhérente à l’échantillonnage, l’interprétation de différences observées entre régions infranationales ou entre d’autres sous-groupes tels que les classes d’âge est sujette à caution. Les erreurs courantes des données, en particulier l’omission de certains décès survenus longtemps avant l’enquête, rendent suspecte toute interprétation des tendances décelées. Toutes les conclusions en termes de tendances d’évolution devraient être fondées sur des estimations provenant de deux ou plusieurs enquêtes, portant sur des périodes rétrospectives comparables, et tenir compte de l’erreur d’échantillonnage.
Références
Gakidou E and G King. 2006. "Death by survey: estimating adult mortality without selection bias from sibling survival data", Demography 43(3):569-585. doi: https://dx.doi.org/10.1353/dem.2006.0024
Masquelier B. 2013. “Adult mortality from sibling survival data: A reappraisal of selection biases?”, Demography 50(1):207–228. doi: https://dx.doi.org/10.1007/s13524-012-0149-1
Obermeyer Z, JK Rajaratnam, CH Park, E Gakidou et al. 2010. "Measuring adult mortality using sibling survival: a new analytical method and new results for 44 countries, 1974-2006", PLoS Medicine 7(4):e1000260. doi: https://dx.doi.org/10.1371/journal.pmed.1000260
Stanton C, N Abderrahim and K Hill. 2000. "An assessment of DHS maternal mortality indicators", Studies in Family Planning 31(2):111-123. doi: https://dx.doi.org/10.1111/j.1728-4465.2000.00111.x
Trussell J and G Rodriguez. 1990. "A note on the sisterhood estimator of maternal mortality", Studies in Family Planning 21(6):344-346. doi: https://dx.doi.org/10.2307/1966923
- Printer-friendly version
- Log in to post comments
