Evaluation générale de la qualité des données par âge et sexe
Introduction
« Dans un monde idéal, les données seraient toujours complètes, exactes, actuelles, pertinentes et sans ambigüités. Dans le monde réel, elles sont généralement imparfaites sur l’une ou sur l’ensemble de ces dimensions » (Feeney 2003 : 190). Estimer et évaluer la qualité des données, c’est pour l’essentiel identifier la nature, la direction, l’ampleur et la signification vraisemblable de ces imperfections. L’estimation et l’évaluation de la qualité des données débute juste après que celles-ci ont été élaborées, mais c’est une activité récursive – à chaque étape de l’analyse, l’utilisateur des données démographiques devrait regarder les résultats obtenus d’un œil sceptique, à l’affut d’éventuelles indications d’erreur ou de biais introduits par les données dans les résultats.
Nous exposons ici l’essentiel des recherches qu’un analyste devrait réaliser comme une évidence avant de s’embarquer dans un processus d’analyse démographique. Les principes de base selon lesquels conduire une évaluation et estimation démographiques ont à peine changé dans les cinquante dernières années. C’est pourquoi certains aspects de ce qui est présenté dans cette section sont tirés du Manuel II des Nations Unies (1955), mis à jour et modifié en fonction des nécessités, ainsi que d’un autre guide pour l’évaluation des données de recensement, plus récent, proposé par le U.S. Bureau of the Census (1985). Ce dernier ouvrage est un guide utile et complet pour notre sujet ; les chapitres 4 et 5 sont en particulier fortement recommandés à tous les analystes entreprenant un processus d’estimation et d’évaluation de la qualité des données démographiques.
La section qui suit explique pourquoi il est nécessaire d’évaluer la qualité des statistiques démographiques. Elle offre aussi un survol des principes et des pratiques utilisés.
Nécessité d’apprécier la qualité des statistiques démographiques
Les statistiques de population, comme toutes les autres statistiques démographiques, qu’elles soient obtenues par dénombrement, par exploitation d’un registre ou par d’autres moyens, sont sujettes à erreur. Les erreurs peuvent être larges ou minimes, selon les obstacles à un enregistrement exact dans la zone étudiée, selon les méthodes utilisées pour compiler les données et selon l’efficacité relative avec laquelle ces méthodes sont appliquées. Leur ampleur étant donnée, les erreurs ont une importance plus ou moins grande selon les usages auxquels les données sont destinées. Certaines applications restent valides même si les statistiques sont sujettes à d’assez larges erreurs ; d’autres nécessitent des données plus précises. Quand on traite un problème spécifique, il est important de savoir si les données sont assez exactes pour fournir une réponse d’une précision acceptable.
Pour les estimations de population, l’évaluation de la qualité des statistiques tirées des recensements ou d’enregistrements administratifs sur lesquelles les estimations sont fondées est doublement importante. En premier lieu, une recherche sur la précision des données de base doit précéder tout essai en vue de déterminer la fiabilité des estimations. Les erreurs d’estimation proviennent à la fois d’imprécisions dans les statistiques de base sur la population et d’erreurs dans les hypothèses introduites dans le calcul des estimations (par exemple dans les hypothèses sur les variations de population entre la date des dernières statistiques et la date à laquelle l’estimation s’applique). Il faut prendre en compte les deux sources d’erreur si on veut connaître le degré de confiance à mettre dans les estimations. En second lieu, lorsqu’une recherche sur la précision des données de base révèle des erreurs, dont la direction et l’ampleur peuvent être estimées, il est possible de faire des ajustements compensateurs explicites ou implicites lors de la préparation des estimations de population. Il est fréquent également que des mesures démographiques raisonnablement fiables (par exemple des taux de fécondité) puissent être obtenues, même lorsque les données sous-jacentes ne sont pas fiables sur certains aspects.
Notre propos ici est de décrire les principales méthodes pour apprécier la précision des données de recensement dans leurs aspects les plus couramment utilisés, comme base des estimations de la population actuelle et des projections de la population future. On suppose que les résultats ont été tirés d’au moins un recensement et que l’analyse doit déterminer la précision de celui-ci et des autres données démographiques, sans qu’il soit possible de re-dénombrer l’ensemble de la population ni de recommencer une quelconque partie importante de l’entreprise de recensement.
Il n’est pas possible de voir en détail toute l’information qu’on peut utiliser, dans un pays donné, pour apprécier la qualité de ses données démographiques. Par exemple, des données d’enquête peuvent fournir des estimations des paramètres démographiques utiles pour l’évaluation de la qualité des données tirées d’un recensement. Les exemples présentés ici sont des illustrations des méthodes et les résultats ne doivent pas être pris comme des évaluations définitives de la qualité des données employées.
Les résultats des tests décrits dans le présent manuel sont de divers types. Parfois, un test révèlera seulement que les statistiques ont toutes chances d’être « raisonnablement précises » ou « suspectes » ; si elles sont « suspectes », d’autres recherches seront nécessaires avant qu’un jugement définitif soit porté. D’autres tests ne se contenteront pas d’indiquer qu’il y a des erreurs, mais ils conduiront aussi à estimer la direction et l’ampleur probable de l’erreur. Dans ce dernier cas, il sera souhaitable d’ajuster ou de corriger les statistiques fautives et de réviser les estimations fondées sur elles. La description des procédures à utiliser pour réviser des estimations est toutefois hors du champ du présent manuel.
Une distinction est souvent faite dans les textes démographiques entre les erreurs de couverture (qui résultent de disparités dans le dénombrement entre régions, groupes ethniques, âges, etc. et qui conduisent les données à un défaut de représentativité de l’ensemble statistique qu’elles sont censées décrire) et les erreurs de contenu (résultant d’erreurs du répondant ou de l’agent recenseur, ou de fausses déclarations), mais cette distinction n’est pas très utile pour déterminer les stratégies d’évaluation de la qualité des données. Il est fréquent que les défauts des données ne puissent être attribués exclusivement à l’un ou l’autre type d’erreur. Mais en cherchant à expliquer et à comprendre les erreurs détectées, il peut être utile de considérer où dans le processus de recensement l’erreur peut s’être introduite. Procéder ainsi aide à déterminer les actions appropriées pour corriger les données, si c’est possible. Répétons que la description de ces remèdes est hors du champ du présent manuel.
Documentation de base à rechercher
La conduite d’un recensement est difficile et compliquée – on dit par exemple que le recensement décennal aux Etats-Unis est l’entreprise du gouvernement fédéral la plus grande et la plus complexe en temps de paix (National Research Council 2004). Il en va sans doute de même dans tout autre pays réalisant un recensement. Pour aider dans cette tâche, des normes et procédures recommandées ont été rédigées par la Division statistique des Nations Unies. Nombre des manuels pertinents sont disponibles en ligne : les deux les plus intéressants pour les démographes qui analysent et évaluent la qualité des données de recensement sont les Principes et recommandations concernant les recensements de la population et des logements, (Division statistique de Nations Unies 2008) et le Manuel de vérification des recensements de la population et de l’habitation, (Division statistique des Nations Unies 2010). Le premier propose des conseils pour la logistique de l’organisation d’un recensement, de la planification de l’ensemble de l’opération à la dissémination des résultats ; le second porte sur le traitement des données après les collectes de terrain en vue de la sortie des résultats.
La nature et la qualité des données démographiques disponibles varient largement selon les pays. Les recensements de population sont entrepris avec une fréquence et une précision variables, et les données tirées de l’état civil contiennent des niveaux de détail fortement divergents, et varient énormément en qualité entre pays et à l’intérieur de chacun d’eux. La migration internationale peut être relativement importante ou pas. En conséquence, l’appréciation de la précision des statistiques doit être faite par des méthodes différentes, en fonction de situations différentes ; c’est pourquoi on ne peut pas considérer tous les tests détaillés auxquels peuvent être soumises toutes les sortes concevables de données sur les sujets traités ici. C’est pourquoi aussi les méthodes présentées ici ne peuvent pas toujours être directement applicables à un problème spécifique ; des modifications doivent être introduites pour répondre à des exigences particulières.
Quand c’est possible, l’analyste doit chercher à obtenir autant d’informations pertinentes que possible de la part de l’organisme responsable de la conduite du recensement ou de l’enquête, concernant les pratiques opératoires et les difficultés rencontrées, ainsi que les politiques et les pratiques en matière d’apurement et de correction des données avant leur sortie. Quand une étude post-censitaire a été réalisée, il est nécessaire d’en connaître les résultats.
En plus des sources de données qui peuvent ne pas être dans le domaine public, la qualité des idées qu’on peut se faire sur la nature des données dépendra de la capacité qu’aura l’analyste de mettre à profit autant de matériau que possible susceptible d’être pertinent, pas seulement dans le domaine démographique, mais aussi social, économique, historique et politique. A titre d’exemple (développé plus loin), la baisse spectaculaire des probabilités de survie adulte dans les années 1990, telle qu’indiquée par les données des recensements de 1992 et 2002 au Zimbabwe, peut tenir dans une large mesure aux effets du vih/sida sur la mortalité adulte à cette époque.
Types de tests utilisés
Selon qu’on traite de données de recensement, de statistiques d’état civil ou d’enregistrement des migrations, les mêmes types de tests peuvent être appliqués. Cette similitude vient du fait que les phénomènes démographiques sont liés à la fois entre eux et avec les autres phénomènes sociaux et économiques. Certaines de ces relations sont directes et nécessaires. Par exemple, l’accroissement de population dans un intervalle de temps donné est précisément déterminé par les nombres de naissances, de décès et de mouvements migratoires nets survenant dans cet intervalle. D’autres relations sont moins précises et moins définies. Par exemple, dans certains pays, une dépression économique est susceptible d’entrainer une baisse du taux de natalité – et la prospérité une hausse – mais l’ampleur exacte de la variation du taux de natalité ne peut pas être connue, même à partir d’une connaissance détaillée de la situation économique.
Les types principaux de tests possibles peuvent être résumés ainsi :
- tests de cohérence, fondés sur un ou plusieurs recensements ;
- comparaison des données observées avec une configuration théoriquement attendue, par exemple l’utilisation d’équations d’équilibre et les modèles de projection de population ;
- comparaison des données observées dans un pays avec celles observées ailleurs ;
- comparaison avec des données semblables obtenues pour des usages non démographiques ; et
- vérifications directes (re-dénombrement d’échantillons de la population, etc.).
Le premier type de procédure de contrôle examine la cohérence des données, soit de façon interne (par exemple, la distribution de la population par âge et/ou sexe est-elle conforme aux attentes), ou de façon externe par comparaison avec des données antérieures du même pays. La théorie de la transition démographique nous conduit à penser – typiquement – que les taux de natalité et de mortalité (et donc les taux de croissance de la population) vont baisser de manière cohérente, ordonnée, sans discontinuité majeure. (Une exception est la possibilité qu’au tout début de la transition les taux de natalité s’accroissent). En l’absence de facteurs exogènes clairement identifiables (comme la guerre, la famine ou les épidémies), des écarts à ces régularités suggèrent fortement l’existence de problèmes dans les données.
Les comparaisons du deuxième type ont fortement varié avec les années. Historiquement, les tests les plus courants consistaient à comparer les données avec celles qu’implique la population stable équivalente du pays en question. Avec le début du déclin de la fécondité dans presque tous les pays du monde, il est devenu de plus en plus rare que soient remplies les hypothèses nécessaires pour que des comparaisons de ce type soient pertinentes. Aujourd’hui, les comparaisons cherchent plus souvent à confronter les taux de mortalité des hommes et des femmes et les rapports de masculinité par âge avec ceux qu’on attendrait dans des contextes semblables à ceux de la source de données analysées. En outre, la comparaison avec les résultats de calculs modélisés (par exemple les Perspectives de la population mondiale des Nations Unies ou les projections du Bureau du recensement américain) peut être utilisée pour révéler d’éventuelles incohérences dans les données.
Des « équations d’équilibre » peuvent aussi être utilisées pour tester la cohérence de l’accroissement des populations révélé par deux dénombrements à différentes dates, en utilisant l’accroissement révélé par les statistiques des diverses composantes de la variation de la population – naissances, décès et migrations – pendant le même intervalle. Si toutes les données étaient exactes, les deux mesures de la croissance (ou de la décroissance) seraient équilibrées. Le test ne vaut pas seulement pour la population totale, mais aussi pour les groupes d’âge et sexe et pour d’autres catégories de population identifiables dans les statistiques. En outre, en réarrangeant et en redéfinissant les composantes de cette équation, des appréciations séparées peuvent être portées sur la précision des statistiques de naissances, de décès et de migrations.
Le troisième type de tests repose sur la connaissance préalable d’un pays qu’on peut considérer comme démographiquement semblable au pays étudié. Ce peut être, par exemple, un pays voisin. Mais si cette démarche est adoptée, il faut prendre grand soin de s’assurer que les similitudes entre les deux pays sont suffisamment grandes (pas seulement démographiquement, mais aussi socialement, économiquement, culturellement, etc.) pour autoriser l’extrapolation des données d’un cadre démographique à un autre.
Les deuxième et troisième types de contrôle sont semblables. Les variations démographiques observées dans un autre pays où les conditions sont présumées être semblables peuvent parfois être substituées à une configuration théoriquement attendue. Dans les deux cas, les comparaisons révèleront des différences fortes ou faibles. L’essence du test repose alors sur la réponse à la question : l’écart entre les valeurs observées et attendues peut il être expliqué par des événements historiques ou les conditions actuelles dans le pays dont les données sont testées ? Sinon, il faut en conclure que les données observées sont « suspectes ». Des recherches supplémentaires peuvent apporter une explication de la différence, ou elles peuvent donner des indications claires selon lesquelles les données « suspectes » sont effectivement erronées. Ce genre de méthode est souvent appliqué comme étape préliminaire, pour suggérer les directions dans lesquelles devraient s’engager des tests supplémentaires.
Le quatrième type de test s’appuie sur la disponibilité de statistiques administratives ou d’autres statistiques sociales pouvant éclairer la démographie du pays étudié. Des estimations de la taille de diverses composantes de la population nationale peuvent être tirées de listes électorales, de statistiques d’inscriptions scolaires ou de populations particulières telles que celles des sites du Système de surveillance démographique (SSD), etc. Si de telles estimations diffèrent des données du recensement de la population, la question est de savoir si la différence peut être expliquée de façon satisfaisante. Etant donné la spécificité des données localement disponibles et la nature des comparaisons qui peuvent en être tirées, les tests de ce type ne font pas l’objet d’une discussion ultérieure. Mais il faut prendre soin de ne pas supposer que ces sources alternatives sont inévitablement meilleures que le recensement testé.
Enfin, les vérifications directes impliquent des recherches de terrain, comme une enquête post censitaire. L’avantage d’une vérification directe tient au fait que les individus dénombrés ou les événements individuels enregistrés peuvent être identifiés, de sorte que la cohérence n’est pas seulement vérifiée sur les totaux, mais qu’elle peut aussi porter sur les erreurs spécifiques d’omission ou de double compte. Les contrôles directs sous la forme d’une enquête post censitaire permettent aussi de corriger la population dénombrée pour tenir compte du sous-dénombrement estimé.
Les quatre premiers types de procédure ne donnent qu’une indication de précision relative car les deux séries de données peuvent être sujettes à erreur. Si différentes procédures sont utilisées, ou s’il existe une forte présomption selon laquelle une série de données utilisée dans la comparaison est très précise, la démonstration donne une indication majeure sur les inexactitudes des données testées. Dans de nombreux autres exemples, la comparaison peut seulement révéler qu’au moins une, si ce n’est les deux, séries de données sont erronées.
Les recherches rapportées ci-dessous se concentrent sur le premier et le deuxième types de test. (Les vérifications directes sont présentées brièvement ailleurs, dans la section sur les contrôles de cohérence post censitaires). Chaque fois que ce sera possible, des exemples spécifiques seront inclus. Les données utilisées dans ces exemples seront tirées des données de recensement diffusées par IPUMS (Minnesota Population Center 2015). Mais seule une fraction des données et des connaissances disponibles pour chaque pays a été utilisée pour élaborer ces exemples. De nombreuses données plus pertinentes, dont certaines ne sont publiées nulle part, existent dans ces pays.
Une observation finale avant de décrire les divers tests présentés ici : la plupart des tests (mais pas tous) peuvent être appliqués a des subdivisions géographiques plus réduites, à la réserve près que la migration joue un rôle croissant dans la détermination de la taille et de la forme des populations à des niveaux plus fins de désagrégation. Ici aussi nous nous attendons à trouver des schémas « ordonnés » de variations de population, à la fois au sein de la même subdivision à des périodes intercensitaires successives, et parmi différentes subdivisions lors d’une période donnée. Toute dissemblance devrait pouvoir être expliquée par des différences de condition connues. En pratique, on sait qu’il peut y avoir une diversité considérable dans les taux de variation de la population dans les différentes régions de toute nation. En conséquence, le problème revient à essayer de distinguer entre les variations qu’on peut expliquer dans des termes autres que des erreurs dans les statistiques, et celles où on ne peut pas. Il faut noter que, bien que ces procédures puissent révéler la présence d’erreurs et dans certains cas indiquer leur ordre de grandeur, elles n’offrent pas une base pour des estimations exactes de la taille des erreurs.
Contrôles préliminaires
Avant d’essayer d’évaluer la qualité des données, l’analyste doit :
- Examiner les procédures de dénombrement et l’information sur la qualité de sa réalisation. Ceci inclut de vérifier si une enquête post-censitaire a eu lieu, et si les données doivent être pondérées et, le cas échéant, comment. Quand c’est possible, l’accès doit être cherché aux données non encore corrigées, ou corrigées légèrement, ainsi qu’aux manuels et aux algorithmes utilisés pour corriger les données.
- Vérifier comment les données ont été collationnées dans une forme lisible par une machine. La saisie manuelle a l’inconvénient d’être lente ; la lecture optique – technique utilisée dans de nombreux recensements autour de 2000 et dans les vagues suivantes – est plus rapide, mais elle est sujette à de nombreux autres défauts (par exemple des difficultés à distinguer les 1 des 7 dans de nombreuses écritures), ainsi qu’à des problèmes de lecture des dernières pages des formulaires des recensements, exposées au risque de salissures.
- Comparer les résultats de recensement avec toute autre donnée disponible dans des sources non démographiques se rapportant aux effectifs de la population ou à des parties de celle-ci.
- Comparer la distribution de population révélée par les résultats du recensement avec les caractéristiques connues des subdivisions ; par exemple, la densité de population dans les zones rurales devrait être moindre que dans les zones urbaines.
- Comparer le nombre d’individus et le nombre de ménages (ainsi que le nombre moyen de personnes par ménage et le nombre de ménages d’une seule personne) au niveau national et régional, et par subdivision rurale/urbaine, pour voir si ces résultats sont raisonnables.
Dans le compte du nombre total d’habitants d’un pays, le degré de précision est directement lié à la précision avec laquelle l’ensemble de l’opération de recensement est conduit. Le dénombrement peut être plus ou moins précis que le décompte de certaines composantes de la population, par exemple par groupe d’âge ou d’état matrimonial, mais si toutes les procédures de recensement sont défaillantes et que les caractéristiques de la population n’ont pas été déterminées précisément, il y a peu de chances pour que l’effectif total soit correct. En fait, une des façons d’apprécier la qualité du dénombrement consiste à analyser la précision des données relatives aux différentes caractéristiques de la population. Cette analyse risque de révéler non seulement une classification incorrecte des individus dénombrés mais aussi une tendance à omettre certaines catégories de population. Des efforts particuliers devraient être consacrés à l’appréciation de la complétude des décomptes de recensement dans les zones et les groupes de populations connus pour être difficiles à recenser. Il y a eu par exemple une longue tradition d’omission des très jeunes enfants en Afrique subsaharienne.
Une présentation détaillée des facteurs qui contribuent à la complétude d’un décompte de recensement dépasse les objectifs de ce manuel. On trouvera une discussion approfondie de ces facteurs dans les textes démographiques classiques (par exemple, Shryock and Siegel 1976; UN Population Branch 1955).
Données manquantes et corrigées
Il est improbable que tous les recensés aient répondu aux questions à la fois sur l’âge et le sexe. S’il n’y a pas de données manquantes sur ces variables, c’est presque certainement que les données ont été corrigées. Toute correction n’est pas mauvaise. Cependant, comme la détermination de la fiabilité globale d’un ensemble de données repose, pour une part cruciale, sur la cohérence interne de la structure par âge et sexe de la population, il vaut mieux pouvoir déterminer quelles variables ont été apurées ou corrigées, et pouvoir évaluer la pertinence des règles mises en place à cet effet. Ceci est parfois indiqué sous la forme d’une étiquette attachée aux données, qui peut aussi préciser le type de correction ou d’imputation réalisée pour cette variable. Si c’est le cas, les distributions des données corrigées selon la méthode utilisée pour obtenir les données finales peuvent mettre en lumière les défauts ou les anomalies dans les règles de correction. Quand c’est possible, il est souhaitable d’avoir accès aux données avant correction et apurement (ou très légèrement corrigées/apurées). Malheureusement, peu de pays diffusent des données « étiquetées », encore moins des versions de données avant correction.
Il est également important de connaître la proportion des données d’une variable qui ont fait l’objet de correction ou d’imputation. Si une proportion trop élevée de données ont été déterminées par une procédure de correction ou d’imputation, la distribution qui en résulte reflètera davantage les règles de correction des données que la réalité.
Quand des données sur l’âge manquent pour certaines personnes, ces enregistrements doivent faire l’objet d’une décision. Il n’est pas recommandé de se contenter de les exclure de l’analyse : en procédant ainsi, on réduit la taille absolue de la population et on suppose que la distribution par âge de ceux dont l’âge manque est la même que celle des personnes qui ont déclaré leur âge. Si on pense que c’est le cas, les âges manquants dans les tableaux doivent être répartis proportionnellement à la distribution par âge de la population dont les âges sont connus. Ainsi (en distinguant éventuellement les données par sexe), si nous désignons par Nx la population dénombrée âgée de x et par Nm la population dénombrée dont l’âge manque, nous distribuons ces cas proportionnellement par âge :
Mais s’il y a de fortes raisons de penser que les âges manquants sont regroupés dans une fraction spécifique de la population, la répartition doit être modifiée pour en tenir compte. Par exemple, il peut être souvent raisonnable de penser que les répondants connaissent les âges de leurs enfants en dessous d’un certain âge, disons 20 ans.
Quand il s’agit de répartir des données selon deux dimensions (par exemple l’âge et la région), il convient de suivre la démarche exposée par Arriaga (US Census Bureau 1997). La méthode consiste à mettre à l’échelle de façon itérative les colonnes puis les lignes pour que leurs sommes égalent les totaux marginaux désirés. La convergence est généralement obtenue après quelques itérations. La feuille de calcul jointe suit cette démarche et permet de traiter jusqu’à 20 lignes et 30 colonnes.
Contrôles fondés sur la disponibilité des données d’un seul recensement
Les contrôles fondés sur un seul recensement doivent être réalisés dans tous les cas, même s’il s’avère qu’existent aussi des données tirées de recensements ou d’enquêtes antérieurs. Ces contrôles donnent une première idée sur les données collectées dans le recensement et reposent largement sur une évaluation de la cohérence et de la régularité des données par âge et sexe.
Distributions par âge et sexe
Etant donné le rôle central de l’âge et du sexe dans la détermination des trois composantes des variations démographiques, les recherches sur les distributions de la population par âge et sexe sont fondamentales dans tout processus d’estimation et d’évaluation de la qualité des données. Des recherches de ce type peuvent fournir une information essentielle sur
- la structure par âge et sexe de la population,
- les différences de couverture ou d’omission,
- la précision des âges déclarés ainsi que d’éventuelles attractions par certains âges, et
- si les données ont été corrigées ou non.
Pyramides des âges et autres évaluations graphiques
Nous ne recommandons pas la construction de pyramides des âges comme outil d’évaluation de la qualité des donnes démographiques, même si elles peuvent être utiles pour un certain nombre d’autres applications et si les pyramides animées peuvent être un outil éducatif précieux pour montrer comment les populations se modifient au fil du temps (voir les exemples du Canada ou de l’Allemagne). Historiquement, les pyramides des âges ont été utilisées pour se faire une idée de la structure globale de la population dénombrée par le recensement. Bien que la construction de pyramides rudimentaires soit relativement simple dans Excel, leur bon formatage est laborieux. Plus important : le jugement visuel sur les données est difficile quand les données par âge et sexe sont présentées sous cette forme. Une représentation graphique simple de la population dénombrée par âge et sexe sur le même système d’axes de coordonnées peut donner bien plus facilement la même information (et davantage). La première évaluation des données doit être faite par année d’âge, après quoi on peut passer à l’examen des distributions par groupes quinquennaux.
Identification des âges attractifs
La représentation graphique de la population par année d’âge permet de repérer d’emblée les âges qui attirent des déclarations plus fréquentes que les âges adjacents. Le constat visuel fournit probablement une indication aussi bonne que des mesures comme l’indice de Myers, l’indice de Whipple ou l’indice de régularité sexe-âge des Nations Unies. Ces indices peuvent être utiles pour des fins comparatives mais leurs échelles sont au mieux indicatives et l’information additionnelle qu’ils fournissent par rapport à une simple observation graphique ne justifie pas leur emploi. Le manuel du Bureau du recensement américain conclut de la même façon : « Ces procédures sont utiles comme mesures synthétiques ou pour des fins comparatives, mais elles ne donnent généralement pas d’idée sur les schémas d’erreur dans les données qui ne puisse être tirée d’analyses des données par des méthodes graphiques ou par le calcul de ratios. » (U.S. Bureau of the Census 1985: 140).
L’attraction de certains âges prend généralement – mais pas toujours – la forme de concentrations de la distribution par âge de la population sur des âges terminés pour 0 ou 5. Selon la façon dont la variable âge est recueillie ou calculée au recensement, la concentration peut se faire à d’autres âges. Par exemple, si l’âge au recensement est calculé à partir de la déclaration par le répondant de son mois et de son année de naissance, l’attraction peut être exercée par des années de naissance se terminant en 0 ou 5 (1920, 1925, etc.) et la concentration qui en résultera sur les années d’âge révolu dépendra de la date du recensement. En outre, d’autres formes d’attraction peuvent être difficilement visibles – par exemple celle occasionnée par un enregistrement massif en un point du temps ou par des événements d’importance historique majeure, conduisant à des préférences pour des âges se terminant en 0 ou 5 à cette date.
En l’absence d’événements extérieurs significatifs, on peut s’attendre à une évolution démographique régulière, et donc à une progression harmonieuse des nombres de personnes dénombrées au fil des âges. Dans les pays en développement où la fécondité est restée élevée, on s’attend à ce que la taille de la population décroisse de façon monotone à mesure que l’âge augmente. Si le nombre absolu des naissances a baissé récemment, on s’attend à avoir moins d’enfants aux jeunes âges qu’à des âges un peu plus élevés.
Une limitation à la mise en graphique de la population par âge et sexe est que les distorsions et les erreurs dans les données aux âges avancés risquent d’être cachées par des tailles de population (beaucoup) plus importantes aux jeunes âges. On peut recourir à des ratios ou des taux relatifs peuvent être utilisés pour étudier d’éventuelles distorsions et erreurs aux âges avancés. En l’absence de comparateur, les âges avancés devraient être étudiés séparément.
Rapports d’âge
Alors que l’attraction par certains âges peut être détectée plus facilement par une représentation graphique que par le calcul d’indices, le calcul de rapports d’âge peut fournir des indications utiles concernant d’éventuels sous-dénombrements ou des déplacements entre groupes d’âge. Le rapport d’âge pour un groupe d’âge donné est le ratio du double de la population dans ce groupe d’âge à la somme de la population dans chacun des groupes d’âge adjacents. Algébriquement,
Si on suppose que la variation de population est à peu près linéaire entre les groupes d’âge, le rapport doit être proche de 100. Des écarts à 100, en l’absence de facteurs extérieurs plausibles (par exemple la migration ou des calamités passées ayant affecté des groupes d’âge particuliers), indiquent des erreurs dans les données dues au sous-dénombrement ou à des déplacements.
Une aberration dans les effectifs de population d’un groupe d’âge particulier (qu’elle soit réelle ou qu’elle résulte d’erreurs dans les données) risque de perturber les rapports d’âge dans les groupes d’âge de chaque côté. Si un groupe d’âge est particulièrement peu nombreux, le rapport d’âge sera inférieur à l’unité pour ce groupe d’âge, avec des pointes dans les groupes adjacents.
Rapports de masculinité
Une deuxième catégorie de contrôles résulte du calcul des rapports de masculinité dans la population, à la fois globalement et à chaque âge. Le rapport de masculinité global (sex ratio SR) est le rapport du nombre d’hommes pour 100 femmes dans la population. Ce rapport peut ensuite être décomposé par âge comme suit :
Où nNxi représente la population de sexe i (i= m ou f) dénombrée entre les âges x et x+n.
Comme la mortalité des femmes est généralement inférieure à celle des hommes dans la plupart des populations, le rapport de masculinité doit refléter cet écart des mortalités. Dans les pays développés, le rapport de masculinité à la naissance (nombre de naissances de garçons pour 100 naissances de filles) est typiquement de l’ordre de 105, alors qu’il est plus proche de 100 en Afrique subsaharienne (Garenne 2004). Des valeurs du rapport de masculinité à la naissance, tirées par exemple du sexe de la dernière naissance déclarée au recensement ou à l’état civil, qui s’écartent de cet intervalle indiquent l’existence d’avortements en fonction du sexe, d’infanticides ou de problèmes de déclaration.
En l’absence de migration nette importante, le rapport global reflète la mortalité relative des femmes et des hommes. S’il n’y a pas de raisons spécifiques pour que la mortalité des femmes dépasse celle des hommes (par exemple sélection fœtale liée au sexe, infanticide des petites filles, très forte mortalité maternelle, négligence généralisée à l’égard des femmes telle que discutée par Sen (1992)), on doit s’attendre à ce que le rapport de masculinité global soit légèrement inférieur à 100. Etant donné les différences entre la mortalité des hommes et des femmes, en particulier aux âges avancés, le niveau exact du rapport global dépend fortement de la structure par âge de la population : il est plus faible pour les populations âgées et plus élevé pour les populations jeunes.
Entre la naissance et les âges adultes avancés (autour de 45 ans dans les pays en développement, 60 ans ou plus dans les pays développés) le rapport de masculinité recule lentement, sauf en cas de migration nette significative. Par la suite, le rapport de masculinité tend à chuter rapidement à mesure que la mortalité masculine dépasse largement la mortalité féminine. Un écart à ce schéma est couramment visible dans les pays où existe une forte migration de travail des jeunes adultes différenciée selon le sexe. Si de nombreux jeunes hommes vivent à l’étranger au moment du recensement, il en résultera une forte baisse des rapports de masculinité, suivie par une reprise progressive parmi les hommes plus âgés à mesure que les travailleurs migrants rentrent au pays.
Commentaires pour conclure
Une évaluation complète de la qualité des données recueillies dans un recensement et une enquête doit chercher à expliquer – avec aussi peu d’hypothèses que possible – les caractéristiques observées des données. L’analyste doit être attentif à des problèmes bien connus, souvent rencontrés dans les données de recensement sur l’âge et le sexe – le sous dénombrement des jeunes hommes d’âge actif et la tendance à se vieillir, fréquemment observée dans les pays où existent des formes de protection sociale telles que les pensions de vieillesse. Enfin s’il y eu une immigration significative, il peut être utile d’analyser la population née sur place séparément du reste de la population ; il n’y a pas d’exploitation comparable pour l’émigration, à moins que des données existent par âge, sexe et pays de naissance dans les pays de destination les plus importants.
Exemple
La feuille de calcul jointe présente les données d’un échantillon de 11,35 % du recensement de 2001 au Népal, tel que diffusé par IPUMS (Minnesota Population Center 2015). Les données ont été vraisemblablement corrigées ou apurées, puisqu’il n’y a pas de cas d’âge ou de sexe manquants dans les données. L’analyste doit chercher à déterminer la nature et l’ampleur de ces corrections.
Comme suggéré plus haut, nous commençons par représenter graphiquement la population dénombrée par année d’âge et sexe (Figure 1).
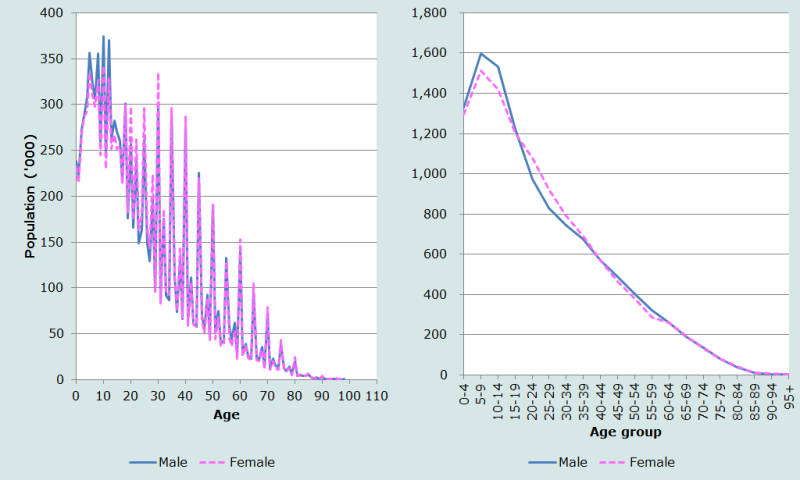
Le graphique de gauche fait apparaître une forte attraction par les âges se terminant par 0 et 5 dans ces données. Par exemple, la population des hommes et femmes dénombrés à 30 ans est plus du triple de celle âgée de 29 ou 31 ans. L’attraction est également visible pour les âges se terminant par 2 et 8. Le phénomène est moins marqué pour la population âgée de moins de 30 ans, même si c’est en partie dû à l’attraction exercée par d’autres âges (8, 12 et 18). La déclaration des âges est manifestement mauvaise dans ces données.
Un fort déficit est également perceptible pour la population dénombrée avant 5 ans, la population dénombrée à 1 an étant à peu près égale aux deux tiers de celle âgée de 5 ans. Il est peu vraisemblable que la fécondité ait baissé autant dans une période aussi brève, aussi la première hypothèse est-elle que des jeunes enfants ont été sous-dénombrés dans ce recensement. Une mauvaise déclaration des âges des enfants – entrainant une surestimation du nombre d’enfants âgés de 5-9 ans – peut aussi avoir contribué au déficit du nombre de très jeunes enfants.
La représentation de la même distribution par âge, mais avec des groupes quinquennaux pour lisser les données (graphique de droite sur la Figure 1), ajoute de nouvelles informations. Le fort déficit de la population âgée de moins de 5 ans apparaît à nouveau, mais la comparaison visuelle de la population âgée de 5-9 ans avec celles de 10-14 ans suggère l’éventualité d’un sous dénombrement des enfants âgés de 5-9 ans aussi. Ceci remet en question l’éventualité d’un large transfert des enfants de 0-4 ans dans le groupe des 5-9 ans. Enfin, les rapports d’âge par groupe quinquennal sont représentés Figure 2.
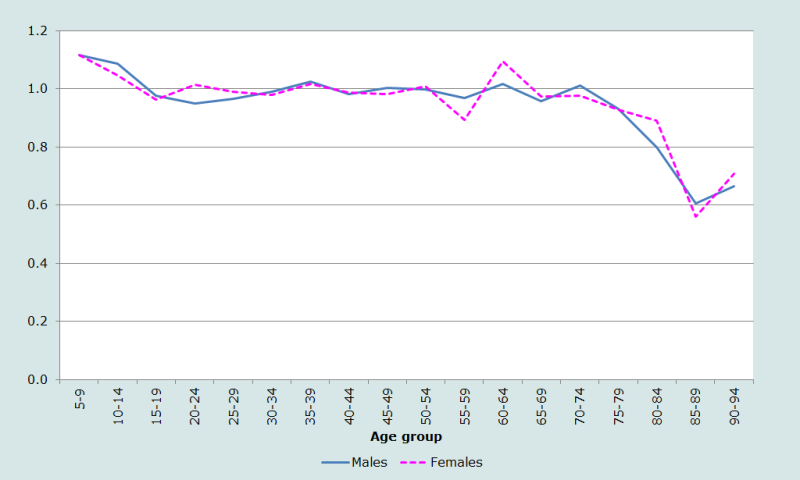
Les rapports d’âge sont généralement proches de l’unité pour les deux sexes, sauf aux plus jeunes âges (indiquant des omissions d’enfants âgés de 0-4 ans et, dans une moindre mesure, un déplacement de ces enfants dans le groupe 5-9 ans). La chute des rapports d’âge aux âges les plus élevés est conforme aux attentes, étant donné l’accroissement rapide de la mortalité à ces âges.
En l’absence d’autres informations, les distributions par âge et sexe ne peuvent pas être analysées plus avant, mais l’analyste peut envisager de comparer la population aux âges pertinents avec des données administratives indiquant les nombres d’enfants inscrits à l’école, ou comparer avec le nombre de naissances déclarées à l’état civil, 5-9 ans et 10-14 ans avant le recensement. Une comparaison peut aussi être faite avec la population estimée âgée de 5-9 ans calculée en appliquant des estimations des taux de fécondité du milieu des années 1990 à la population féminine estimée à la même période.
Une recherche peut aussi porter sur les populations relatives des hommes et des femmes par groupe d’âge. Dans l’ensemble, le rapport de masculinité de la population dénombrée est de 100,5 hommes pour 100 femmes. Il y a un net excès d’hommes dénombrés jusqu’à 20 ans. Entre 20 et 40 ans, il y a plus de femmes que d’hommes. Ceci pourrait être la conséquence d’une émigration de travail (masculine) ou d’un sous-dénombrement différentiel des jeunes hommes adultes. L’analyste doit chercher à expliquer ce phénomène. Il est plausible que l’émigration de travail (masculine) rende compte d’une partie du déficit en hommes ; l’excédent d’hommes dénombrés entre 40 et 60 ans coïncide avec les âges auxquels les hommes peuvent rentrer au pays, mais ceci ne saurait expliquer des rapports de masculinité supérieurs à l’unité. Il se pourrait que les phénomènes sociologiques (avortement lié au sexe du fœtus, infanticide des petites filles) décrits par Sen (1992) pour l’Inde vaillent aussi pour le Népal.
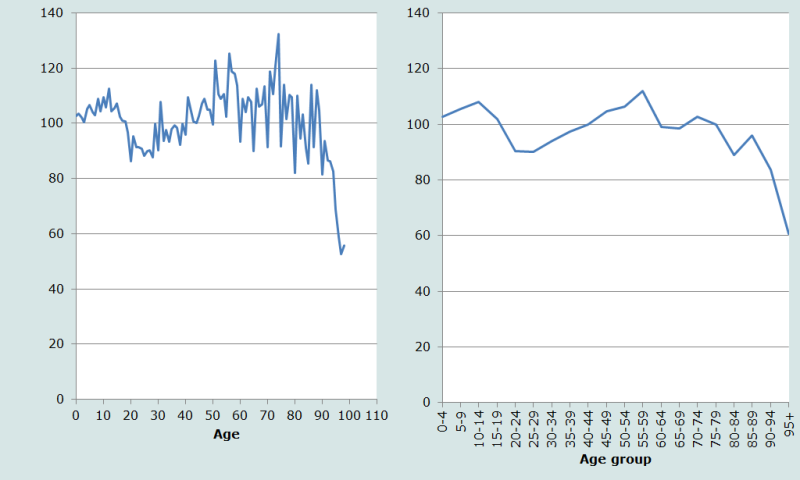
Sur la Figure 3, deux caractéristiques des rapports de masculinité par année d’âge (graphique de gauche) apparaissent. Premièrement, ils sont très erratiques, chutant brutalement à partir de 60 ans aux âges se terminant par 0 et 5. Ceci suggère que l’attraction par les âges ronds joue moins sur les hommes que sur les femmes. Deuxièmement, en plus du déficit en hommes entre 20 et 40 ans déjà décrit, il apparaît aussi un déficit en femmes dans le recensement au-delà de 40 ans, à en juger par le fait que les rapports de masculinité restent supérieurs à (ou proches de) l’unité jusqu’aux âges les plus avancés. Il faudrait une fois de plus s’interroger sur la possibilité d’appliquer l’hypothèse de Sen au Népal.
Les données par groupes quinquennaux (graphique de droite sur la Figure 3) sont plus lisses mais elles confirment néanmoins les analyses ci-dessus.
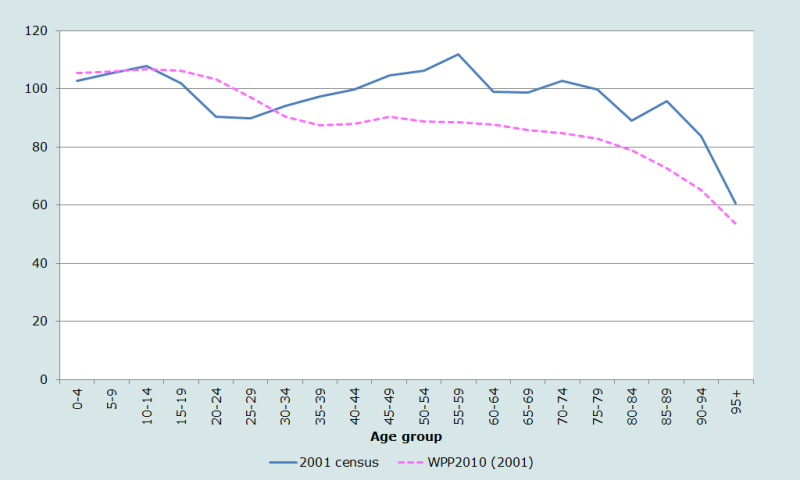
On approfondit ses idées sur la nature et la qualité des données par âge et sexe du recensement de 2001 au Népal en comparant celles-ci aux estimations les plus récentes de la Division de la population des Nations Unies pour le pays en 2001 (Division de la population des Nations Unies 2011). Ces estimations diffèrent largement des données du recensement. La façon la plus efficace d’en rendre compte est de rapporter la population dénombrée (par sexe et âge) à la population estimée par la Division de la population des Nations Unies pour 2001 (Figure 4).
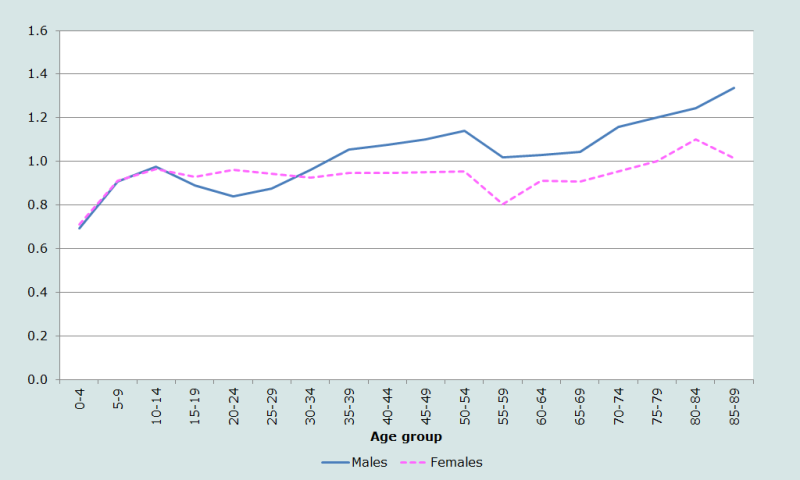
Les estimations des Nations Unies reflétant essentiellement les hypothèses qui les sous tendent, les fortes disparités entre les deux séries d’estimations nécessitent une étude approfondie. Jusqu’à l’âge de 15 ans, les rapports pour les hommes et les femmes suivent à peu près les mêmes tendances. Mais la population des hommes et des femmes dénombrés à 0-4 ans est environ 30 % inférieure à celle estimée par les Nations Unies, alors que celles à 10-14 ans sont très proches à 2 ou 3 % près. Aux âges plus avancés, les schémas des hommes et des femmes divergent fortement, le nombre de femmes entre 15 et 55 ans diffèrant presque constamment de 5 % entre les deux sources.
Par rapport aux projections des Nations Unies, les déclarations des âges apparaissent nettement surestimées aux âges avancés, en particulier chez les hommes.
Il y a aussi des différences notables entre les rapports de masculinité par âge calculés d’après les données du recensement de 2001 et ceux estimés pour 2001 par la Division de la population des Nations Unies (2011) (Figure 5). Des travaux complémentaires seraient nécessaires pour comprendre ce qui peut expliquer les fortes divergences dans la structure démographique du pays.
Contrôles fondés sur plusieurs recensements
En plus des contrôles décrits précédemment, la disponibilité de séries supplémentaires de données tirées de recensements antérieurs (et de systèmes d’enregistrement à l’état civil) rend d’autres recherches possibles.
Il est souvent difficile de déterminer si des irrégularités révélées lors de l’évaluation de la structure par âge et sexe d’une population dans un seul recensement sont principalement dues à des erreurs dans les données ou à de réelles particularités de la structure de population. Quand les résultats de deux recensements ou plus sont disponibles, il devient possible de lever ces incertitudes, même sans recourir à des techniques plus élaborées que celles décrites à la section précédente. Par exemple, si nous avions les statistiques par âge du recensement de 2008 au Cambodge, la possibilité d’expliquer certaines irrégularités dans les données de 1998 comme conséquences de déficits dans les naissances ou de décès au cours de la période Khmer Rouge à la fin des années 1970 s’en trouverait largement éclairée. Si les résultats de 2008 montraient les mêmes particularités dans des groupes de dix ans plus âgés, et non dans les mêmes groupes d’âge qu’en 1998, nous serions en bonne position pour conclure que ces particularités reflètent une réalité plutôt que des erreurs de dénombrement. Quand les données de deux recensements ou plus sont disponibles à intervalle de quelques années, on obtient une information encore plus décisive concernant les erreurs en utilisant des équations d’équilibre ou des calculs analogues à partir des données de certaines cohortes – par exemple en comparant les nombres déclarés à 10-14 ans lors d’un recensement antérieur avec ceux déclarés à 20-24 ans au recensement dix ans plus tard. Quand des données sont disponibles pour une série de trois recensements ou plus, les déclarations successives peuvent être rattachées les unes aux autres de cette façon sur toute la série. Mais pour expliquer les techniques en jeu, le recours aux données de deux recensements suffit à les illustrer.
Une fois de plus, le principe de base dans la comparaison de deux recensements successifs ou plus est que les variations de population se manifestent normalement de manière régulière. Quand on s’éloigne de cette régularité, les écarts doivent pouvoir être expliqués par des événements connus, comme une réduction de l’immigration, une famine ou un autre événement. Les écarts qui ne peuvent pas être expliqués ainsi avertissent de la possibilité d’erreurs, et la présomption d’erreurs est renforcée si les résultats d’autres tests vont dans la même direction. Dans certains pays, il peut être possible d’appliquer ces tests séparément à différents groupes ethniques, si des tableaux par âge et sexe existent pour ces groupes et si des données sont disponibles sur l’immigration et l’émigration de ces groupes (ou si les groupes en question sont peu affectés par la migration internationale).
Les contrôles recourant spécifiquement à plusieurs recensements sont, pour la plupart, fondés sur des méthodes utilisées pour mesurer la mortalité adulte – en d’autres termes, l’évaluation de la cohérence des données est un sous-produit des méthodes d’estimation de la mortalité adulte ; dans certains cas, ce sont même ces méthodes qui sont utilisées directement. Cette section décrit certaines de ces méthodes en s’appuyant sur les données le plus couramment disponibles.
Evaluation des taux de croissance intercensitaires
Le taux de croissance, r, est défini comme
où N(t1) et N(t2) désignent les populations totales aux temps t1 et t2 respectivement.
Si la variation de la population d’un pays tient seulement à l’accroissement naturel, il est peu vraisemblable que le taux moyen annuel de croissance dépasse 3,5 %. Un taux de ce niveau serait le résultat d’un taux de natalité élevé (disons 45 pour 1000 ou plus) et d’un taux de mortalité très bas (disons 10 pour 1000 ou moins). Par ailleurs, en l’absence de forte émigration, la population d’un pays en développement ne décroit que dans des circonstances exceptionnelles. De fait, presque tous les taux d’accroissement naturel observés dans les temps modernes ont été compris dans l’intervalle entre zéro et 3,5 %. Dans quelques pays développés, d’après les Perspectives de la population mondiale 2010, la croissance naturelle est négative. Si dans un pays, le taux de variation de la population approche ou dépasse ces extrêmes sans une immigration ou une émigration massive, la question se pose de savoir si un taux aussi inhabituel a une explication ou si les résultats des recensements sont erronés.
Avec une information, même approximative, sur les conditions de mortalité et de fécondité dans un pays, les limites du taux de croissance vraisemblables peuvent être définies plus précisément.
Si des effectifs de population sont connus grâce à trois recensements ou plus, il devient possible de procéder à une évaluation plus précise en comparant les taux de croissance successifs. Le même principe s’applique à nouveau : on s’attend à ce que la croissance de la population évolue régulièrement, sauf si on peut montrer que des circonstances nouvelles peuvent avoir impliqué un rythme de croissance différent.
Par ailleurs, si les résultats des recensements successifs sous estiment tous la population dans la même proportion, l’estimation de r est correcte. La connaissance de r peut donc donner une indication sur le sous dénombrement relatif des recensements successifs.
Rapports de survie des cohortes
Tout groupe d’âge peut être défini comme cohorte : par exemple, les garçons de moins de 5 ans, les femmes de 50-54 ans ou les personnes de 10-19 ans à la date du recensement. Si un deuxième recensement a lieu exactement dix ans plus tard, les survivants de chaque cohorte auront exactement dix ans de plus au moment du deuxième recensement. Leurs nombres seront réduits par les décès mais ils peuvent être augmentés ou diminués du solde des mouvements d’immigration et d’émigration. En général, la mortalité est le facteur principal ; si le solde migratoire est négligeable, la variation des effectifs peut être utilisée pour calculer un taux de survie analogue à celui des tables de mortalité. Calculé pour une seule cohorte, un tel taux de survie apporte souvent peu d’information sur la précision des statistiques. Un résultat ouvertement absurde révèle clairement une erreur. Par exemple, un accroissement des effectifs d’une cohorte d’un recensement à l’autre est clairement impossible, sauf en cas de forte immigration. Semblablement, même quand la mortalité est très élevée, il est invraisemblable qu’une cohorte âgée initialement de n’importe quel âge entre 5 et 60 ans, soit réduite de moitié dans la décennie qui suit.
On peut porter un jugement plus précis si on compare les taux de survie pour des cohortes de chaque sexe à différents âges. Les taux de survie sont fonction des taux de mortalité par âge et, comme eux, ils suivent généralement plus ou moins le même schéma de variation d’âge en âge, que la mortalité soit basse ou élevée. Le taux de survie s’accroit après les toutes premières années d’enfance et il atteint généralement son maximum vers 10 ans ; il recule ensuite, d’abord très progressivement, puis de plus en plus rapidement à mesure que des âges avancés sont atteints. A la plupart des âges, voire à tous, les femmes ont généralement un taux de survie plus élevé que les hommes du même âge. Si la survie hypothétique calculée pour différentes cohortes s’éloigne significativement de ce schéma, et si aucune explication (telle que la migration) ne peut le justifier, on doit suspecter les statistiques d’imprécision.
Dans quelles conditions de telles comparaisons de cohortes à des recensements successifs peuvent-elles les plus significatives ? Une condition est soit l’absence d’une migration nette importante soit une connaissance détaillée de la composition des migrants par âge et sexe. Une deuxième condition, analogue à la première, est le maintien de frontières immuables. Si les frontières du pays ont changé entre deux recensements, de sorte que des personnes en nombre important ont été ajoutées ou retranchées à la population, la composition par âge et sexe de ces personnes doit être connue pour que l’analyse de cohorte donne une indication précise sur la qualité des statistiques. Une troisième condition est que la population couverte par les deux recensements soit la même. Si, par exemple, l’ensemble de la population est dénombré à un recensement mais que les militaires sont exclus au second, les cohortes d’âge incluant des militaires ne peuvent être comparées sans un ajustement adéquat, à moins que le nombre de militaires soit négligeable. Si les nationaux vivant à l’étranger sont inclus dans un recensement et exclus d’un autre, et si les nombres en jeu sont importants, surtout s’ils sont concentrés sur certains groupes d’âge ou de sexe, ce type d’analyse n’est pas pertinent.
Dans le cas d’un pays où l’immigration est importante, une cohorte peut néanmoins être comparée à deux recensements, même si les données migratoires manquent. Si la population née sur place est réputée n’avoir pas émigré de façon importante, les comparaisons de deux recensements peuvent être limitées à cette population.
Les rapports de survie peuvent être calculés sur n’importe quelle tranche d’âge et n’importe quel intervalle de temps, pourvu qu’on ait des données par année d’âge pour au moins un des deux recensements. Avec le programme décennal de recensements recommandé par les Nations Unies, une tranche de dix ans d’âge est courante.
Méthode
Les rapports de survie des cohortes (CSR) mesurent la proportion des personnes dénombrées aux âges x à x+n au temps t, nNx(t) au premier recensement, qui sont encore survivantes et dénombrées dans un deuxième recensement a années plus tard lorsqu’elles sont âgées de x+a à x+n+a ans au temps t+a, nNx+a(t+a)
Ainsi
Lors de la représentation graphique, ces estimations peuvent être placées au milieu de la période intercensitaire (c'est-à-dire en t+a/2), et au point médian des âges à cette date, x+(a+n)/2 . Une représentation graphique de ces rapports de survie des cohortes permet de se faire facilement une idée rapide de la qualité des données, même si les mises en garde classiques s’appliquent ; une suite étrange de rapports de survie des cohortes indique un défaut des données, sans indiquer si l’erreur provient du premier recensement, du second ou des deux.
Cependant, quand on dispose des données d’un troisième recensement, il se peut que les taux de survie des cohortes tirés des deux premiers recensements apparaissent vraisemblables, alors que ceux tirés du deuxième et du troisième semblent problématiques. Dans ce cas, on est conduit à supposer que le défaut est dans le troisième recensement, pas dans le deuxième.
Enfin, si on dispose d’une table de mortalité appropriée, on peut en tirer un autre ratio en divisant le rapport de survie des cohortes par le taux de survie équivalent dans la table de mortalité. On obtient ainsi un ratio de ratios à chaque âge
Le ratio est égal à l’unité si trois conditions (fortes) sont respectées : qu’il n’y ait pas d’erreur dans le recensement, que la structure par âge de la population dénombrée soit identique à celle décrite par la table de mortalité et que la mortalité soit bien celle indiquée par la table de mortalité. Les écarts à l’unité indiquent soit des erreurs dans les données, soit le choix d’une table de mortalité inappropriée. En outre, dans ces conditions et en l’absence de migration, des ratios inférieurs à l’unité impliquent un sous-dénombrement relatif du second recensement par rapport au premier et vice-versa.
Exemple
Les recensements du Zimbabwe ont été réalisés à dix ans d’écart en 1982, 1992 et 2002 (la date de référence étant fixée au 18 août). Des tableaux de la population dénombrée par âge et sexe sont disponibles dans les Annuaires démographiques disponibles sur le site internet de la Division statistique des Nations Unies (nous avons utilisé le Supplément rétrospectif de 1997 et l’Annuaire 2008). Les données figurent au Tableau 1. Les populations âgées de moins d’un an et de 1-4 ans sont présentées séparément ; elles sont maintenues ainsi pour permettre une meilleure compréhension des changements rapides de la mortalité dans les cinq premières années de vie.
Tableau 1 Population du Zimbabwe par âge et sexe, recensements de 1982, 1992 et 2002
1982 | 1992 | 2002 | ||||||
|---|---|---|---|---|---|---|---|---|
Age | Homme | Femme | Homme | Femme | Homme | Femme | ||
0 | 133 070 | 136 960 | 167 552 | 169 064 | 170 054 | 170 277 | ||
1-4 | 510 260 | 528 390 | 621 411 | 626 664 | 668 008 | 667 730 | ||
5-9 | 612 760 | 619 300 | 821 319 | 832 469 | 764 453 | 769 247 | ||
10-14 | 529 750 | 518 740 | 724 905 | 731 846 | 754 587 | 757 657 | ||
15-19 | 390 160 | 412 610 | 615 728 | 632 510 | 736 686 | 766 890 | ||
20-24 | 290 380 | 364 200 | 466 837 | 523 060 | 564 034 | 658 873 | ||
25-29 | 243 420 | 281 060 | 335 713 | 376 495 | 473 984 | 513 793 | ||
30-34 | 185 400 | 206 760 | 280 066 | 326 299 | 369 836 | 360 291 | ||
35-39 | 147 920 | 170 170 | 229 360 | 259 555 | 235 692 | 268,797 | ||
40-44 | 142 050 | 139 530 | 174 266 | 189 509 | 194 702 | 239 727 | ||
45-49 | 116 490 | 110 390 | 145 437 | 143 441 | 165 437 | 191 168 | ||
50-54 | 111 780 | 90 880 | 133 261 | 147 339 | 128 029 | 173 229 | ||
55-59 | 67 400 | 60 800 | 94 713 | 86 729 | 98 417 | 112 498 | ||
60-64 | 76 850 | 65 260 | 95 510 | 84 213 | 94 447 | 99 420 | ||
65-69 | 38 810 | 38 860 | 51 202 | 50 902 | 64 301 | 67 851 | ||
70-74 | 29 810 | 30 500 | 58 279 | 62 479 | 60 311 | 62 464 | ||
75+ | 39 410 | 46 760 | 52 026 | 68 403 | 71 950 | 92 311 | ||
Inconnu | 7 900 | 6 680 | 15 952 | 18 034 | 19 252 | 25 254 | ||
Total | 3 673 620 | 3 827 850 | 5 083 537 | 5 329 011 | 5 634 180 | 5 997 477 | ||
Comme nous n’avons pas de raison de penser que les personnes ayant omis de déclarer leur âge sont particulièrement concentrées dans certains groupes d’âge, la première étape consiste à répartir le nombre de ces cas (relativement peu nombreux) proportionnellement aux effectifs de population dans chaque groupe d’âge de 0 à 75 ans+. La proportion de personnes d’âge inconnu était de 0,19 % au recensement de 1982 ; elle a doublé au recensement de 2002, atteignant 0,38 %. Les distributions ajustées figurent au Tableau 2.
Tableau 2 Population ajustée du Zimbabwe par âge et sexe, recensements de 1982, 1992 et 2002
1982 | 1992 | 2002 | ||||||
|---|---|---|---|---|---|---|---|---|
Age | Homme | Femme | Homme | Femme | Homme | Femme | ||
0 | 133 357 | 137 199 | 168 079 | 169 638 | 170 637 | 170 997 | ||
1-4 | 511 360 | 529 314 | 623 367 | 628 792 | 670 298 | 670 554 | ||
5-9 | 614 081 | 620 383 | 823 904 | 835 296 | 767 074 | 772 500 | ||
10-14 | 530 892 | 519 647 | 727 187 | 734 331 | 757 174 | 760 861 | ||
15-19 | 391 001 | 413 331 | 617 666 | 634 658 | 739 212 | 770 133 | ||
20-24 | 291 006 | 364 837 | 468 307 | 524 836 | 565 968 | 661 659 | ||
25-29 | 243 945 | 281 551 | 336 770 | 377 773 | 475 609 | 515 966 | ||
30-34 | 185 800 | 207 121 | 280 948 | 327 407 | 371 104 | 361 815 | ||
35-39 | 148 239 | 170 467 | 230 082 | 260 436 | 236 500 | 269 934 | ||
40-44 | 142 356 | 139 774 | 174 815 | 190 152 | 195 370 | 240 741 | ||
45-49 | 116 741 | 110 583 | 145 895 | 143 928 | 166 004 | 191 976 | ||
50-54 | 112 021 | 91 039 | 133 680 | 147 839 | 128 468 | 173 962 | ||
55-59 | 67 545 | 60 906 | 95 011 | 87 023 | 98 754 | 112 974 | ||
60-64 | 77 016 | 65 374 | 95 811 | 84 499 | 94 771 | 99 840 | ||
65-69 | 38 894 | 38 928 | 51 363 | 51 075 | 64 521 | 68 138 | ||
70-74 | 29 874 | 30 553 | 58 462 | 62 691 | 60 518 | 62 728 | ||
75+ | 39 495 | 46 842 | 52 190 | 68 635 | 72 197 | 92 701 | ||
Inconnu |
|
|
|
|
|
|
|
|
Total | 3 673 620 | 3 827 850 | 5 083 537 | 5 329 011 | 5 634 180 | 5 997 477 | ||
En respectant les principes soulignés précédemment, nous étudions d’abord les caractéristiques fondamentales de la population par âge et sexe. En l’absence de données par année d’âge, nous ne pouvons pas examiner cet aspect de la qualité des données. Les distributions de la population du Zimbabwe par âge et sexe sont représentées à la Figure 6.
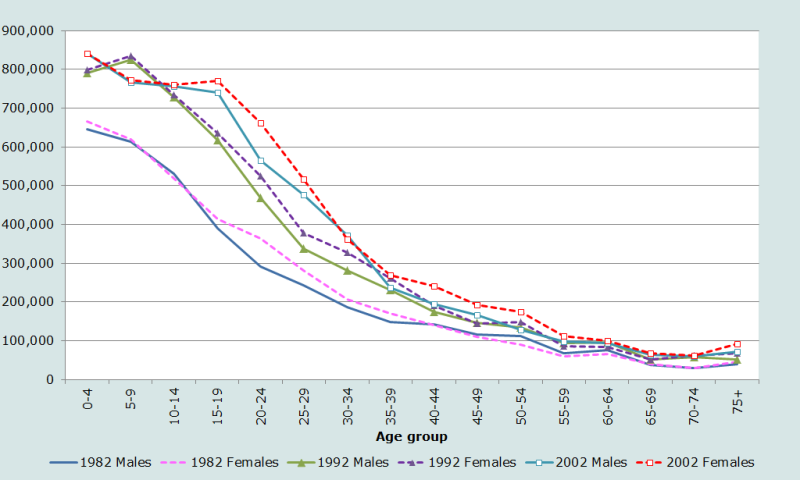
Dans les trois recensements il y a un net excédent de femmes entre 15 et (au moins) 35 ans. C’est presque certainement le résultat de la migration de travail des jeunes hommes vers les pays voisins, en particulier l’Afrique du sud. Il semble y avoir eu un sous dénombrement notable de la population âgée de moins de 5 ans au recensement de 1992 – la population dans ce groupe d’âge est moins nombreuse que celle de 5-9 ans à la même date, à la différence de ce qu’on observe dans les deux recensements adjacents.
Les rapports d’âge et les rapports de masculinité aux trois recensements sont représentés Figure 7.
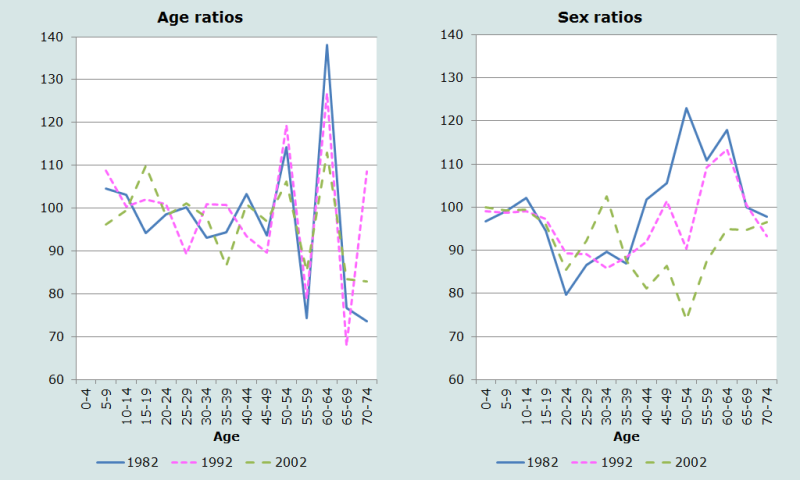
Les rapports d’âge dans le groupe 60-64 ans sont particulièrement élevés dans les trois recensements, et l’excédent de population à ces âges contribue à des très faibles rapports d’âge dans les groupes 55-59 et 65-69 ans. Les rapports de masculinité sont proches de 100 au début et diminuent rapidement après 15 ans dans chaque recensement, probablement du fait de la migration des jeunes hommes. Il est plus préoccupant de constater la hausse des rapports de masculinité entre 35 et 55 ans vers des niveaux largement supérieurs à 100 au recensement de 1982. Ceci reflète presque certainement un sous dénombrement des femmes. Les rapports de masculinité aux âges les plus avancés sont encore très élevés, ce qui reflète probablement une tendance des hommes âgés à se déclarer plus vieux qu’ils ne son en réalité.
L’allure très erratique des rapports d’âge et des rapports de masculinité n’inspire pas une grande confiance dans la qualité des données.
Ensuite, les taux de survie des cohortes sont calculés comme précédemment pour chaque sexe séparément, puisque les schémas et les niveaux de mortalité différent entre hommes et femmes. Comme la population âgée de 0-4 ans en 1992, par exemple, aurait 10-14 ans en 2002, nous supposons que le taux de survie pour cette cohorte s’applique (à peu près) à des personnes âgées de 7½ ans au point médian entre les recensements, en août 1997. Les taux de survie des cohortes ne sont pas estimés pour les très jeunes âges, ni pour l’intervalle ouvert. Les résultats sont représentés graphiquement sur la Figure 8.
Le graphique en haut à gauche représente les taux de survie des cohortes entre les recensements de 1982 et 1992 par sexe ; celui en bas à gauche représente les données équivalentes des recensements de 1992 et 2002. Le sous dénombrement est évident pour les enfants des deux sexes ainsi que pour les femmes jusque vers 20 ans au recensement de 1982 (sauf à imaginer une improbable forte immigration d’enfants entre 1982 et 1992), comme l’indiquent des rapports de survie supérieurs à l’unité.
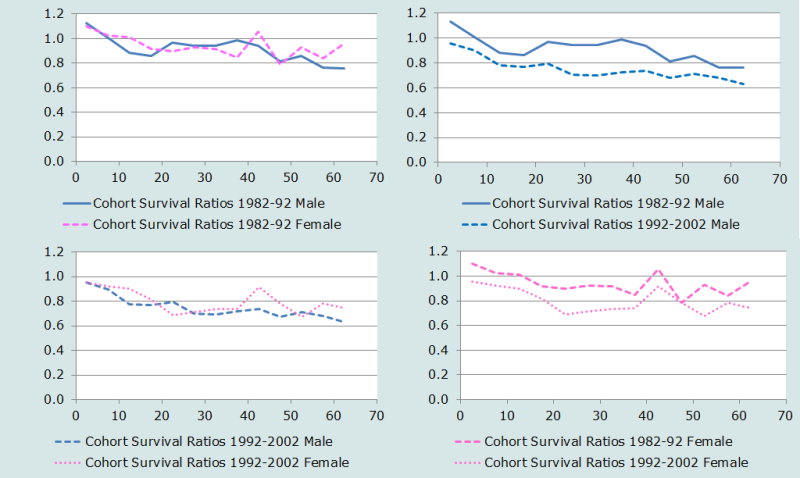
Les deux graphiques de gauche font apparaître (en gros) une décroissance des rapports de survie (une augmentation de la mortalité) au fil des âges, mais les données sont loin d’être cohérentes soit par sexe soit par âge. Il est peu vraisemblable, par exemple, que les rapports de survie des hommes soient plus élevés que ceux des femmes au même âge. Il y a aussi un curieux pic dans les deux périodes intercensitaires des rapports de survie pour les femmes âgées de 40-44 ans au premier recensement et 50-54 ans au suivant. Ceci mériterait approfondissement.
Les deux graphiques de droite représentent les rapports de survie des cohortes au fil du temps, séparément pour les hommes et les femmes. Ils font apparaître une importante augmentation de la mortalité entre les deux périodes de dix ans. La nature erratique des rapports de survie indique que la qualité relative des données est pauvre, mais l’accroissement de la mortalité est presque certainement dû en large part à l’effet du vih/sida parmi les adultes dans la seconde période, conjointement à la dégradation rapide des conditions socio-économiques qui ont prévalu vers le tournant du siècle, ce qui a presque certainement alimenté une forte émigration de jeunes adultes. L’accroissement apparent de la mortalité chez les enfants et les jeunes adultes, visible sur les deux graphiques de droite, est presque certainement dû au sous-dénombrement de cette population en 1982.
Enquêtes post-censitaires
Les enquêtes post-censitaires (EPC) utilisent la logique des techniques de capture-recapture pour estimer la proportion de la population qui n’a pas été dénombrée au moment du recensement. La procédure consiste à retourner dans des zones-échantillons pour ré-administrer un second court questionnaire à tous les ménages qui auraient dû être dénombrés dans cette zone, après quoi les ménages et les individus « capturés » lors de l’enquête sont appariés, chaque fois que possible, avec les ménages et les individus dénombrés lors du recensement. Il doit en résulter une estimation concrète de l’ampleur du sous-dénombrement, qui peut être comparée et opposée à celle tirée, par exemple, d’une projection analytique de la population. Les résultats de l’EPC peuvent ensuite servir à ajuster (« pondérer ») les données du recensement pour compenser les effets du sous-dénombrement.
Une EPC peut donc être très utile. Il y a toutefois deux hypothèses essentielles sous-tendant le recours aux techniques de capture-recapture : un, les probabilités qu’une personne soit atteinte par le recensement et par l’enquête sont indépendantes l’une de l’autre, et deux, il est possible d’identifier le même individu sans ambiguïtés dans les deux sources. La première hypothèse est impossible à tenir dans les populations humaines – certains groupes qui évitent d’être décomptés par un recensement (les immigrés illégaux, par exemple) vont vraisemblablement éviter aussi d’être enquêtés. Dans ce sens, l’EPC ne donne d’information que sur ceux dont on sait qu’ils ont été omis par le recensement, pas sur ceux dont on ne sait pas qu’ils ont été omis. La seconde hypothèse est, elle aussi, difficile à tenir, en particulier dans les zones où la population est très mobile ou si l’intervalle est long entre le recensement et l’EPC.
Les principes et les bonnes pratiques associées à la conduite d’une EPC sont présentés dans un manuel de 2010 (UN Statistics Division 2010).
Quand une EPC a eu lieu, il est bon que l’analyste puisse avoir accès au rapport de l’enquête pour en comprendre les éventuelles faiblesses. La capacité d’une EPC à fournir une information fine sur la qualité des données du recensement est directement liée à la taille de l’EPC et elle est inversement proportionnelle au délai écoulé entre le recensement et l’EPC. Contraint par la durée et le coût de la collecte, l’échantillon d’une EPC est inévitablement beaucoup plus petit qu’un recensement complet. En conséquence, les estimations du sous-dénombrement ne sont possibles qu’à un niveau grossier. Par exemple, au recensement de 2001 en Afrique du sud, les estimations ont été faites par grand groupe d’âge, sexe, groupe de population, province et type géographique de secteur de recensement (urbain, rural, formel, informel). La population est donc supposée sous dénombrée dans la même proportion dans chaque groupe défini par ces cinq caractéristiques. A des niveaux plus fins de décomposition, les estimations du sous-dénombrement risquent de ne pas être fiables.
On peut avoir une idée de l’ampleur des ajustements réalisés et de l’importance du sous-enregistrement à partir d’une évaluation des pondérations fournies avec les données. Si les données brutes tirées d’un recensement ne sont pas ajustées à la suite d’une EPC, les pondérations reflètent le taux de sondage : s’il s’agit d’un échantillon de 10 % des données du recensement, chaque enregistrement sera supposé représentatif de 10 personnes et aura donc un poids de 10. Quand une EPC est prise en compte, le supplément de poids qui s’ajoute au taux de sondage révèle le sous-dénombrement. Analytiquement,
Si un enregistrement a un poids de 11,8 dans un échantillon de 10 % (c’est-à-dire un taux de sondage de 0,1, c’est qu’un ajustement a été effectué pour tenir compte d’un sous-enregistrement de 15,3 % [1-(1/0,1)/11,8).
Quand les données ne sont pas accompagnées d’estimations du sous-dénombrement, l’application de cette dernière formule aux pondérations qui s’attachent aux différents groupes de population permet à l’analyste de retrouver des estimations du sous-dénombrement avec un bon degré de précision.
Références
Division de la population des Nations Unies 1955. Deuxième manuel : Evaluation de la qualité des statistiques de base utilisées pour les estimations de population. New York : Nations Unies, Département des Affaires Economiques et Sociales, ST/SOA/Ser. A/23.
Division statistique des Nations Unies 2010, Manuel de vérification des recensements de la population et de l’habitation. Première Révision. New York : Département des Affaires Economiques et Sociales, ST/ESA/STAT/SER.F/82/Rev.1. http://unstats.un.org/unsd/publication/SeriesF/SeriesF_82Rev1f.pdf
Division statistique des Nations Unies 2008, Principes et recommandations concernant les recensements de la population et des logements. Deuxième révision. New York : Département des Affaires Economiques et Sociales, ST/ESA/STAT/SER.M/67/Rev.2. http://unstats.un.org/unsd/publication/seriesM/seriesm_67Rev2f.pdf
Feeney G. 2003. "Data assessment," in Demeny, P and G McNicoll (eds). Encyclopaedia of Population. Vol. 1. New York: Macmillan Reference USA, pp. 190-193.
Garenne M. 2004. "Sex ratios at birth in populations of Eastern and Southern Africa", Southern African Journal of Demography 9(1):91-96. https://www.jstor.org/stable/20853265
Minnesota Population Center. 2015. Integrated Public Use Microdata Series, International. Version 6.4 [Machine-readable database]. Minneapolis, MN: University of Minnesota. https://doi.org/10.18128/D020.V6.4
National Research Council. 2004. The 2000 Census: Counting under Adversity. Panel to Review the 2000 Census. Citro, Constance F., Daniel L. Cork and Janet L. Norwood (eds), Committee on National Statistics, Division of Behavioural and Social Sciences and Education. Washington DC: National Academies Press.
Sen A. 1992. "Missing women", British Medical Journal 304(6827):587-588. doi: http://dx.doi.org/10.1136/bmj.304.6827.587
Shryock HS and JS Siegel. 1976. The Methods and Materials of Demography (Condensed Edition). San Diego: Academic Press.
UN Population Branch. 1955. Manual II: Methods of Appraisal of Quality of Basic Data for Population Estimates. New York: United Nations, Department of Economic and Social Affairs, ST/SOA/Series A/23. https://www.un.org/development/desa/pd/sites/www.un.org.development.desa.pd/files/files/documents/2020/Jan/un_1955_manual_ii_-_methods_of_appraisal_of_quality_of_basic_data_for_population_estimates_0.pdf
United Nations. 2020. Handbook on Population and Housing Census Editing, Revision 2. New York: United Nations, Department of Economic and Social Affairs, ST/ESA/STAT/SER.F/82/Rev.1.
https://unstats.un.org/unsd/publication/SeriesF/seriesf_82rev2e.pdf
United Nations. 2010. Post-Enumeration Surveys: Operational Guidelines - Technical Report. New York: United Nations, Department of Economic and Social Affairs.
https://unstats.un.org/unsd/demographic/standmeth/handbooks/Manual_PESen.pdf
UN Population Division. 2011. World Population Prospects: The 2010 Revision, Volume I: Comprehensive Tables. New York: United Nations, Department of Economic and Social Affairs, ST/ESA/SER.A/313. https://population.un.org/wpp/Publications/Files/WPP2012_Volume-I_Comprehensive-Tables.pdf
US Bureau of the Census. 1985. Evaluating Censuses of Population and Housing. Statistical Training Document ISP-TR-5. Washington, DC: US Bureau of the Census.
https://www.census.gov/library/working-papers/1985/adrm/rr85-24.html
US Census Bureau. 1997. Population Analysis Spreadsheets for Excel. Washington, DC: US Bureau of the Census. https://www.census.gov/data/software/pas.html
- Printer-friendly version
- Log in to post comments
