La méthode de Preston et Coale

Description de la méthode

La méthode dite de Preston et Coale (Preston, Coale, Trussell et al. 1980) est la seconde des méthodes connues maintenant sous le nom des méthodes de la répartition des décès. Ces méthodes visent à estimer la complétude de la déclaration des décès par rapport à une estimation de la population faite à un instant donné. La méthode de Preston et Coale part de l’observation que le nombre de personnes d’un âge donné vivantes à un instant donné doit être égal au nombre cumulé de décès à venir dans cette cohorte à partir de cet instant. Si la population est stable (c’est-à-dire si la structure par âge est constante, au moins pour les âges adultes, croissante à un taux annuel r, et fermée aux migrations), et si l’enregistrement des décès est complet et précis, alors le nombre de décès d’âge x au cours des t années à venir sera égal au nombre de décès actuel multiplié par $$e^{rt}$$. Il est alors possible d’estimer la population actuelle d’âge y à partir des décès au-delà de l’âge y et du taux de croissance r. Si les décès sont sous-enregistrés, et que l’on peut faire l’hypothèse d’un sous-enregistrement constant c à tous les âges, alors le nombre de décès à venir dans la cohorte sera lui aussi sous-estimé dans la même proportion. Il sera donc possible d’estimer la complétude de l’enregistrement des décès en divisant la somme des décès attendus dans la cohorte par le nombre de décès enregistrés au cours d’une période donnée. Les taux de mortalité peuvent dès lors être calculés en divisant le nombre de décès déclarés dans chaque groupe d’âge par le coefficient c, puis en divisant ces nombres corrigés par une estimation de la population exposée au risque.

Cette méthode est un cas particulier du cas plus général de la méthode de l’extinction des cohortes synthétiques, qui, elle, demande des estimations de la population à deux instants donnés, mais n’exige pas que la population soit stable. Le lecteur est invité à consulter la section correspondante pour avoir plus d’informations sur cette méthode plus générale. La méthode présentée ici est celle que l’on peut utiliser lorsqu’on ne dispose d’estimations de la population qu’à un seul instant donné.

Données nécessaires et hypothèses

Tabulations des données nécessaires

• Nombre de décès de femmes (ou d’hommes) au cours d’une période donnée, répartis par groupe d’âge de 5 ans, et pour le groupe d’âge ouvert A+ (A étant aussi élevé que possible).
• Effectifs de la population féminine (ou masculine) à un instant donné, aussi proche que possible de la période au cours de laquelle les décès sont enregistrés, également répartis par groupe d’âge de 5 ans, et pour le groupe d’âge ouvert A+

Hypothèses importantes

• La population est stable, quoique cette hypothèse puisse être quelque peu relâchée (voir ci-dessous).
• La complétude de l’enregistrement des décès est la même pour tous les âges au-delà d’un âge minimal (en général 15 ans).
• La population est fermée aux migrations, quoique cette hypothèse puisse être relâchée si les migrations nettes sont négligeables par rapport aux taux de mortalité, ou si on dispose d’une estimation suffisamment fiable du nombre de migrants par âge pour permettre de corriger l’équation de la balance de l’accroissement démographique (ce qui est rarement le cas).

Travaux préparatoires et recherches préliminaires

Avant de mettre en œuvre cette méthode, on doit analyser la qualité des données, au moins en ce qui concerne les points suivants:

• structure par âge de la population;
• structure par sexe de la population;
• structure par âge des décès; et
• structure par sexe des décès.

Précautions et mises en garde

Lorsqu’ils appliquent cette méthode, les analystes doivent prendre en considération les points suivants :

• Le processus d’interprétation et d’estimation doit prendre en compte la source des données de mortalité (décès déclarés à l’état civil, décès déclarés par les ménages dans les recensements, ou décès déclarés dans les structures sanitaires), comme cela est expliqué plus loin.
• Le problème des migrations devient plus sérieux quand on applique la méthode à des zones géographiques régionales, et non plus nationales.
• Le choix de l’intervalle d’âges sur lequel on calcule le taux de croissance est important (c’est-à-dire celui qui minimise la différence absolue entre la complétude moyenne et la complétude calculée sur chaque groupe d’âge). Le problème ici est de savoir si la meilleure estimation du taux de croissance à retenir est celle qui est fournie par l’ordonnée à l’origine calculée sur les mêmes données en utilisant la méthode de la méthode de la balance de l’accroissement démographique de Brass. Ceci serait le cas si on pensait que la complétude diminue chez les personnes âgées, comme dans le cas des retraités. Un autre problème est de savoir s’il convient d’exclure les âges en dessous de 30 ou 35 ans du fait de l’impact des migrations que l’on ne peut pas corriger par manque de données.
• Il convient de choisir l’intervalle d’âges à utiliser pour calculer la complétude. En pratique, on devra souvent exclure les jeunes adultes lorsque les migrations sont importantes, et les personnes âgées si les résultats montrent que les décès sont moins bien déclarés à ces âges que chez les jeunes adultes.
• Il faut s’assurer que le module Solveur ;du logiciel Excel; a fonctionné correctement, c’est-à-dire qu’il fournit des résultats réalistes. Il peut arriver que ce logiciel produise une solution qui est manifestement trop faible. Dans un tel cas, il sera préférable d’ajuster d’abord le coefficient ;delta à la main dans une direction appropriée, puis d’appliquer le module Solveur; à cette nouvelle valeur.
• Il faut également s’assurer que l’estimation de l’espérance de vie dans le groupe d’âge ouvert est réaliste. Il est fréquent que les données concernant les personnes âgées soient déficientes et soient sujettes à des erreurs particulières. Dans ce cas, les estimations de l’espérance de vie calculées d’après ces données erronées sont irréalistes (trop élevées le plus souvent).
• Si la complétude de l’enregistrement des décès tombe en dessous de 60%, on invite à la prudence dans l’application de la méthode, car la marge d’erreur de cette estimation peut être considérable.

Application de la méthode

La méthode s’applique en suivant les étapes détaillées ci-dessous :

Etape 1: Calculer le taux de croissance initial

Au départ, le taux de croissance peut se calculer soit à partir de la croissance de la population au-dessus d’un âge donné (choisi pour ajuster au mieux l’hypothèse de stabilité de la population) au cours d’une période, soit à partir de l’estimation fournie par la méthode de la balance de l’accroissement démographique de Brass. Dans le premier cas, si l’on dispose de la population à deux instants donnés (t₁ et t₂), le taux de croissance se calcule comme suit :

$$r=\frac{\ln \left({\text{}}_{\infty }{N}_x(t_2)/{\text{}}_{\infty }{N}_x(t_1)\right)}{t_2-t_1}$$

où $${}_{\infty }{N}_x(t)$$ est la population âgée de x années et plus au temps t.

Etape 2: Estimer l’espérance de vie à l’âge A et dans les groupes d’âge quinquennaux en remontant jusqu’à 65 ans

Ce calcul peut se faire de plusieurs manières:

1. Utiliser des estimations provenant de sources indépendantes si elles sont fiables. On pourra utiliser des estimations faites au cours de recherches antérieures, ou des projections de population telles que les « Perspectives de la Population Mondiale » réalisées par les Nations Unies (UN Population Division 2011).
2. Utiliser l’estimation fournie par la méthode de la balance de l’accroissement démographique de Brass, appliquée aux mêmes données. Le classeur Excel qui met en œuvre cette méthode produit de telles estimations parmi ses différents résultats.
3. Utiliser une table-type de mortalité. On peut par exemple partir du rapport entre les décès de 10 à 39 ans (âge au dernier anniversaire) aux décès de 40 à 59 ans (âge au dernier anniversaire), noté ₃₀D₁₀/₂₀D₄₀ , pour trouver le niveau correspondant de la table de mortalité dans le modèle Ouest de Princeton, et en déduire ainsi les espérances de vie. Ce mode de calcul est inclus dans le classeur Excel de cette méthode. Mais comme la table-type du modèle Ouest ne reflète pas la mortalité due au VIH/sida, cette approche n’est pas appropriée pour les pays qui ont un nombre élevé de décès par sida.
4. Travailler par approximations successives pour trouver l’espérance de vie qui convient. On part d’une valeur raisonnable, par exemple à partir d’une table-type du modèle Ouest (quoique cette stratégie puisse ne pas marcher dans les pays fortement affectés par le sida), ou de sources indépendantes. On fait une première estimation de la complétude selon la méthode exposée ci-dessous, puis on copie et colle ces valeurs dans la feuille de calcul Méthode du même classeur Excel, et on effectue une nouvelle estimation de la complétude. On répétera la procédure plusieurs fois si nécessaire, jusqu’à ce que l’on obtienne une estimation stable de l’espérance de vie. Mais si on a de bonnes raisons de soupçonner que la mortalité reste sous-estimée aux âges élevés, même après la correction pour tenir compte de la sous-déclaration des décès (par exemple lorsque les âges élevés sont exagérés, ou que la complétude est beaucoup plus faible aux âges élevés), cette approche risque de surestimer les espérances de vie, et donc de surestimer le niveau général de complétude de l’enregistrement des décès.

Etape 3: Estimer le nombre de personnes qui atteignent l’âge x, et le groupe d’âge de x à x+4, à partir du nombre de décès déclarés

Le nombre de personnes qui atteignent l’âge x (leur anniversaire) au cours de la période concernée (celle où les décès sont déclarés) s’estime à partir des décès déclarés comme suit :

$${\widehat{N}}_x={\widehat{N}}_{x+5}\exp (5r)+{\text{}}_5{D}_x\exp (2,5r)$$

et

$${\widehat{N}}_A={\text{}}_{\infty }{D}_A\left(\exp \left(r\times e_A\right)-{\left(r\times e_A\right)}^2/6\right)$$

où A représente l’âge au début de l’intervalle ouvert, r est le taux annuel de croissance de la population, et e_A est l’espérance de vie à l’âge A.

Le nombre de personnes qui atteignent le groupe d’âge quinquennal entre x et x+4 (âge au dernier anniversaire) au cours de la période concernée se calcule à partir des effectifs quinquennaux comme suit :

$${}_5{\widehat{N}}_x=2,5({\widehat{N}}_x+{\widehat{N}}_{x+5}).$$

Etape 4: Estimation du nombre de personnes dans le groupe d’âge x à x+4 au dernier anniversaire au cours de la période concernée, où les décès sont enregistrés, à partir d’un recensement de population

Les effectifs de la population du groupe d’âge x à x+4 (âge au dernier anniversaire) au cours de la période concernée (celle où les décès sont enregistrés) sont calculés à partir d’un recensement de population, en multipliant les effectifs de chaque groupe d’âge par la durée de la période concernée (exprimée en années).

Etape 5: Calcul des rapports entre les estimations de la population âgée de x à x+4 au dernier anniversaire et celles de la population âgée de x à A-1 au dernier anniversaire, mesurées d’après les décès enregistrés et d’après le recensement de population.

On calcule les rapports des deux ensembles d’effectifs par âge : ceux provenant des décès déclarés et ceux provenant du recensement de population. On  calcule d’abord directement les rapports des groupes d’âge quinquennaux. On calcule ensuite les rapports des effectifs dans les groupes d’âge cumulés entre l’âge x et l’âge A du début de l’intervalle ouvert et les effectifs cumulés des personnes qui atteignent le groupe d’âge entre x et A-1 au cours de la période concernée, qui se calcule comme la somme des effectifs dans les groupes d’âges quinquennaux situés entre x et A-5. En formule, cela donne :

$${}_{A-x}{\widehat{N}}_x={\displaystyle \sum _{a=x,5}^{A-5}{}_5{\widehat{N}}_x}$$

Etape 6: Estimation de la complétude de la déclaration de décès

Pour déterminer le niveau de complétude de la déclaration des décès, on doit d’abord décider si le choix initial du taux de croissance est correct. L’interprétation des graphiques des rapports est discutée en détail ci-dessous. En résumé, un taux de croissance correct se repère graphiquement comme celui qui produit un ensemble de rapports par âge de même niveau, c’est-à-dire horizontal. La feuille de calcul Méthode est faite pour réaliser ce calcul à l’aide du module Solveur (Données / Solveur / Résoudre) : elle permet de trouver le taux de croissance qui minimise l’écart absolu par rapport à la moyenne des rapports sur un intervalle d’âge spécifié par l’utilisateur.

Si la valeur initiale choisie pour le taux de croissance produit une série de rapports de même niveau pour les groupes d’âges des jeunes adultes, mais qu’elle donne une courbure vers le bas aux âges élevés, cette situation peut indiquer une baisse de la complétude aux âges élevés (ce qui peut être le cas si, par exemple, les personnes qui prennent leur retraite migrent des zones urbaines vers les zones rurales où la complétude de l’enregistrement est plus faible). Dans de tels cas, il est important de ne pas prendre un taux de croissance qui produirait un ensemble de rapports de niveau très horizontal, mais de garder plutôt le taux de croissance choisi initialement.

Si l’utilisateur cherche à ajuster par itération à la fois le taux de croissance et l’espérance de vie, il faudra copier et coller les valeurs trouvées dans la feuille de calcul Espérances de vie dans la feuille de calcul Méthode, et calculer un nouveau taux de croissance. Il faudra alors répéter deux ou trois fois l’opération, jusqu’à ce que l’estimation de l’espérance de vie devienne stable.

Enfin, il faudra décider quel intervalle d’âge utiliser pour l’estimation de la complétude à partir de l’analyse graphique des rapports par âge. Si l’on observe une courbure significative vers le haut aux âges élevés, on est probablement en présence d’une surestimation de l’âge, surtout pour les décès. Il conviendra alors d’essayer d’identifier cet âge en dessous duquel l’exagération de l’âge n’est plus importante, et de le prendre pour début de l’intervalle ouvert. Si la complétude baisse en dessous de l’âge de 35 ans, il pourra s’agir d’émigrations nettes qui n’ont pas été prises en compte. Dans ce cas, il conviendra d’exclure ce groupe d’âge pour recalculer le taux de croissance et la complétude.

La complétude se calcule à partir des rapports par groupe d’âge. Afin de produire des estimations robustes, on propose de la calculer comme la somme pondérée suivante : 50% de la médiane, plus 25% de premier et du dernier quartile de la distribution de ces rapports (les quartiles sont définis comme les percentiles situés à 25% et 75% de la distribution).

Cependant, comme le calcul de la complétude se fait en prenant pour hypothèse que le recensement de population est réalisé au milieu de la période au cours de laquelle les décès sont enregistrés, il est souhaitable d’effectuer une correction pour tenir compte de la croissance de la population entre l’instant précis du recensement (t_c) et l’instant correspondant au milieu de la période d’enregistrement des décès (t_m). Pour ce faire, on multiplie l’estimation de la complétude par le rapport des deux populations au temps t_c  et t_m. En faisant l’hypothèse que la croissance est exponentielle au cours de l’intervalle, à un taux annuel constant a, cela donne : $$\text{}\exp \left(a\left(t_c-t_m\right)\right)$$ où t_c est l’instant du recensement, et t_m est le milieu de la période au cours de laquelle les décès sont enregistrés.

Etape 7: Estimation des taux de mortalité après correction du sous-enregistrement des décès

Afin de calculer les taux de mortalité corrigés, on doit d’abord estimer la population par groupes d’âge quinquennaux au milieu de la période au cours de laquelle les décès sont enregistrés, en multipliant les effectifs du recensement par : $$\text{}\exp (-a(t_c-t_m))$$.

Ensuite, il faut corriger les nombres de décès déclarés en les divisant par l’estimation de la complétude, c.

Les personne-années vécues au risque sont calculées en multipliant la population moyenne au temps t_m par la durée de la période au cours de laquelle les décès sont déclarés, t.

Les taux de mortalité corrigés du sous-enregistrement des décès sont alors calculés comme suit :

$${\text{}}_5{m}_x=\frac{{}_5{D}_x/c}{t\times {\text{}}_5{N}_x\exp \left(-a\left(t_c-t_m\right)\right)}\text{}\text{}.$$

Comme à la fois le numérateur (à travers l’estimation de c), et le dénominateur sont multipliés par le même coefficient : $$\exp \left(-a\left(t_c-t_m\right)\right)$$ , omettre ce coefficient haut et bas (dans les étapes 6 et 7) fournirait les mêmes taux de mortalité. Mais l’estimation de la complétude serait biaisée, et équivalente à ce qu’elle serait si la taille de la population au temps t_m était la même que celle mesurée au temps t_c.

Etape 8: Lissage en utilisant un système logit de tables-type de mortalité

Lorsque les taux de mortalité par âge sont erratiques, ils doivent être lissés. Ceci peut se faire en ajustant un modèle logit (modèle relationnel de Brass) à un ensemble de taux de mortalité tirés d’une table-type, choisie en considérant qu’elle a approximativement le même schéma par âge que celle de la table de mortalité de la population étudiée.

Le classeur Excel associé à la méthode contient une feuille de calcul qui permet de produire un ensemble de taux de mortalité lissés par un système relationnel logit, qui ajuste les taux corrigés de mortalité calculés selon la méthode décrite ci-dessus. L’utilisateur a le choix entre un standard de la famille du modèle Général des tables-type des Nations Unies, ou d’une des quatre familles des modèles régionaux des tables-type de Princeton. On peut aussi utiliser arbitrairement une autre table choisie comme standard lorsqu’on a de bonnes raisons de penser qu’elle ressemble plus au schéma par âge de la mortalité de la population étudiée.

Afin de réaliser le lissage, les quotients de mortalité des personnes entre les âges x et x+5, notés  ₅q_x, sont calculés à partir des taux de mortalité corrigés, selon la formule :

$${\text{}}_5{q}_x=\frac{5{\text{}}_5{m}_x}{1+2,5{\text{}}_5{m}_x}\text{}.$$

Ces quotients permettent de calculer les survivants à chaque âge dans la table de mortalité, qui commence avec une racine  l₅ = 1, en utilisant de proche en proche la formule suivante:

$$\text{}{l}_{x+5}=l_x\left(1-{\text{}}_5{q}_x\right).$$

Les coefficients α et β du modèle relationnel logit sont déterminés par la régression linéaire suivante :

$$\text{}{\gamma }_x=\alpha +\beta {\gamma }_x^s\text{}$$

où

$${\gamma }_x=0,5\ln \left(\frac{1-l_x}{l_x}\right)$$

et l’exposant s désigne les valeurs de la table type.

On peut alors en déduire la table de mortalité, corrigée et lissée, à partir de la table-type choisie et des coefficients α and β comme suit:

$${\gamma }_x^{fitted}=\alpha +\beta {\gamma }_x^s$$

et

$$l_x^{fitted}=\frac{1}{\exp \left(1+2{\gamma }_x^{fitted}\right)}.$$

La série des survivants permet de calculer les taux de mortalité selon les formules suivantes:

$${}_5{m}_x^{fitted}=\frac{l_x^{fitted}-l_{x+5}^{fitted}}{T_x-T_{x+5}}$$

et

$${}_{\infty }{m}_x^{fitted}=\frac{l_x^{fitted}}{T_x}$$

où

$$T_x={\displaystyle \sum _{x=x,5}^{\omega }\frac{5}{2}\left(l_x^{fitted}+l_{x+5}^{fitted}\right)}$$

c’est-à-dire :

$$T_x=T_{x+5}+\frac{5}{2}\left(l_x^{fitted}+l_{x+5}^{fitted}\right)$$

et ω est l’âge au-delà duquel il ne reste plus de survivant dans la table de mortalité.

On calcule alors l’espérance de vie comme suit:

$$e_x=\frac{T_x}{l_x}.$$

Dans le cas où l’on souhaite estimer l’espérance de vie aux âges élevés par itération, ces valeurs peuvent être utilisées pour ré-estimer la complétude.

Exemple

Cet exemple utilise les données de la population féminine du Salvador au recensement de 1961, et les décès de l’état civil de l’année 1961. Le classeur Excel ‘PnC_El_Salvador’ est basé sur ces données. La date de référence du recensement de 1961 est la nuit du 5 au 6 mai, et c’est ainsi que la date du recensement est entrée (06/05/1961) dans la feuille de calcul intitulée ‘Introduction’.

Etape 1: Choix du taux de croissance initial

Le taux de croissance estimé à partir de la population âgée de 10 ans et plus aux recensements de 1950, 1961 et 1971 est de 2,8%, et c’est cette valeur qui figure dans le Manuel X. Le taux de croissance calculé en appliquant la Méthode de Brass de la balance de l’accroissement démographique à ces données est de 3,1%, qui est très proche de l’estimation que l’on peut faire à partir de la population moyenne en 1955 et 1965 qui figure dans International Data Base of the US Census Bureau, et qui se calcule comme suit :

$$r=\frac{\ln \left(3017852/\text{}2221139\right)}{1965-1955}=0,0307.$$

Etape 2: Estimer l’espérance de vie à l’âge A et pour les intervalles d’âges de 5 ans en 5 ans, jusqu’à 65 ans

Ces estimations proviennent des données, après leur avoir appliqué la Méthode de Brass de la balance de l’accroissement démographique, comme cela est indiqué dans la colonne 2 du tableau 1.

Les rapports du nombre de décès déclarés dans le groupe d’âge 10-39 ans, âge au dernier anniversaire (1706 décès), au nombre de décès dans le groupe d’âge 40-59 ans, (1467 décès) est de :

$$\frac{1706}{1467}=1,16$$

. Les espérances de vie par âge qui correspondent à ce niveau de mortalité dans la table-type du modèle Ouest (que l’on trouve dans la feuille du calcul Espérances de vie du classeur Excel), se calculent par interpolation entre les deux niveaux encadrant, comme indiqué dans la colonne 3 du tableau 1. Par exemple, pour l’âge de 65 ans :

$$e_{65}=9,50+\frac{1,171-1,16}{1,171-1,115}(9,86-9,50)=9,552.$$

L’itération pour trouver l’espérance de vie à partir des estimations de la table-type du model Ouest donne une estimation du taux de croissance (comme cela est expliqué plus en détail ci-dessous) de 3,065%, et l’estimation finale de l’espérance de vie apparaît dans la colonne 4 du tableau 1.

Tableau 1 : Espérances de vie par âge selon la méthode utilisée, Salvador, recensement de 1961

 

Age x	Méthode de Brass de la balance de la croissance démographique	Modèle Ouest de Princeton	Itérations successives
65	13,4	9,55	13,1
70	10,4	7,38	10,2
75	7,9	5,57	7,8
80	5,9	4,06	5,8
85	4,4	2,88	4,3

Comme le VIH/sida n’existait pas au Salvador en 1961, on peut utiliser les estimations dérivées de la table-type du modèle Ouest de Princeton, qui apparaissent dans la feuille de calcul intitulée Espérances de vie du classeur Excel pour calculer la complétude de la déclaration des décès. Cependant, pour mieux illustrer la méthode, le classeur Excel utilise la méthode itérative, bien que la comparaison des estimations qui figurent dans le tableau 1 (et celle des valeurs observées des taux de mortalité par âge dans l’intervalle ouvert 75 ans et plus avec les taux lissés) suggère plutôt que l’âge soit exagéré, ou que la complétude baisse au-delà de 75 ans. Dans un cas comme dans l’autre, ceci conduirait à une surestimation de la complétude.

Etape 3: Estimer le nombre de personnes qui atteignent l’âge x, et ceux qui atteignent le groupe d’âge x à x+4, d’après les décès déclarés

Le nombre de personnes qui atteignent l’âge x au cours de la période de référence (celle où sont déclarés les décès) se calcule à partir du nombre de décès dans chaque groupe d’âge, en utilisant le groupe d’âge ouvert de 75 ans et plus, le taux de croissance de 3,065%, et l’estimation de l’espérance de vie qui figure dans la quatrième colonne du tableau 1. Les résultats figurent en colonne 4 du tableau 2. Par exemple, l’estimation du nombre de personnes qui atteignent 70 ans au cours de la période de référence s’obtient comme suit :

$${\widehat{N}}_{75}=\text{}1360(\exp (0,03065\times 7,76)-{(0,03065\times 7,76)}^2/6)=1712,11$$$${\widehat{N}}_{70}=\text{}1712\exp (5\times 0,03065)+504\exp (2,5\times 0,03065)=2539,76.$$

Le nombre de personnes qui atteignent le groupe d’âge x à x+4 au cours de la période de référence est indiqué en colonne 5 du tableau 2. Par exemple, le nombre de personnes qui atteignent le groupe d’âge 20-24 ans se calcule comme suit :

$${}_5{\widehat{N}}_{20}=2,5(21542+18212)=99382,90.$$

Tableau 2 : Calcul du nombre de personnes atteignant le groupe d’âge x à x+4 d’après les décès déclarés et le recensement, et rapports des estimations, Salvador, recensement de 1961

Age	5Nx(tc)	5Dx	Est Nx	Est 5Nx	Obs 5Nx	c: 5Nx	c: A-xNx
0-4	214 089	6 909			214 089
5-9	190 234	610	35 431	163 158	190 234	0,8577	0,8879
10-14	149 538	214	29 832	138 071	149 538	0,9233	0,8946
15-19	125 040	266	25 396	117 344	125 040	0,9384	0,8885
20-24	113 490	291	21 542	99 383	113 490	0,8757	0,8778
25-29	91 663	271	18 212	83 962	91 663	0,9160	0,8783
30-34	77 711	315	15 373	70 677	77 711	0,9095	0,8690
35-39	72 936	349	12 897	59 098	72 936	0,8103	0,8584
40-44	56 942	338	10 742	49 112	56 942	0,8625	0,8741
45-49	46 205	357	8 903	40 525	46 205	0,8771	0,8781
50-54	38 616	385	7 307	33 049	38 616	0,8558	0,8785
55-59	26 154	387	5 913	26 567	26 154	1,0158	0,8892
60-64	29 273	647	4 714	20 398	29 273	0,6968	0,8295
65-69	14 964	449	3 445	14 962	14 964	0,9999	0,9779
70-74	11 205	504	2 540	10 630	11 205	0,9487	0,9487
75+	16 193	1 360

Etape 4: Estimer le nombre de personnes qui atteignent le groupe d’âge x à x+4 au cours de la période de référence, d’après le recensement de population

Dans ce cas particulier, comme les décès sont enregistrés au cours d’une seule année, le nombre de personnes qui atteignent le groupe d’âge x à x+4 au cours de la période de référence est simplement égal au nombre de personnes dans le groupe d’âge (c’est-à-dire que les effectifs figurant en colonne 6 sont les mêmes que ceux qui figurent en colonne 2 du tableau 2), car les multiplier par 1 ne les change pas.

Etape 5: Calculer les rapports des estimations faites à partir des décès déclarés aux estimations faites à partir du recensement de population

Les rapports des effectifs de personnes atteignant le groupe d’âge x à x+4 au cours de la période de référence, calculés en rapportant ceux obtenus d’après les décès déclarés sur ceux obtenus d’après le recensement, apparaissent en colonnes 7 et 8 du tableau 2. Par exemple, le calcul pour les groupes d’âge 65-69 ans et 65-74 ans donne :

$$\frac{{}_5{\widehat{N}}_{65}}{{}_5{N}_{65}}=\frac{14962}{14964}=0,9999$$$$\frac{{}_{10}{\widehat{N}}_{65}}{{}_{10}{N}_{65}}=\frac{14962+10630}{14964+11205}=0,9779.$$

Etape 6: Estimer la complétude de la déclaration des décès

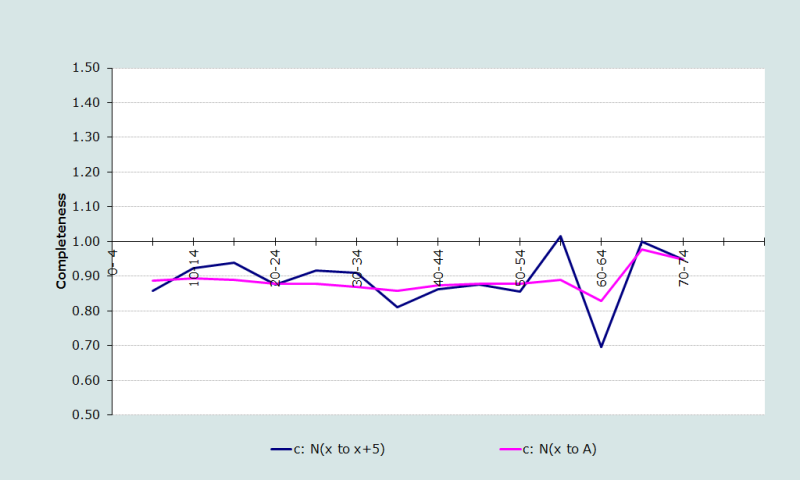
Dans cet exemple, l’estimation du taux de croissance fournie par l’application de la Méthode de Brass de la balance de l’accroissement démographique produit une série cohérente et satisfaisante des rapports. Cependant, nous proposons ici, à titre illustratif, de procéder à une itération pour trouver une nouvelle estimation du taux de croissance et de l’espérance de vie. Cette procédure permet de mettre dans un graphique les points correspondants aux rapports, comme le montre la figure 1.

Comme on n’observe aucune tendance nette, ni vers le haut ni vers le bas, dans cette figure 1, on peut déterminer le taux de croissance à partir des groupes d’âge de 5 à 74 ans, en minimisant les écarts à la moyenne à l’aide du module Solveur. La complétude se calcule à partir des rapports calculés pour les âges de 15 à 64 ans, afin d’éviter les fluctuations dues aux âges élevés (quoique cette méthode de calcul basée sur médiane et quartiles soit assez robuste aux fluctuations dans les groupes d’âge particuliers). Ce calcul donne une estimation de la complétude de 88%, et se fait comme suit :

$$\begin{array}{l}\text{}c=\left(0,5\times 0,8764+0,25(0,8575+0,9144)\right)\exp \left(0,0306(1961,34-1961,50)\right)\hfill \\ =0,8812\times 0,9957=87,7\%.\hfill \end{array}$$

 

Image

Figure 1 Completeness by age of registered deaths: El Salvador 1961

Etape 7: Estimer les taux de mortalité après correction pour tenir compte du sous-enregistrement des décès

La population moyenne, au milieu de la période de référence, se calcule à partir du recensement de population et du taux de croissance estimé entre les points extrêmes, soit 3,1%. Ces calculs figurent en colonne 2 du tableau 3. Par exemple, pour le groupe d’âge 15-19 ans, l’estimation se fait comme suit :

$${}_5{N}_{15}(t_m)=125040\times \exp (-0,0306(1961,34-1961,50))=125040e^{0,0306\times 0,16}=125655,7.$$

Puis les décès sont corrigés pour tenir compte du sous-enregistrement, en divisant le nombre de décès déclarés dans chaque groupe d’âge par l’estimation de la complétude. Ces nombres apparaissent en colonne 3 du tableau 3. Par exemple, pour le groupe d’âge 15-19 ans, le nombre se calcule à partir du nombre de décès déclarés (qui figure en colonne 3 du tableau 1, soit 266), comme suit :

$$\text{}\frac{266}{0,8768}=303,4.$$

Les personnes-années vécues soumises au risque (colonne 4 du tableau 3) se calculent comme le produit de la population moyenne, c’est-à-dire celle observée en milieu de la période de référence (colonne 2 du tableau 3) par la durée (exprimée en années) de la période de référence (au cours de laquelle les décès sont déclarés), qui dans ce cas est égale à 1 an.

Les taux de mortalité corrigés pour tenir compte du sous-enregistrement des décès (colonne 5 du tableau 3) se calculent en divisant les décès corrigés par les personne-années vécues. Par exemple, pour le groupe d’âge 15-19 ans, le taux de mortalité corrigé se calcule comme suit :

$$\text{}\frac{303,4}{125656}=0,00241.$$

   Tableau 3 : Calcul des taux de mortalité corrigés, Salvador, recensement de 1961

Age	Valeurs corrigées
	Population 5Nx(tm)	Décès 5Dx	Personnes- années PYL(x,5)	Taux de mortalité  5mx
0-4
5-9	191 171	696	191 171	0,0036
10-14	150 274	244	150 274	0,0016
15-19	125 656	303	125 656	0,0024
20-24	114 049	332	114 049	0,0029
25-29	92 114	309	92 114	0,0033
30-34	78 094	359	78 094	0,0046
35-39	73 295	398	73 295	0,0054
40-44	57 222	385	57 222	0,0067
45-49	46 433	407	46 433	0,0087
50-54	38 806	439	38 806	0,0112
55-59	26 283	441	26 283	0,0166
60-64	29 417	738	29 417	0,0248
65-69	15 038	512	15 038	0,0337
70-74	11 260	575	11 260	0,0505
75+	16 273	1 551	16 273	0,0944

Etape 8: Lissage par un modèle relationnel logit et une table-type de mortalité

Les estimations des quotients quinquennaux de mortalité des femmes, ₅q_x, se calculent à partir des taux de mortalité selon la formule classique, comme cela apparaît en colonne 2 du tableau 4. Par exemple, le quotient de 15 à 19 ans se calcule comme suit :

$${\text{}}_5{q}_{15}=\frac{5\times 0,00241}{1+2,5\times \text{}0,00241}=0,0120.$$

Les survivants de la table de la mortalité à l’âge x+5 se calculent de proche en proche à partir des survivants à l’âge x, selon la formule classique, comme cela apparaît en colonne 3 du tableau 4. Par exemple, les survivants à 20 ans se calculent comme suit :

$$l_{20}=0,9740(1-0,01198)=0,9623\text{.}$$

Tableau 4 : Calcul des taux de mortalité lissés à l’aide du modèle relationnel logit et d’une table-type de mortalité, Salvador, recensement de 1961

Age	Données observées				Lissage					Table de mortalité
	5qx	lx/l5	Obs Y(x)		Princeton Ouest ls(x)	Logit standard Ys(x)	Logit lissé Y(x)	Surviv. lissé l(x)		T(x)	e(x)	Taux lissé 5mx
0
5	0,0180	1			1,0000			1		61,254	61,3	0,0025
10	0,0081	0,9820	-1,9987		0,9890	-2,2506	-2,1834	0,9875		56,285	57,0	0,0019
15	0,0120	0,9740	-1,8122		0,9805	-1,9585	-1,8980	0,9780		51,371	52,5	0,0028
20	0,0144	0,9623	-1,6204		0,9681	-1,7060	-1,6511	0,9645		46,515	48,2	0,0036
25	0,0166	0,9484	-1,4560		0,9519	-1,4928	-1,4428	0,9471		41,736	44,1	0,0041
30	0,0227	0,9327	-1,3141		0,9337	-1,3226	-1,2765	0,9278		37,049	39,9	0,0047
35	0,0268	0,9115	-1,1658		0,9132	-1,1766	-1,1337	0,9061		32,464	35,8	0,0054
40	0,0331	0,8870	-1,0304		0,8899	-1,0447	-1,0048	0,8818		27,994	31,7	0,0065
45	0,0429	0,8577	-0,8980		0,8628	-0,9194	-0,8824	0,8538		23,655	27,7	0,0081
50	0,0550	0,8209	-0,7611		0,8299	-0,7925	-0,7583	0,8200		19,470	23,7	0,0111
55	0,0806	0,7757	-0,6204		0,7863	-0,6514	-0,6205	0,7757		15,481	20,0	0,0155
60	0,1180	0,7132	-0,4555		0,7289	-0,4946	-0,4672	0,7180		11,747	16,4	0,0235
65	0,1569	0,6290	-0,2640		0,6490	-0,3074	-0,2842	0,6384		8,356	13,1	0,0357
70	0,2263	0,5303	-0,0607		0,5427	-0,0856	-0,0674	0,5337		5,426	10,2	0,0570
75		0,4103	0,1814		0,4062	0,1898	0,2018	0,4005		3,090	7,7	0,0903
80					0,2545	0,5373	0,5414	0,2530		1,457	5,8	0,1405
85					0,1201	0,9956	0,9893	0,1215		0,521	4,3	0,2115

La transformation logit des probabilités de survie figure en colonne 4 du tableau 4. Par exemple à 20 ans, la transformation logit de l₂₀ se calcule comme suit :

$${\gamma }_{20}=0,5\ln \left(\frac{1-0,9623}{0,9623}\right)=-1,6204.$$

La transformation de la table de mortalité conditionnelle pour les femmes, calculée à partir de la famille Ouest des tables-type de Princeton au niveau d’espérance de vie e₀ = 60 ans (colonne 5 du tableau 4) apparaît en colonne 6 du même tableau. Comme on peut le voir sur la figure 2, le modèle Ouest semble ajuster correctement les données, sauf peut-être aux très jeunes âges.

 

Image

Figure 2 Observed logits and adjusted mortality rates against expected derived from the female West model life table, El Salvador, 1961

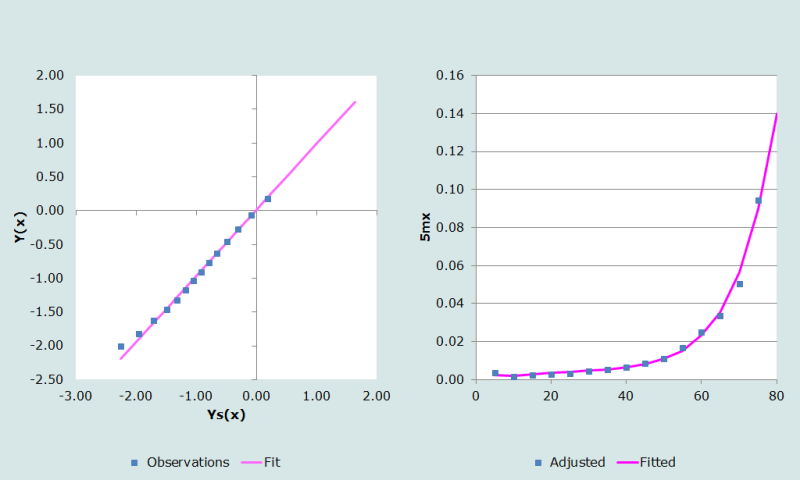
Les coefficients du modèle relationnel logit, α et β, se calculent comme la pente et l’ordonnée à l’origine de la droite de régression liant les transformations logit, qui figurent en colonne 4 et 6 du tableau 4, sur un intervalle d’âge choisi par l’utilisateur (entre 45 et 75 ans dans cet exemple), soit α = 0,0094 et β= 0,9754. On a choisi ici les âges de 45 à 75 ans, car l’ajustement aux âges élevés est important pour estimer l’espérance de vie au début de l’intervalle ouvert.

On applique ensuite ces coefficients à la transformation logit des probabilités de survie conditionnelle de la table-type afin de calculer les logits lissés, comme en colonne 7 du tableau 4. Par exemple, le logit lissé de la survie à l’âge de 20 ans se calcule comme suit :

$${\gamma }_{20}^{fitted}=0,0162+0,9774\times (-1,7060)=-1,6511.$$

Ces valeurs servent ensuite à calculer les survivants de la table de mortalité lissée, qui se trouvent en colonne 8 du tableau 4. Par exemple, la probabilité de survie à 20 ans se calcule comme suit :

$$l_{20}^{fitted}=\frac{1}{\exp \left(1+2\times (-1,6511)\right)}=0,9645.$$

Les années de vie cumulées au-delà de l’âge x, notées T_x, apparaissent en colonne 9 du tableau 4. Elles se calculent à partir des survivants lissés de la table de mortalité, selon la formule classique. Ces valeurs sont aussi utilisées pour produire les taux de mortalité lissés, qui apparaissent en colonne 11 du tableau 4. Par exemple, à l’âge de 80 ans :

$$T_{80}=0,521+\frac{5}{2}(0,253+0,1215)=1,457$$

 

$${}_5{m}_{80}^{fitted}=\frac{0,253-0,1215}{1,457-0,521}=0,1405\text{.}$$

Et l’espérance de vie à l’âge x se calcule en divisant les nombres de la colonne 9 par ceux de la colonne 8, comme cela est montré en colonne 10 du tableau 4. Par exemple, l’espérance de vie à 65 ans se calcule comme :

$$\text{}\frac{8,356}{0,6384}=13,089.$$

Diagnostics, analysé et interprétation

Contrôles et validation

L’exemple présenté ci-dessus était tiré du Manuel X (Division de la Population des NU 1984). Il donnait une estimation de la complétude d’environ 83%, à la fois en appliquant cette méthode et la Méthode de Brass de la balance de l’accroissement démographique. La différence entre les deux estimations du Manuel X et celle produite par cette application (89%) semble due essentiellement aux différences dans la méthode d’estimation de la population du groupe d’âge ouvert (A+). L’effet complet est contrebalancé, au moins dans une certaine limite, par une réduction de l’estimation (par rapport à l’estimation du Manuel X) due au fait que l’approche présentée ici trouve, par itération, un taux de croissance (3,02%) qui est plus élevé que celui qui est utilisé dans le Manuel X (2,87%). En conséquence, l’application de la méthode avec les estimations d’espérance de vie calculées à l’aide de la table-type du modèle Ouest de Princeton (colonne 3 du tableau 1) produit une estimation de la complétude de 85%.

Interprétation

Du fait qu’il n’y ait pas de tendance visible (ni montante ni descendante) sur le graphique de la figure 1, il n’y a aucune raison d’abaisser l’âge de début de l’intervalle ouvert. Cependant, si cela avait été nécessaire, il aurait été difficile de déterminer quelle estimation de la complétude retenir, car celle-ci est de 85% si on utilise l’intervalle ouvert de 70 ans et plus, mais de 76% avec l’intervalle ouvert de 65 ans et plus. La feuille de calcul ne permet pas à cet âge de début de l’intervalle ouvert d’être inférieur à 65 ans. Mais si on avait utilisé un intervalle ouvert de 60 ans et plus, l’estimation de la complétude aurait été supérieure à 76%. En règle générale, on recommande de ne pas s’arrêter à un âge finissant par zéro dans les populations qui font preuve d’une préférence marquée pour les chiffres ronds.

Dans l’ensemble, ces résultats indiquent que la complétude de la déclaration des décès est d’environ 85%, un peu moins que les 92% obtenus en appliquant la Méthode de Brass de la balance de l’accroissement démographique avec les mêmes données. Il est intéressant de noter que si l’on avait utilisé une estimation de l’espérance de vie dans les tables-type du modèle Ouest de Princeton basées sur le rapport des décès à 10-39 ans et à 40-59 ans (₃₀D₁₀ / ₂₀D₄₀) et un intervalle ouvert de 75 ans et plus, alors l’estimation de la complétude serait tombée à 85%, mais l’estimation de l’espérance de vie calculée à partir des taux lissés est plus proche de celle qui est obtenue par itération que de celles qui sont utilisées pour produire l’estimation de la complétude. Ceci suggère que la méthode n’est pas très sensible aux estimations de l’espérance de vie qui sont utilisées, surtout si l’intervalle ouvert commence à un âge élevé. 

Problèmes d’interprétation relatifs a la méthode

Source des données sur les décès déclarés

En général, on trouve deux types de problèmes concernant les données sur les décès : la question de la complétude (inférieure ou supérieure à 1), ce qui est la base de la méthode ; et la question de la complétude différentielle selon l’âge, qui peut entrainer un biais dans les estimations. Quoique l’approche générale reste essentiellement la même quelle que soit la source des données sur les décès, les différentes sources disponibles ont chacune leurs propres biais, qui peuvent affecter l’interprétation des résultats. On illustrera ce point par différents exemples, mais en général il convient de prêter attention aux biais suivants pour ce qui concerne les données sur les décès.

1) Données sur les décès de l’état civil

Si la répartition proportionnelle de la population entre les zones urbaines et rurales (ou une autre catégorie similaire) diffère significativement selon l’âge, et que la complétude de la déclaration des décès dans les zones urbaines est significativement supérieure à celle des zones rurales, alors l’hypothèse que la complétude est indépendante de l’âge sera vraisemblablement violée, et l’on observera une baisse de la complétude selon l’âge au-delà de 50 ans si une proportion importante de personnes migrent de l’urbain vers le rural au moment de la retraite. Si on ignore ce biais, et si le taux de croissance est estimé à l’aide du module Solveur, ne pas respecter l’hypothèse conduira à sous-estimer le niveau moyen de complétude.

2) Données sur les décès déclarés dans les recensements et les enquêtes ménage

Ces données sont potentiellement sujettes à trois problèmes:

• Si une proportion importante de ménages sont dissous suite au décès d’une personne clé (par exemple la personne qui assure les ressources du ménage), alors les décès de ces personnes risquent de n’être pas déclarés, ce qui induit une violation de l’hypothèse d’indépendance de la complétude avec l’âge. Si une proportion importante de décès de certains groupes d’âge se rapportent à des personnes qui ne vivent pas dans des ménages ordinaires (par exemple ceux qui vivent dans des maisons de retraite), la violation de l’hypothèse pourrait être encore plus forte. Cependant, ce problème ne se pose pas dans la plupart des pays en développement.
• Dans les cas où les jeunes adultes quittent le domicile familial quand ils grandissent, pour aller travailler en milieu urbain, il est possible qu’ils soient considérés comme membres de plusieurs ménages (ou bien d’aucun ménage), et que leurs décès soient déclarés plusieurs fois (ou jamais), ce qui conduit là encore à une violation de l’hypothèse de complétude de la déclaration uniforme selon l’âge. Dans ce cas, on pourrait en limiter l’impact en ignorant les données se rapportant à un groupe d’âge spécifique pour calculer la complétude.
• Erreurs sur la période de référence: lorsqu’il y a une confusion fréquente sur la période précise au cours de laquelle les décès doivent être déclarés, en plus des erreurs sur la date précise du décès, il peut arriver que l’on sous-estime, ou surestime, les décès. Si l’on peut supposer que ces biais sont indépendants de l’âge de la personne décédée, cette distorsion sera prise en compte dans l’estimation de la complétude, et ne posera pas de problème pour l’estimation finale des taux de mortalité corrigés.

3) Décès enregistrés dans les structures sanitaires

On ne sait que peu de choses sur la manière dont ces sources de données fonctionnent. Cependant, on peut supposer que la complétude dépendra de la répartition des structures sanitaires dans lesquelles ces données seront recueillies, et dans de nombreux pays en développement ce type de service sera vraisemblablement concentré en milieu urbain. Dans ce cas encore, si la proportion de la population vivant en milieu urbain, plutôt qu’en milieu rural, varie avec l’âge, alors on ne pourra pas faire l’hypothèse que la complétude est indépendante de l’âge. De plus, il est possible que certaines causes de décès soient plus fréquentes dans les structures sanitaires, et si ces causes sont importantes quantitativement et corrélées avec l’âge, on pourrait avoir une nouvelle violation de l’hypothèse de la complétude constante selon l’âge.

Dans tous les cas mentionnés ci-dessus, on devrait éviter d’ajuster le taux de croissance pour obtenir une séquence de rapports bien horizontale. Au contraire, il conviendra plutôt de s’assurer que l’estimation de c est calculée sur un intervalle d’âge qui exclut ceux pour lesquels la complétude de la déclaration des décès est exceptionnellement forte ou exceptionnellement faible.

Interprétation du diagnostic général

En pratique, les séquences des deux rapports : $${}_5\widehat{N}{}_x/{}_{5}N{}_x$$ et $${}_A\widehat{N}{}_x/{}_{A}N{}_x$$ sont affectées par les violations des hypothèses qui sous-tendent la méthode. Toutefois, la puissance de cette technique vient en partie de ce que la plupart des violations courantes des hypothèses vont produire des écarts caractéristiques et distincts par rapport à la droite horizontale qui est attendue, et dans certaines circonstances ces écarts pourront être interprétés. Voici quelques exemples :

a) taux de croissance erroné: Si r est trop élevé, la séquence des points tend presque linéairement avec l’âge vers la valeur sous-jacente de la complétude, et vice versa, comme le montre l’analyse de l’équation (1) ci-dessous. Cet effet sera plus fort pour les rapports dans les groupes d’âge quinquennaux, $${}_5\widehat{N}{}_x/{}_{5}N{}_x$$ que pour les âges cumulés $${}_A\widehat{N}{}_x/{}_{A}N{}_x$$<.

b) Exagération de l’âge déclaré: Il est courant que les parents qui déclarent le décès tendent à exagérer l’âge au décès du défunt, plus que les vivants ne le font lorsqu’ils déclarent leur propre âge au recensement. Ce biais produit une séquence de points dont la pente tend à augmenter, surtout après l’âge auquel cette exagération commence, et la séquence au-delà de ce point est marquée par une forte courbure vers le haut. Ce schéma peut se comprendre en examinant l’équation (1) ci-dessous : l’exagération de l’âge conduit non seulement à une augmentation du nombre de décès dans le groupe d’âge suivant, mais en plus le transfert d’un groupe à l’autre conduit à ce que ces décès soient multipliés par un coefficient exponentiel plus fort, quoique ce dernier biais soit de moindre importance. Un tel biais pourrait aussi être produit par une augmentation de la complétude de l’enregistrement des décès avec l’âge, au-delà d’un certain âge. Toutefois, en pratique ceci n’a pas été observé (Preston, Coale, Trussell et al. 1980).

c) Erreurs sur l’âge dans les estimations de la population, et erreurs de décompte variant selon l’âge: Ce type de biais se manifeste par une série erratique des rapports tout au long des âges de la vie. Comme la quantité $${}_5\widehat{N}{}_x$$ est de forme cumulative, elle tend à suivre d’assez près la distribution par âge de la population. Donc, si l’on observe des zigzags, il est vraisemblable que les pics soient associés à des âges faisant l’objet d’aversion ou de sous-enregistrement dans la population, et que les baisses soient associées à une préférence pour certains âge ou à un sur-enregistrement de la population. Si ces fluctuations sont indépendantes de l’âge, elles ne devraient pas particulièrement affecter les estimations de la complétude. John Blacker (Blacker 1988) a proposé d’utiliser d’autres groupes d’âge (comme 18-22, 23-27, etc.) pour éliminer ces zigzags, et a montré que ceci permettait de réduire les biais dans l’estimation de la pente lors de l’application de la Méthode de Brass de la balance de l’accroissement démographique. Cependant, lorsque ces distorsions sont systématiques, par exemple produites par des migrations en-deçà d’un certain âge, il peut être préférable d’exclure ces points pour l’estimation de la complétude.

On peut, en général, éliminer l’essentiel de l’effet de la surestimation de l’âge en commençant l’intervalle ouvert à un âge suffisamment jeune pour y confiner l’essentiel de la surestimation.

Afin de distinguer les séquences des rapports ayant une pente déclinante et qui sont dues à la baisse de la mortalité de celles qui sont dues au choix d’un taux de croissance trop élevé, on doit considérer d’autres sources de données pour déterminer quelle est l’explication la plus plausible. Si la mortalité de la population tend à diminuer, la médiane des rapports des effectifs cumulés, par exemple de 10 à 45 ans, devrait quand même permettre de fournir une estimation raisonnable de la complétude de l’enregistrement des décès. Même si cette méthode a de sérieux atouts et qu’elle est plus robuste aux écarts à la stabilité que ne l’est la Méthode de Brass de la balance de l’accroissement démographique, elle reste plus sensible que cette dernière à certains types d’erreurs sur l’âge. Il ne sera alors pas possible d’obtenir une seule estimation robuste de la complétude des données sur les décès, sauf si on peut confirmer par d’autres moyens que les hypothèses se vérifient, surtout l’hypothèse de la croissance démographique.

Description détaillée de méthode

Exposé mathématique

La méthode de Preston et Coale est un cas particulier de la Méthode de l’extinction des cohortes synthétiques, avec un taux de croissance r(x+) de la population au-delà de l’âge x identique pour tous les âges.  L’origine de la méthode remonte aux travaux pionniers de Paul Vincent (Vincent 1951) sur la méthode de l’extinction des cohortes, et aux travaux de Samuel Preston et Kenneth Hill (Preston et Hill 1980), qui fut améliorée par la suite (Preston, Coale, Trussell et al. 1980). Elle repose sur l’idée simple que le nombre de personnes d’un certain âge, survivantes à un certain moment, doit être égal au nombre de décès qui se produiront dans cette cohorte, jusqu’au moment où le dernier survivant sera décédé. Dans une population stable et fermée aux migrations, cette relation s’écrit 

$$N_x={\displaystyle \sum _{a=x}^{\varpi }{D}_a{e}^{r(a-x)}}$$

où $$D_a$$ sont les décès d’âge a pris au même instant que la population $$N_x$$, car dans une population stable et fermée, $$D_{a,t}$$, le nombre de décès d’âge a qui vont se produire dans t années après le moment où on réalise l’enregistrement des décès sera égal à $$D_a{e}^{rt}.$$.

Si, au lieu de $$D_a$$ on connait, $$D_a^r$$ le nombre de décès enregistrés d’âge x au dernier anniversaire, et si on estime la population d’âge x, c’est-à-dire $${\widehat{N}}_x$$  , par la quantité : $${\widehat{N}}_x={\displaystyle \sum }_{a=x}^{\varpi }{D}_a^r{e}^{r(a-x)}$$ , alors le rapport $${\widehat{N}}_x/N_x$$ (où $$N_x$$ est la taille de la population au milieu de l’intervalle au cours duquel on enregistre les décès) fournira une indication sur le pourcentage de décès au-delà de l’âge x qui sont enregistrés, soit c_x+. Si, de plus, la population d’âge x, soit $$N_x$$, est disponible à deux points dans le temps, on peut affiner l’estimation en tenant compte du taux de croissance r au cours de la période. Cependant, si le niveau de complétude est estimé pour calculer les taux de mortalité, alors la même correction s’appliquera de fait au numérateur comme au dénominateur, si bien qu’elle pourra être ignorée.

En pratique, on rencontre un problème pour calculer $${\widehat{N}}_x$$ car les décès $$D_a^r$$ ne sont pas toujours disponibles au-delà d’un certain âge (et même s’ils le sont, ils ont peu de chance d’être d’âge précis), c’est pourquoi on les regroupe au-delà de cet âge dans le groupe d’âge ouvert, soit$$D_{A+}^r$$ où A désigne le début de cet intervalle ouvert. Plusieurs méthodes ont été proposées pour résoudre ce problème. Par exemple, dans le Manuel X (Division de la Population des NU 1984: 136), on propose de faire l’hypothèse que le schéma de mortalité suit celui d’une des tables-types de mortalité de Princeton révisées (Coale, Demeny et Vaughan 1983). Dans ce cas, $${\widehat{N}}_A$$ se calcule comme suit 

$${\widehat{N}}_A=D_{A+}{e}^{rz(A)}$$

où

$$z(A)=a(A)+b(A)+c(A)e^{[D_{45+}/D_{10+}]}.$$

Les coefficients correspondants ont été tabulés (voir le tableau 123 dans : Division de la Population des NU. 1984: 137). On estime alors le rapport $$\text{}{D}_{45+}/D_{10+}\text{}$$ par le rapport $$\text{}{D}_{45+}^r/D_{10+}^r\text{}.$$

Il existe une alternative (Bennett et Horiuchi 1984), qui recommande d’estimer la population d’âge A par la formule suivante:

$${\widehat{N}}_A={\text{}}_{\infty }{D}_A\left(\exp \left(r\times e_A\right)-{\left(r\times e_A\right)}^2/6\right)$$

où l’espérance de vie à l’âge A (e_A) est interpolée au sein de la famille Ouest des tables-type de Princeton, à partir du rapport des décès déclarés entre les âges 10 et 40 ans et les âges 40 et 60 ans.

Puisque $${\widehat{N}}_x$$ peut être approché par: $$N_{x+5}{e}^{5r}+{}_{5}D{}_x^r{e}^{2.5r}$$ lorsque $${\widehat{N}}_A$$ a été estimé, on peut aussi estimer les $$\hspace{0.25em}{\widehat{N}}_x\hspace{0.25em}$$ à partir des décès $${}_{5}D{}_x^r.$$

Limites de la méthode

Les principales limites de la méthode ont été décrites ci-dessus, et sont prises en compte dans les feuilles de calcul : il faut que la population soit stable et fermée aux migrations. La méthode ne devrait pas être utilisée lorsque ces conditions ne sont pas vérifiées et que l’on s’en écarte trop. Un exemple d’utilisation abusive de la méthode est donné dans le classeur Excel intitulé SEG_South Africa_males. L’exemple provient d’Afrique du Sud, pour les décès déclarés entre le recensement de 2001 et l’enquête de communauté de 2007, un substitut au recensement. En prenant pour population au milieu de la période la moyenne des deux populations, on trouve une estimation de la complétude de 84% avec le même intervalle d’âge. Si on augmente à 35 ans l’âge minimal pour l’intervalle d’âge utilisé pour ajuster la ligne droite, on trouve une estimation de 86%, ce qui encore inférieur à l’estimation de 94% que l’on trouve avec la Méthode de l’extinction des cohortes synthétiques.

Cette méthode est plus vulnérable aux erreurs sur l’âge que la Méthode de Brass de la balance de l’accroissement démographique. En particulier, comme cela est mentionné ci-dessus, la tendance fréquente à exagérer les âges au décès déclarés (par rapport aux âges enregistrés au recensement) se manifestera par des points sur le graphique qui suivent une pente positive au-delà de l’âge à partir duquel l’exagération est forte. Dans de telles situations, il est préférable d’utiliser le taux de croissance fourni par la Méthode de Brass de la balance de l’accroissement démographique. De plus, comme cela a été montré ci-dessus, la méthode est aussi sensible au choix du groupe d’âge ouvert lorsque les données sont affectées par une forte préférence pour les âges ronds, ce qui est très souvent le cas avec les données de recensement.

Par contre, la méthode est moins vulnérable aux effets de déstabilisation résultants d’un changement rapide de la mortalité au cours du temps (Martin 1980). De plus, des simulations ont montré pour la Méthode de Brass de la balance de l’accroissement démographique que les biais résultant d’une baisse lente et régulière de la mortalité (comme le connaissent certains pays en développement en l’absence d’épidémies, de famines et de guerres) sont assez faibles (Rashad 1978).

En ce qui concerne les variations de la fécondité, celles-ci tendent à n’avoir qu’un faible impact sur les performances de la méthode, car elles n’affectent guère que les groupes d’âge les plus jeunes, ce qui n’a qu’une influence modérée sur les estimations de la complétude. Si nécessaire, ces groupes d’âge peuvent d’ailleurs être exclus pour calculer les taux de croissance et estimer la complétude.

Les migrations peuvent affecter la population des jeunes adultes (surtout entre 20 et 35 ans), mais elles ont moins d’effet sur les décès, qui sont concentrés aux âges élevés. Ignorer une immigration nette tendra à faire baisser la pente, et donc à surestimer la complétude de l’enregistrement des décès, ce qui se traduit par une sous-estimation des taux de mortalité. Ignorer une émigration nette aura l’effet inverse. Certains démographes conseillent d’ajuster une ligne droite jusqu’à l’âge de 5 ans pour limiter l’effet des migrations inconnues, en supposant que les différences entre la complétude de l’enregistrement des décès à ces jeunes âges et celles qui prévaut aux âges élevés a peu de chance d’induire de fortes distorsions, car la mortalité reste très faible entre 5 et 14 ans. Cependant, on peut douter que cette adaptation puisse réduire le biais de manière importante.

Une alternative consiste à confiner l’ajustement des points au-delà de 35 ans, de manière à éliminer l’essentiel de l’effet perturbateur des migrations. Mais souvent les données concernant les âges élevés sont de qualité plus médiocre, ce qui rend l’estimation de la complétude moins fiable. Il est possible que ces adaptions puissent produire de meilleures estimations que celles obtenues en ignorant carrément les migrations, mais malheureusement, très peu de recherches ont été conduites sur la précision des estimations de la complétude que produisent ces adaptations.

Techniquement parlant, si on dispose d’estimations fiables des migrations nettes par âge, on pourrait adapter la méthode en remplaçant le taux de croissance r par r – ₅i_x, où ₅i_x désigne le taux nette de migration pour le groupe d’âge x à x+4, l’âge étant pris au dernier anniversaire, pour calculer $${\widehat{N}}_x$$. Les variations selon l’âge de la complétude de l’enregistrement des décès peuvent induire une courbure dans la série de points du graphique. En conséquence, une des forces de cette méthode est de faire une vérification graphique : lorsque les points correspondants aux âges successifs sont à peu près alignés, on peut alors raisonnablement supposer que la complétude est constante selon l’âge. Et si certains ne le sont pas, on peut alors choisir de limiter l’intervalle d’âge aux points alignés pour calculer l’estimation de la complétude.

Autres lectures et références

Puisque cette méthode est un cas particulier de la méthode plus générale intitulée Méthode de l’extinction des cohortes synthétiques, on renverra le lecteur à cette section pour en savoir plus.

 

Bennett NG and S Horiuchi. 1984. "Mortality estimation from registered deaths in less developed countries", Demography 21(2):217-233. doi: https://dx.doi.org/10.2307/2061041

Blacker J. 1988. An Evaluation of the Pakistan Demographic Survey. Karachi: Pakistan Federal Bureau of Statistics.

Coale AJ, P Demeny and B Vaughan. 1983. Regional Model Life Tables and Stable Populations. New York: Academic Press.

Division de la Population des NU. 1984. Manuel X. Techniques indirectes d’estimation démographique. New York : Nations Unies, Département des affaires économiques et sociales internationales, ST/ESA/SER.A/81. https://unstats.un.org/unsd/demographic/standmeth/handbooks/Manuel_X-fr.pdf

Martin LG. 1980. "A modification for use in destabilized populations of Brass's Technique for estimating completeness of death registration", Population Studies 34:381-395. doi: https://dx.doi.org/10.2307/2175194

Preston SH, AJ Coale, J Trussell and M Weinstein. 1980. "Estimating the completeness of reporting of adult deaths in populations that are approximately stable", Population Index 46:179-202. doi: https://dx.doi.org/10.2307/2736122

Preston SH and KH Hill. 1980. "Estimating the completeness of death registration", Population Studies 34:394-366. doi: https://dx.doi.org/10.2307/2175192

Rashad HM. 1978. "The Estimation of Adult Mortality from Defective Registration Data." Unpublished PhD thesis, London: University of London.

UN Population Division. 2011. World Population Prospects: The 2010 Revision, Volume I: Comprehensive Tables. New York: United Nations, Department of Economic and Social Affairs, ST/ESA/SER.A/313. https://www.un.org/development/desa/pd/sites/www.un.org.development.desa.pd/files/files/documents/2020/Jan/un_2010_world_population_prospects-2010_revision_volume-i_comprehensive-tables.pdf

Vincent P. 1951. “La mortalite des vieillards”, Population 6:182–204. doi: https://dx.doi.org/10.2307/1524149