Estimation de la fécondité par la survie inverse
Description de la méthode
La survie inverse est une méthode d’estimation de la fécondité à partir des données recueillies dans un recensement ou une enquête en une seule vague, qui peut être utilisée même si aucune question n’a été posée directement concernant la fécondité. Dans une population fermée à la migration, la population à un âge x est composée des survivants des naissances survenues dans cette population il y a x années révolues. Il en résulte que le nombre de naissances survenues il y a x années peut être calculé si on peut estimer les probabilités de survie de la table de mortalité de la naissance à l’âge x (c’est-à-dire ). On parle aussi de projection rétrospective ou rétro-projection.
En ramenant la population à ce qu’était son effectif l’année de sa naissance et en divisant le nombre de naissances par une estimation de la population totale cette année-là, on obtient le taux brut de natalité, et en divisant par une estimation du nombre des femmes d’âge fécond, on obtient le taux global de fécondité. En combinant les estimations rétrospectives des naissances et des femmes selon l’âge avec des estimations, ou des hypothèses raisonnables, sur la distribution de la fécondité par âge, on peut aussi estimer l’indice synthétique de fécondité.
Les questions sur les naissances de l’année écoulée ou sur la date de naissance du dernier né des femmes ne permettent qu’une estimation de la fécondité actuelle. Les méthodes de survie inverse peuvent fournir des estimations de fécondité pour les 15 dernières années. En outre, à la différence des estimations de fécondités tirées d’histoires génésiques, qui ne sont généralement recueillies qu’auprès des femmes âgées de 15 à 49 ans, les estimations obtenues par la survie inverse ne sont pas tronquées de plus en plus sévèrement aux âges élevés à mesure qu’elles sont calculées pour des périodes plus anciennes. Une distribution des enfants par année d’âge permet de produire une série annuelle d’estimations de la fécondité. Toutefois, en pratique, les données sur l’âge recueillies dans les pays en développement sont rarement suffisamment précises pour qu’une série chronologique puisse être établie de façon fiable.
Précautions et mises en garde
Les méthodes décrites ici dépendent étroitement de la précision de la distribution par âge de la population déclarée. Des erreurs dans la distribution par âge, telles que l’omission de nourrissons et de jeunes enfants et l’attraction exercée par la déclaration de certains âges, peuvent avoir un impact important sur les résultats obtenus. Comme le note le Manuel X, « dans la mesure où les ensembles de données disponibles comportent bien trop fréquemment des erreurs ou des omissions de ce genre, il arrive souvent que les méthodes de la projection rétrospective ne permettent pas d’obtenir des estimations fiables de la fécondité. Leur utilité provient alors essentiellement du fait qu’elles fournissent des estimations originales de la fécondité qui permettent de mesurer de degré de vraisemblance des estimations qui ont été calculées par d’autres moyens » (Division de la Population des NU 1984).
Le sous enregistrement des nourrissons et des jeunes enfants est courant dans les recensements et les enquêtes des pays en développement. Ce sous dénombrement des enfants, en particulier ceux de deux ans ou moins, se traduit par des estimations trop basses de la fécondité dans la même proportion. Les méthodes de projection rétrospective tendent ainsi à sous-estimer la fécondité actuelle et donnent une impression exagérée de baisse de la fécondité.
En outre, une mauvaise déclaration des âges, en particulier l’attraction par certains âges, peut se traduire par des séries chronologiques erratiques des estimations de fécondité.
Des recherches sur la qualité des données par âge et sexe sont indispensables avant de procéder à des estimations de la fécondité par l’application d’une des méthodes de survie inverse. Celles-ci doivent être utilisées avec prudence s’il existe des doutes sur la qualité des données.
Bien que l’opération soit possible, il n’est généralement pas recommandé de procéder à des estimations de fécondité par projection rétrospective remontant à plus de 15 ans avant le recueil des données. La première raison est que la migration et le sous-enregistrement différentiel risquent de biaiser les estimations fondées sur la distribution par âge des adultes âgés de 15 ans ou plus. En outre, des estimations de fécondité remontant plus loin en arrière dépendent de plus en plus de la précision des évaluations de la mortalité des femmes âgées.
Comme les résultats dépendent des hypothèses faites sur la survie, ils sont peu sensibles aux hypothèses sur la mortalité des enfants ou des femmes âgées de moins de 65 ans. Par exemple, si la probabilité de décéder d’un enfant né il y a une douzaine d’années était de 20 % et était sous-estimée d’un quart (soit une probabilité de 16 %), il en résulte une surestimation du nombre de naissances de (100 – 16)/(100 – 20), donc seulement de 5 %. De même, la probabilité de décéder de la mère a peu de chances d’être largement supérieure à 20 %, même si celle-ci était âgée à la naissance de son enfant. Si cette probabilité était sous-estimée d’un quart, la fécondité ne serait surestimée que de 4,8 %. En outre, si les bais dans les estimations de mortalité vont dans la même direction pour les enfants et les mères, les erreurs qui en résultent dans les estimations de fécondité se compensent et s’annulent partiellement.
Méthode 1 : Estimation du taux brut de natalité par période quinquennale
Données nécessaires et hypothèses
Tableaux de données nécessaires
Pour calculer les taux moyens de natalité pour les périodes quinquennales précédant le recensement ou l’enquête, les données suivantes sont nécessaires :
- la population recensée âgée de moins de 15 ans, classée par groupes d’âge quinquennaux ;
- la population totale recensée à deux dates, ou la population totale recensée à un seule date et une estimation du taux de croissance ; et
- des estimations de la survie des enfants tirées de tables de mortalité, 5L0, 5L5 et 5L10.
Hypothèses importantes
La population est supposée avoir été fermée à la migration pendant toute la période couverte par les estimations par rétroprojection. Toutefois, comme les enfants migrent généralement avec leur mère, les erreurs au numérateur et au dénominateur des taux estimés se compensent largement. Le biais n’est important que si les flux migratoires sont abondants et que les migrants ont une fécondité différente du reste de la population.
Application de la méthode
Etape 1 : Calculer les survivants de la table de mortalité des enfants
Pour projeter rétrospectivement la population des trois groupes quinquennaux 0-4, 5-9 et 10-14 ans, on n’a besoin que des valeurs de 5L0, 5L5 and 5L10, les personnes-années vécues par la population stationnaire entre la naissance et 5 ans, et entre 5 et 10 ans, et 10 et 15 ans, respectivement. La source de ces mesures peut être une table de mortalité effectivement construite pour la population étudiée ou une table-type jugée adéquate (par exemple une des tables-types régionales de Princeton). Etant donné le haut degré d’agrégation entre les âges, on peut supposer que la mortalité est constante au long de chaque période quinquennale précédant le recensement ou l’enquête. Si la mortalité est surestimée, la fécondité sera surestimée (puisque la population dénombrée sera constituée des survivants de cohortes de naissances trop importantes) et vice versa.
Comme la mortalité évolue rapidement au cours de la première année de vie, 5L0 doit être calculé comme 5L0 = 1L0 + 4L1 si on utilise une table de mortalité effective du pays considéré. Si cette table fait la distinction entre filles et garçons, une table doit être calculée pour les deux sexes réunis moyennant une hypothèse appropriée sur le rapport de masculinité à la naissance. Soit la formule
où lmx et lfx sont les valeurs de lx pour les garçons et les filles respectivement, et S0 est le rapport de masculinité à la naissance (nombre de naissances de garçons pour 100 naissances de filles).
Si une table-type de mortalité est utilisée pour représenter la mortalité dans l’enfance, 5L0 , 5L5, and 5L10 sont obtenus par interpolation entre les valeurs appropriées dans la série des tables types.
Etape 2 : Estimation des populations au milieu de la période
Pour estimer des taux annuels de natalité pour les trois périodes quinquennales précédant le recensement, il faut disposer d’une estimation de la population totale au milieu de chacune des trois périodes. En l’absence d’une information détaillée directement utilisable (par exemple les résultats d’un recensement réalisé 10 ans plus tôt), et étant donné l’inévitable perte de précision due à l’agrégation des effectifs de population et de la mortalité en groupes quinquennaux, une estimation précise n’est pas nécessaire. Le mode le plus facile d’estimation de la population totale d’années auparavant, N(t-d), où d = 2,5 ans, 7,5 et 12,5, est de supposer un taux de croissance constant, r, et de l’appliquer à la population dénombrée au temps t, N(t), soit
Le taux de croissance, r, peut être estimé à partir d’informations sur l’effectif de la population totale, P, à deux points du temps, t0 et t1 , de sorte que
Ainsi, par exemple, la population 2,5 ans avant le recensement le plus récent est égale à
N(t-2.5)= N(t).exp(-2.5r)
ce qu’on peut étendre aux estimations de la population à d’autres points du temps.
Etape 3 : Estimer les naissances de chaque période quinquennale antérieure au recensement
Soit B(t – 5,t) le nombre de naissances survenues chaque année au cours de la période t – 5 à t années avant le recensement, où t=0, 5 ou 10. Soit aussi 5Nx(t) la population dénombrée âgée entre x et x + 5 ans à la date de recensement. Il s’ensuit que le nombre moyen de naissances dans chacune des périodes quinquennales de t-5 à t est égal à
B(t-5,t) = 5N0(t).l0/5L0
B(t-10,t-5) = 5N5(t).l0/5L5
et
B(t-15,t-10) = 5N10(t).l0/5L10
Le taux brut de natalité (en anglais, Crude Birth Rate, CBR) de chaque période est alors calculé en divisant le nombre de naissances de chaque période par la population correspondante en milieu de période, telle que calculée à l’étape 2. Soit
et de même pour les périodes antérieures.
Exemple
Les données du recensement de 2008 au Cambodge nous permettent d’illustrer les principes de l’estimation de la fécondité par la projection rétrospective.
Etape 1 : Calculer les survivants de la table de mortalité des enfants
La série des survivants est tirée de la table de mortalité de l’OMS pour le Cambodge en 2000. Les valeurs de nLx (sexes réunis) dans cette table de mortalité sont présentées au tableau 1 pour une racine de 100 000.
Tableau 1 Valeurs tirées de la table de mortalité de l’OMS pour le Cambodge, 2000
Age | n | x | lx | dx | nLx |
|---|---|---|---|---|---|
<1 | 1 | 0 | 100 000 | 7 956 | 94 431 |
1-4 | 4 | 1 | 92 044 | 2 684 | 361 734 |
5-9 | 5 | 5 | 89 360 | 887 | 444 581 |
A partir de ces données, on peut calculer les grandeurs suivantes
Etape 2 : Estimation des populations au milieu de la période
D’après les échantillons des recensements cambodgiens diffusés par IPUMS International, le Cambodge comptait 11 412 540 habitants le 3 mars 1998. Le 3 mars 2008, c’est 13 401 210. La population de moins de 5ans en 2008 est de 1 736 790 et celle de 5-9 ans 1 472 470.
Comme les recensements ont été réalisés précisément à 10 ans d’écart, le taux de croissance intercensitaire est égal à
pour 100 par an.
La population 2,5 ans et 7,5 ans avant le second recensement est estimée à :
Etape 3 : Estimer les naissances de chaque période quinquennale antérieure au recensement
Le nombre estimé de naissances pour chacune des périodes des cinq années précédant le recensement est égal à
B(t-5,t) = 1 736 790 × 0,21922 = 380 739.
Pour les cinq années précédentes, c’est
B(t-10,t-5) =1 472 471 × 0,22493 = 331 202.
En divisant les naissances par la population au milieu de la période, on obtient des taux bruts de natalité de 29,6 naissances pour 1000 pour le Cambodge en 2003-2008 et 27,9 naissances pour 1000 en 1998-2003.
L’ordre de grandeur de ces taux est comparable à ceux de l’US Census Bureau (28 en 2000 et 27 en 2005), et de la Division de la Population des NU (25,1 naissances pour 1000 en 2000-2005. Les estimations par la projection rétrospective suggèrent cependant une légère hausse de la fécondité pendant les années 1990. Il se pourrait que ce résultat soit faux et qu’il résulte d’erreurs dans les estimations initiales de la population ou au choix d’une table de mortalité inappropriée.
Méthode 2 : Estimation du taux global de fécondité et de l’indice synthétique de fécondité
La seconde application du concept de survie inverse décrite ici permet d’obtenir des estimations du taux global de fécondité et de l’indice synthétique de fécondité jusqu’à 15 ans avant le recensement ou l’enquête. Pour calculer le taux global de fécondité, il suffit d’estimer rétrospectivement la taille de la population adulte féminine à partir du nombre de femmes dénombrées, en tenant compte de la mortalité adulte. Mais pour calculer l’indice synthétique de fécondité, il ne suffit pas de connaître le nombre de naissances chaque année, mais aussi l’âge des mères de ces enfants. Une façon relativement simple de procéder, si cette information n’est pas disponible, consiste à répartir les naissances par groupe d’âge des mères d’après des estimations indépendantes de la distribution par âge de la fécondité.
Données nécessaires et hypothèses
Tableaux de données nécessaires
Pour le calcul du taux global de fécondité par année, les données suivantes sont nécessaires :
- Des tableaux de la population (sexes réunis) de 0 à 14 ans par année d’âge.
- Des tableaux de la population féminine de 15 à 64 ans par groupes d’âges quinquennaux.
- Les survivants des tables de mortalité des cohortes, Lx, pour les enfants de 0 à 14 ans (sexes réunis)
- Les probabilités de survie, 5Lx-5/5Lx des femmes adultes pour chacune des trois périodes quinquennales précédant le recensement ou l’enquête.
La mise en œuvre de la méthode dans le dossier Excel associé est possible avec des estimations de mortalité obtenues soit par référence aux paramètres de période α et β des tables-types relationnelles appropriées, soit à partir des valeurs calculées 5q0 (pour les enfants) et 45q15 (pour les femmes adultes) pour chacune des trois périodes quinquennales précédant le recensement ou l’enquête.
Pour estimer l’indice synthétique de fécondité, il faut aussi disposer
- soit d’une seule distribution de la fécondité par âge supposée applicable à l’ensemble de la période couverte par nos estimations,
- soit de deux distributions de la fécondité par âge, l’une applicable à une date raisonnablement proche du recensement ou de l’enquête et l’autre à une date antérieure d’environ 15 ans.
Les calculs peuvent être menés à partir d’une série de taux de fécondité ou à partir des paramètres d’un modèle relationnel de Gompertz ajusté à un schéma type de fécondité.
Seule la forme estimée de la distribution de fécondité est fondée sur ces schémas de fécondité. C’est le nombre estimé de naissances rapporté à la population des femmes d’âge fécond qui détermine presque entièrement les estimations du taux global et de l’indice synthétique de fécondité.
Hypothèses importantes
La population est supposée avoir été fermée à la migration pendant toute la période couverte par les estimations par rétroprojection. Toutefois, comme les enfants migrent généralement avec leur mère, les erreurs au numérateur et au dénominateur des taux estimés se compensent largement. Le biais n’est important que si les flux migratoires sont abondants et que les migrants ont une fécondité différente du reste de la population.
Application de la méthode
Etape 1 : Estimer le nombre de naissances chaque année précédant le recensement
La population recensée à l’âge x est composée des survivants des naissances qui sont survenues au cours de la période de 12 mois centrée sur la date x+0,5 ans avant le recensement. Algébriquement,
Dans ce calcul, la mesure des survivants, cLx, est prise dans une cohorte. Elle dépend de la mortalité aux âges successifs dans les années successives conduisant au recensement. Il se peut que les estimations par cohorte de la mortalité soient tirées du recensement ou de l’enquête utilisé pour estimer la fécondité. Ce peuvent être des estimations indirectes à partir des données sur les enfants déjà nés et les enfants survivants, dans le cas d’un recensement, ou des estimations directes tirées d’une analyse par cohorte des histoires génésiques, dans le cas d’une enquête sur la fécondité. Brass (1979) décrit une procédure simple pour estimer directement Lx à partir des proportions d’enfants survivants selon le groupe d’âge de leur mère.
Si on ne dispose pas de taux de survie par cohorte, ceux-ci peuvent être tirés d’estimations de la mortalité du moment par année d’âge pour chacune de périodes quinquennales précédant le recensement ou l’enquête.
Si on travaille avec un système logit relationnel de tables-types de mortalité, on doit définir αT et βT comme paramètres générant une table de mortalité pour la période T, où T=0 désigne la période 0-4 ans avant le recensement, T=5 la période 5-9 ans avant et T=10 la période 10-14 ans avant. Pour un standard donné, désigné par l’exposant s,
(1)
où lx ou xp0 désigne la proportion de survivants de la naissance à l’anniversaire x dans une table de mortalité de racine 1. L’équation 1 implique que
et que
(2)
Au-delà de la première année de vie, on peut approximer Lx,T, les personnes années vécues entre x et x+1 dans la période T en supposant que la survie recule linéairement sur une échelle logistique, et donc que le logit de Lx,T est la moyenne de Yx,T et Yx+1,T. De l’équation 2
(3)
Les valeurs de lx dans les réseaux de tables-types de mortalité sont souvent données par année d’âge jusqu’à 5 ans, puis de cinq en cinq ans. Si c’est le cas pour les enfants de 5 ans ou plus, on peut supposer que le logit de la fonction de survie recule linéairement sur l’ensemble de l’intervalle d’âge x à x+5. Ainsi par exemple, si une table de mortalité donne des valeurs pour x=5 et x=10, la valeur estimée de L9,T est donnée par
Pour la première année de vie, on doit tenir compte de la concentration des décès dans les premiers jours et les premières semaines. Dans les populations où la mortalité est moyenne ou élevée, on peut approximer les personnes-années vécues dans la première année par
(4)
Les probabilités de survie d’un âge au suivant, Px,T, au cours de la période T, sont tirés du rapport entre les valeurs successives de Lx,T :
(5)
Une fois obtenue la série des enfants survivants par année d’âge et périodes quinquennales, que ce soit par la procédure qui vient d’être indiquée ou par une autre, une estimation des survivants par année d’âge par cohorte annuelle peut être calculée comme suit. On rappelle que Pa,T est la probabilité de survie entre les âges a et a+1 au cours de la période T (où T=0, 5 ou 10, selon qu’il s’agit de la période 0-4, 5-9 ou 10-14 ans avant le recensement). On définit Sa,t la probabilité de survie entre les âges a et a+1 au cours de la période t à t+1 années avant le recensement, 0 ≤ t ≤ 14. En utilisant l’interpolation linéaire pour estimer la survie pour les années intermédiaires
La proportion de naissances survenues x à x+1 années plus tôt qui survivent au moment du recensement, cLx, peut alors être calculée comme
(6)
Le nombre de naissances de chaque année avant le recensement, centré sur le point médian de cette année-là (c’est-à-dire 6 mois avant la date du recensement), est donc
où Nx désigne le nombre d’enfants âgés de x déclarés au recensement.
Etape 2 : Estimer les populations en milieu d’année des femmes par groupe quinquennal d’âge
Le calcul de la survie des femmes âgées de 15 à 64 ans au moment du recensement est simple à réaliser car la mortalité est généralement faible aux âges adultes. Des estimations même approximatives de la mortalité suffisent donc pour une estimation satisfaisante de la population passée à partir de la population recensée.
La variation absolue de la mortalité au fil des âges dans un groupe quinquennal d’âge est faible. On peut donc approximer 5Lx par une interpolation linéaire entre Yx et Yx+5. Ceci signifie qu’on peut estimer la survie entre les groupes d’âge quinquennaux au temps T (avec T= 5, 10 et 15) comme
(7)
En débutant avec la population recensée en T = 0, on peut calculer le nombre de femmes dans chaque groupe quinquennal d’âge T + 5 ans avant le recensement à partir du nombre en T :
(8)
En outre, comme la structure par âge d’une population ne change que lentement, on peut calculer les populations des femmes âgées de 10-14, 15-19, …, 60-64 ans pour chacune des années avant la date du recensement par interpolation linéaire entre les estimations de populations 0, 5, 10 et 15 ans avant le recensement produites grâce à l’équation 8. Par exemple, pour estimer le nombre de femmes âgées de 20-24 ans 8,5 ans avant le recensement, la formule serait
Etape 3 : Calculer les taux globaux de fécondité
Le taux global de fécondité pour l’année centrée sur x-0,5 ans avant le recensement est
où le dénominateur est le nombre total de femmes âgées de 15 à 49 ans au point médian de l’année au cours de laquelle les naissances sont survenues.
Etape 4 : Estimer les taux par âge et l’indice synthétique de fécondité
Au-delà du calcul des taux globaux de fécondité, une extension naturelle consiste à utiliser un schéma de distribution de la fécondité par âge dans la population étudiée pour estimer l’indice synthétique de fécondité par une procédure analogue à celle de la standardisation indirecte.
Ce schéma de fécondité peut provenir de données sur les naissances récentes recueillies dans le même recensement que celui analysé par les méthodes de projection rétrospective. Comme on n’en tirera que des informations sur la distribution par âge de la fécondité, il n’est pas nécessaire d’ajuster les données pour tenir compte des erreurs sur la période de référence. Si une autre distribution est connue à partir d’un recensement ou d’une enquête antérieur (si possible d’environ 15 ans) dans la même population, on peut interpoler entre les deux distributions, ou extrapoler si nécessaire, afin d’estimer la forme de la distribution de la fécondité pour chacune des années dont on souhaite estimer l’indice synthétique de fécondité.
Mais même si la fécondité a changé, il n’est pas essentiel d’avoir deux distributions de fécondité, car la distribution par âge de la fécondité évolue graduellement et les estimations de l’indice synthétique sont peu sensibles à la précision des hypothèses sur la forme de la courbe de fécondité. Aussi une seule distribution (de préférence vers le milieu de la période d’estimation) suffit-elle.
Si, pour estimer la fécondité, on a utilisé un modèle relationnel de Gompertz, en combinaison avec le standard choisi, les paramètres α et β calculés lors de l’estimation de la fécondité définissent la forme de la courbe de fécondité. En conséquence, les valeurs de α et β peuvent être utilisées pour déterminer la forme de la (des) courbe(s) de fécondité utilisées dans l’estimation de l’indice synthétique.
Après avoir estimé la proportion de la fécondité totale qui survient dans chaque groupe d’âge pour chaque année antérieure au recensement, on peut appliquer ces proportions à la population des femmes de chaque groupe d’âge chaque année pour estimer le nombre de naissances qu’auraient eu les femmes de ce groupe d’âge si l’indice synthétique avait été égal à un enfant par femme.
Donc, une fois qu’on a choisi une courbe de fécondité (ramenée à un indice synthétique égal à 1), 5f*a,x+0.5, pour chaque groupe d’âge (a=15, 20, …, 45) pour chacune des 15 années (x) antérieures au recensement, le nombre de naissances attendu des femmes de chaque groupe d’âge pour chaque année est donné par
Il s’ensuit que le nombre total de naissances qui serait survenu l’année x, si l’indice synthétique avait été égal à 1, est de
Mais l’étape 2 a permis d’estimer le nombre effectif de naissances chaque année, Bx+0.5. L’indice synthétique de fécondité estimé pour chaque année est donc égal au rapport entre B et B*
On peut obtenir des estimations des taux de fécondité par âge pour l’année en multipliant les taux proportionnels, 5f*a,x, pour chaque groupe d’âge (a) et chaque année (x) par l’estimation de l’indice synthétique pour cette année. On remarquera cependant que ces résultats se contentent de reproduire la distribution de fécondité par âge introduite dans les calculs : la méthode ne donne pas de nouvelle information sur la distribution par âge de la fécondité.
Exemple
L’exemple, mis en œuvre dans le dossier Excel joint, consiste à estimer l’évolution de la fécondité au Cambodge à partir du recensement de 2008. L’échantillon de microdonnées est celui mis à disposition par IPUMS International et la date de référence du recensement est le 3 mars 2008. Dans une notation décimale, cette date correspond à 2008,17.
Les nombres d’enfants âgés de moins de 15 ans par année d’âge, et les nombres de femmes âgées de 10 à 64 ans par groupe quinquennal tirés des données figurent au tableau 2.
Tableau 2 Nombres d’enfants par année d’âge, et de femmes par groupe quinquennal, Cambodge, recensement de 2008
Age | Enfants | Groupe d’âge | Femmes |
|---|---|---|---|
0 | 281 260 | 10-14 | 815 930 |
1 | 261 320 | 15-19 | 780 320 |
2 | 268 410 | 20-24 | 697 160 |
3 | 286 810 | 25-29 | 626 430 |
4 | 278 990 | 30-34 | 361 650 |
5 | 293 760 | 35-39 | 435 880 |
6 | 293 490 | 40-44 | 393 760 |
7 | 302 060 | 45-49 | 352 520 |
8 | 315 970 | 50-54 | 294 280 |
9 | 267 190 | 55-59 | 230 200 |
10 | 326 980 | 60-64 | 160 590 |
11 | 280 260 | ||
12 | 354 120 | ||
13 | 356 920 | ||
14 | 354 830 |
La mortalité pour la période de cinq ans précédant le recensement est tirée des tables de mortalité 2009 OMS pour le Cambodge. Les survivants aux anniversaires x, ainsi que les logits correspondants, pour les enfants de moins de 15 ans (sexes réunis) et pour les femmes de 10 à 65 ans figurent au tableau 3.
Tableau 3 Table de mortalité OMS pour le Cambodge en 2009 utilisée comme standard
Enfants | l(x) | Logit, Y(x) |
|---|---|---|
0 | 1,0000 | |
1 | 0,9320 | -1,3085 |
5 | 0,9125 | -1,1723 |
10 | 0,9048 | -1,1256 |
15 | 0,8997 | -1,0968 |
Femmes | ||
10 | 0,9138 | -1,1805 |
15 | 0,9099 | -1,1561 |
20 | 0,9049 | -1,1266 |
25 | 0,8980 | -1,0875 |
30 | 0,8889 | -1,0399 |
35 | 0,8760 | -0,9774 |
40 | 0,8603 | -0,9089 |
45 | 0,8419 | -0,8361 |
50 | 0,8179 | -0,7511 |
55 | 0,7847 | -0,6467 |
60 | 0,7374 | -0,5161 |
65 | 0,6732 | -0,3613 |
Cette table de mortalité a été utilisée comme standard sur lequel ajuster des tables types de mortalité relationnelles pour les enfants et les adultes séparément pour les périodes antérieures de 5-9 et 10-14 ans au recensement aux tables de mortalité de l’OMS pour le Cambodge en 2000 et 1990. Les valeurs ajustées de α et β pour les enfants et les adultes figurent au tableau 4.
Tableau 4 Paramètres des tables types de mortalité relationnelles pour les périodes quinquennales avant le recensement de 2008, la table de mortalité OMS 2009 pour le Cambodge étant le standard
|
| Période avant le recensement (années) | ||
|---|---|---|---|---|
|
| 0-4 | 5-9 | 10-14 |
Enfants | α | 0,00 | 0,22 | 0,35 |
β | 1,00 | 1,10 | 1,17 | |
|
|
|
| |
Adultes | α | 0,00 | 0,08 | 0,00 |
| β | 1,00 | 0,97 | 0,87 |
Les estimations des taux de fécondité par âge pour mi-1997 et mi-2007 sont empruntées aux Perspectives de Population Mondiale de la Division de la Population des NU (révision de 2010). Elles figurent au tableau 5.
Tableau 5 Taux de fécondité pour le Cambodge utilisés dans la projection rétrospective
Année | ||
|---|---|---|
Groupe d’âge | 1997,5 | 2007,5 |
15-19 | 0,053 | 0,042 |
20-24 | 0,197 | 0,154 |
25-29 | 0,214 | 0,148 |
30-34 | 0,184 | 0,112 |
35-39 | 0,133 | 0,071 |
40-44 | 0,068 | 0,030 |
45-49 | 0,013 | 0,003 |
Etape 1 : Estimer le nombre de naissances chaque année précédant le recensement
En appliquant les équations 3 et 4 aux valeurs logit du standard présenté au tableau 3, en utilisant les valeurs de α et β du tableau 4, on obtient les estimations de Lx,T et Px,T qui figurent au tableau 6.
Tableau 6 Calcul des survivants et des probabilités de survie des cohortes par âge, Cambodge 1983-2008
x | Lx,0 | Lx,5 | Lx,10 | Px,0 | Px,5 | Px,10 | cLx |
|---|---|---|---|---|---|---|---|
0 | 0,9524 | 0,9439 | 0,9397 | 0,9524 | 0,9439 | 0,9397 | 0,9524 |
1 | 0,9298 | 0,9170 | 0,9106 | 0,9763 | 0,9716 | 0,9691 | 0,9298 |
2 | 0,9252 | 0,9112 | 0,9039 | 0,9951 | 0,9936 | 0,9926 | 0,9252 |
3 | 0,9197 | 0,9041 | 0,8958 | 0,9941 | 0,9923 | 0,9910 | 0,9181 |
4 | 0,9145 | 0,8974 | 0,8881 | 0,9944 | 0,9926 | 0,9914 | 0,9104 |
5 | 0,9118 | 0,8939 | 0,8840 | 0,9970 | 0,9960 | 0,9954 | 0,9049 |
6 | 0,9102 | 0,8919 | 0,8818 | 0,9983 | 0,9978 | 0,9974 | 0,9003 |
7 | 0,9087 | 0,8899 | 0,8795 | 0,9983 | 0,9978 | 0,9974 | 0,8954 |
8 | 0,9071 | 0,8879 | 0,8771 | 0,9983 | 0,9977 | 0,9973 | 0,8911 |
9 | 0,9056 | 0,8858 | 0,8747 | 0,9983 | 0,9977 | 0,9973 | 0,8871 |
10 | 0,9043 | 0,8842 | 0,8728 | 0,9986 | 0,9981 | 0,9978 | 0,8834 |
11 | 0,9033 | 0,8828 | 0,8713 | 0,9989 | 0,9985 | 0,9983 | 0,8801 |
12 | 0,9022 | 0,8815 | 0,8698 | 0,9989 | 0,9985 | 0,9983 | 0,8767 |
13 | 0,9012 | 0,8802 | 0,8682 | 0,9989 | 0,9985 | 0,9982 | 0,8741 |
14 | 0,9002 | 0,8789 | 0,8667 | 0,9989 | 0,9985 | 0,9982 | 0,8719 |
La survie de cohorte jusqu’à la date du recensement pour les enfants âgés de 0 à 14 ans est ensuite estimée à partir des équations 5 et 6 (dernière colonne du tableau 6).
Enfin, le nombre de naissances pour chaque année antérieure au recensement est obtenu en divisant le nombre d’enfants recensés en 2008 à chaque âge par la valeur appropriée de cLx. (Tableau 7).
Tableau 7 Nombre estimé de naissances pour chacune des 15 années précédant le recensement de 2008 au Cambodge.
Milieu d’année précédant la date du recensement | Naissances |
|---|---|
2007,67 | 295 328 |
2006,67 | 281 062 |
2005,67 | 290 118 |
2004,67 | 312 409 |
2003,67 | 306 453 |
2002,67 | 324 644 |
2001,67 | 325 997 |
2000,67 | 337 355 |
1999,67 | 354 583 |
1998,67 | 301 184 |
1997,67 | 370 118 |
1996,67 | 318 451 |
1995,67 | 403 924 |
1994,67 | 408 337 |
1993,67 | 406 976 |
Etape 2 : Estimer les populations en milieu d’année des femmes par groupe quinquennal d’âge
Les probabilités de survie des femmes par groupe quinquennal d’âge (Tableau 8) sont obtenues en appliquant les valeurs de α et β pour chaque période de cinq ans (tableau 4) aux logits du standard (tableau 3), au moyen de l’équation 7.
Tableau 8 Probabilités de survie, 5Px,T , par groupe quinquennal d’âge et période de cinq ans avant le recensement, Cambodge 1993-1998
Groupe d’âge | T=0 | T=5 | T=10 |
|---|---|---|---|
10-14 | 0,9951 | 0,9942 | 0,9945 |
15-19 | 0,9935 | 0,9922 | 0,9927 |
20-24 | 0,9912 | 0,9895 | 0,9902 |
25-29 | 0,9878 | 0,9855 | 0,9866 |
30-34 | 0,9838 | 0,9810 | 0,9826 |
35-39 | 0,9804 | 0,9772 | 0,9793 |
40-44 | 0,9752 | 0,9714 | 0,9744 |
45-49 | 0,9658 | 0,9609 | 0,9654 |
50-54 | 0,9501 | 0,9438 | |
55-59 | 0,9271 |
Les estimations de population des femmes par groupe quinquennal d’âge 5, 10 et 15 ans avant le recensement (Tableau 9) sont obtenues par application des probabilités de survie (Tableau 8) à la population dénombrée des femmes âgées de 10 à 64 ans, au moyen de l’équation 8.
Tableau 9 Nombre de femmes par groupe quinquennal d’âge 0, 5, 10 et 15 ans avant le recensement de 2008 au Cambodge
Groupe d’âge | 2008,17 | 2003,17 | 1998,17 | 1993,17 |
|---|---|---|---|---|
10-14 | 815 930 | 784 134 | 705 852 | 640 512 |
15-19 | 780 320 | 701 746 | 636 977 | 372 754 |
20-24 | 697 160 | 632 014 | 370 014 | 454 008 |
25-29 | 626 430 | 366 133 | 449 548 | 414 964 |
30-34 | 361 650 | 443 047 | 409 395 | 376 470 |
35-39 | 435 880 | 401 624 | 369 909 | 320 300 |
40-44 | 393 760 | 361 474 | 313 672 | 258 772 |
45-49 | 352 520 | 304 701 | 252 137 | 190 119 |
50-54 | 294 280 | 242 285 | 183 546 | |
55-59 | 230 200 | 173 224 | ||
60-64 | 160 590 |
L’interpolation linéaire entre les quatre colonnes de droite du tableau 9 permet d’estimer aisément la population par groupe d’âge quinquennal pour les 15 années centrées sur les dates 6, 18, 30 … 174 mois avant le recensement, c'est-à-dire en 2007,67 ; 2006,67 ; … ; 1993,67. Un extrait des résultats est présenté au tableau 10.
Tableau 10 Nombre de femmes par groupe quinquennal d’âge par année
Groupe d’âge | 2007,67 | 2006,67 | 2005,67 | 2004,67 | 2003,67 | 2002,67 |
|---|---|---|---|---|---|---|
10-14 | 812 750 | 806 391 | 800 032 | 793 672 | 787 313 | 776 305 |
15-19 | 772 463 | 756 748 | 741 033 | 725 318 | 709 604 | 695 269 |
20-24 | 690 645 | 677 616 | 664 587 | 651 558 | 638 528 | 605 814 |
25-29 | 600 400 | 548 341 | 496 281 | 444 222 | 392 162 | 374 474 |
30-34 | 369 790 | 386 069 | 402 349 | 418 628 | 434 907 | 439 682 |
35-39 | 432 454 | 425 603 | 418 752 | 411 901 | 405 050 | 398 453 |
40-44 | 390 531 | 384 074 | 377 617 | 371 160 | 364 703 | 356 694 |
45-49 | 347 738 | 338 174 | 328 610 | 319 046 | 309 483 | 299 444 |
Etape 3 : Calculer les taux globaux de fécondité
Les taux globaux de fécondité sont calculés grâce à l’équation 9, les naissances du tableau 7 et la population des femmes de 15-49 ans (Tableau 10).
Tableau 11 Estimations du taux global de fécondité (GFR), Cambodge 1993-2008
Milieu d’année | GFR (15-49) (pour mille) |
|---|---|
2007,67 | 82 |
2006,67 | 80 |
2005,67 | 85 |
2004,67 | 93 |
2003,67 | 94 |
2002,67 | 102 |
2001,67 | 106 |
2000,67 | 112 |
1999,67 | 121 |
1998,67 | 106 |
1997,67 | 134 |
1996,67 | 119 |
1995,67 | 156 |
1994,67 | 163 |
1993,67 | 168 |
Etape 4 : Estimer les taux par âge et l’indice synthétique de fécondité
Par interpolation linéaire entre les deux séries de taux de fécondité du tableau 5, on peut calculer les distributions de fécondité – pour un indice synthétique d’un enfant par femme – pour chacune des années précédant le recensement. Le tableau 12 donne un extrait de la série, illustrant une partie des calculs.
Tableau 12 Distributions de fécondité interpolées par groupe quinquennal d’âge et par année
Groupe d’âge | 2007,67 | 2006,67 | 2005,67 | 2004,67 | 2003,67 | 2002,67 |
|---|---|---|---|---|---|---|
10-14 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
15-19 | 0,0123 | 0,0126 | 0,0128 | 0,0131 | 0,0133 | 0,0136 |
20-24 | 0,0456 | 0,0465 | 0,0474 | 0,0483 | 0,0492 | 0,0502 |
25-29 | 0,0496 | 0,0500 | 0,0503 | 0,0506 | 0,0509 | 0,0513 |
30-34 | 0,0426 | 0,0423 | 0,0421 | 0,0418 | 0,0416 | 0,0413 |
35-39 | 0,0310 | 0,0304 | 0,0299 | 0,0293 | 0,0287 | 0,0282 |
40-44 | 0,0158 | 0,0153 | 0,0148 | 0,0143 | 0,0138 | 0,0133 |
45-49 | 0,0031 | 0,0029 | 0,0028 | 0,0026 | 0,0024 | 0,0022 |
Pour chaque année, la multiplication du nombre de femmes dans chaque groupe d’âge par la distribution de fécondité correspondante pour ce groupe d’âge indique ce que serait le nombre d’enfants dans ce groupe d’âge si l’indice synthétique de fécondité était égal à un enfant par femme.
Mais le nombre de naissances annuelles a déjà été estimé (Tableau 7). Le rapport entre ces estimations et celles faites dans l’hypothèse d’un indice synthétique égal à 1 représente l’estimation de l’indice synthétique de fécondité de chaque année.
Tableau 13 Estimations de l’indice synthétique de fécondité, Cambodge 1993-2007
Milieu d’année | Indice synthétique |
|---|---|
2007,67 | 2,76 |
2006,67 | 2,69 |
2005,67 | 2,85 |
2004,67 | 3,15 |
2003,67 | 3,18 |
2002,67 | 3,46 |
2001,67 | 3,56 |
2000,67 | 3,78 |
1999,67 | 4,09 |
1998,67 | 3,58 |
1997,67 | 4,48 |
1996,67 | 3,89 |
1995,67 | 4,98 |
1994,67 | 5,07 |
1993,67 | 5,10 |
Interprétation
Les résultats de l’application des méthodes de survie inverse aux données du recensement de 2008 au Cambodge sont représentés Figure 1. Le graphique fait apparaître clairement le recul de la fécondité au Cambodge au cours des 15 années antérieures à 2008. Alors que le taux de natalité estimé par la méthode 1 augmente légèrement entre deux périodes quinquennales avant le recensement, l’indice synthétique de fécondité recule continuellement. On voit aussi sur la figure 1 l’impact sur la structure par âge, et par conséquent sur les estimations de fécondité, d’une préférence pour la déclaration de certains âges : 8, 10 et 12, plutôt que 9 ou 11 ans.
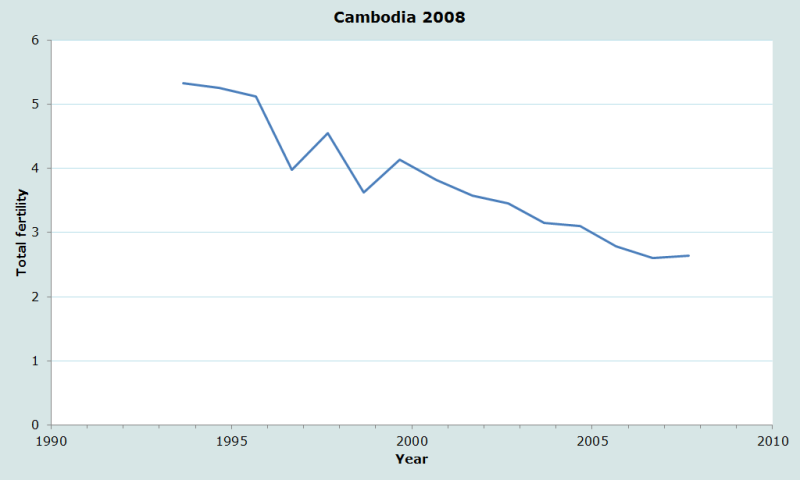
En général, les principales difficultés susceptibles de se produire lors de l’estimation de la fécondité par les méthodes de survie inverse ne proviennent ni de la procédure de projection rétrospective elle-même ni des hypothèses sur la distribution par âge de la fécondité, mais d’erreurs dans la déclaration des âges ou de l’omission par les répondants de certains jeunes enfants membres du ménage. Ces omissions et l’exagération des âges des jeunes enfants produisent souvent une fausse impression d’accélération de la baisse de la fécondité dans les quelques années précédant le recensement. Rien ne permet de penser que de telles erreurs de déclarations se sont produites au Cambodge.
Etant donné que dans la plupart des populations contemporaines les décès dans les quinze premières années de vie sont relativement rares, les erreurs dans les hypothèses sur la mortalité des enfants ont un impact modeste sur les estimations de fécondité. Une surestimation de la mortalité des enfants entraine une surestimation de la fécondité passée et réciproquement. Comme la proportion cumulée d’enfants décédés augmente au fil des âges, les erreurs sur la mortalité affectent davantage les estimations les plus anciennes et créent un léger biais dans les estimations de l’évolution de la fécondité. Il est souvent plus facile de déterminer s’il existe de tels biais quand on peut représenter plusieurs séries d’estimations de la fécondité sur un même graphique, plutôt qu’une seule comme on l’a fait ici.
Extensions de la méthode
La méthode mère-progéniture est une extension bien établie des méthodes de projection rétrospective pour estimer la fécondité. Une présentation complète de la méthode a été donnée par Cho, Retherford and Choe (1986). Elle conduit aussi à des estimations de l’indice synthétique de fécondité, mais au lieu de s’appuyer sur des estimations indépendantes de la distribution par âge de la fécondité pour répartir les naissances entre les mères elle cherche à relier chaque enfant recensé à sa mère. Ceci permet de classer les enfants à la fois selon leur âge et celui de leur mère. Ces effectifs peuvent ensuite être rétro-projetés pour déterminer le nombre d’enfants nés par année selon l’âge de leur mère à leur naissance.
Dans les enquêtes où des informations détaillées ont été recueillies sur les relations familiales au sein du ménage, et en particulier si un identifiant des mères qui vivent avec leurs enfants a été porté sur l’enregistrement de chaque enfant, un exercice d’appariement est possible, même s’il passe par un algorithme complexe. Des hypothèses sont nécessaires concernant l’âge des mères d’enfants adoptifs et des orphelins de mère et, s’ils sont nombreux, il peut être problématique de supposer qu’ils peuvent être répartis par groupe d’âge des mères au prorata (Timæus 2021).
Si l’information sur les relations au sein du ménage est sommaire, l’appariement des enfants et de leur mère peut devenir problématique, surtout dans les populations où les ménages regroupent souvent des familles étendues. En particulier, si la mère ne réside pas dans le ménage, les enfants risquent d’être rattachés à tort à une tante, une grand-mère ou une autre femme plutôt que de rester sans lien maternel. Ces erreurs ont généralement pour conséquence d’exagérer la fécondité estimée des femmes âgées. Les divorces, les remariages et les mariages polygames accroissent aussi le risque d’identifier à tort une femme comme mère d’un enfant.
Nous ne pouvons pas donner de conseil ici sur les algorithmes détaillés qu’il faudrait utiliser pour rattacher les enfants à leur mère quand on applique la méthode des enfants du ménage pour estimer la fécondité, car la procédure adoptée doit être exactement adaptée aux questions qui ont été posées et aux procédures de travail sur le terrain. Par exemple, l’appariement est plus aisé si on a demandé aux enquêteurs de lister ensemble les membres de chaque unité familiale restreinte, plutôt que de regrouper les membres du ménage par âge ou par genre.
Comme un nombre important de jeunes gens quittent le foyer à la fin de leur adolescence (y compris, dans la plupart des cultures, les jeunes femmes qui se marient), la recommandation de n’appliquer les méthodes de projection rétrospective qu’à l’estimation de la fécondité des 15 années précédant le recensement vaut à plus forte raison encore pour les estimations obtenues par la méthode des enfants du ménage.
Malgré ces éventuelles restrictions, l’expérience montre que la méthode mère-progéniture peut donner des estimations de fécondité de même qualité que celles calculées à partir de données d’histoire génésique. En fait, comme elles évitent le problème de troncature des taux de fécondité des femmes âgées à mesure que le estimations remontent dans le temps et comme les données d’histoire génésique doivent être recueillies auprès des femmes en personne et que celles qui ne peuvent pas être interrogées ont en moyenne une fécondité moindre que les autres, certains analystes pensent que les estimations produites par la méthode des enfants du ménage sont meilleures que les estimations directes tirées d’histoires génésiques dans la plupart des cas. (Avery, St. Clair, Levin et al. 2013)
Par ailleurs, les méthodes de projection rétrospective décrites ici en détail fonctionnent généralement bien au niveau national. Elles ne nécessitent pas un accès à des données individuelles et elles peuvent aboutir à des estimations plus précises que la méthode mère-progéniture dans les cas où les appariements erronés des enfants à leur mère sont fréquents.
La méthode mère-progéniture est cependant particulièrement appropriée pour les études de fécondité différentielle selon les caractéristiques de la mère comme son instruction, sa résidence ou son état matrimonial. Comme elle peut être appliquée à des données de recensement, la méthode peut permettre d’estimer la fécondité de sous-groupes trop peu nombreux pour être étudiés par des données d’enquête de fécondité. En outre, comme les informations sur les caractéristiques des femmes sont généralement beaucoup plus nombreuses dans les recensements que sur les bulletins de naissance, la méthode reste valable même dans les pays où l’enregistrement des naissances est complet.
Références
Avery C, T St. Clair, M Levin and K Hill. 2013. "The 'Own Children' fertility estimation procedure: A reappraisal", Population Studies 67(2): 171-183. https://dx.doi.org/10.1080/00324728.2013.769616
Brass W. 1979. "Evaluation of birth and death registration using age distributions and child survivorship data", Asian and Pacific Census Forum 5(3):9-11,20. https://hdl.handle.net/10125/3563
Cho LJ, RD Retherford and MK Choe. 1986. The Own-Child Method of Fertility Estimation. Honolulu: University of Hawaii Press.
Division de la Population des Nations Unies. 1984. Manuel X. Techniques indirectes d’estimation démographique. New York : Nations Unies, Département des affaires économiques et sociales internationales, ST/ESA/SER.A/81. https://unstats.un.org/unsd/demographic/standmeth/handbooks/Manuel_X-fr.pdf
Timæus IM. 2021. "The Own-Children Method of fertility estimation: The devil is in the detail", Demographic Research 45: 825-840. https:/dx.doi.org/10.4054/DemRes.2021.45.25
- Printer-friendly version
- Log in to post comments
